数据结构之链表与递归

1、提起链表，有一块非常重要的内容，就是递归，这是因为链表本身具有天然的递归性，同时，链表也是一种结构非常简单的数据结构，使得链表是一种非常好的来学习和研究递归这种逻辑机制的数据结构。

2、使用一个简单的案例，数组求和，使用递归算法进行计算。案例，如下所示：

 1 package com.array;
 2 
 3 /**
 4  * 数组求和，使用递归算法进行计算。
 5  * 

 6  * 递归算法的基本原则。
 7  * 1、第一部分，求解最基本的问题。
 8  * 例如，return 0;递归算法就是将原问题变成了一个更小的问题，
 9  * 更小的问题变成一个更更小的问题，以此类推，直到变成了一个最基本的问题，这个最基本的问题是不能自动求解的，
10  * 是需要我们编写逻辑进行求解的。这里对数组求和的算法就表现在if (left == arr.length) { return 0;}，先判断
11  * 一下，我们当前真的是一个最基本的问题，是的话，直接返回retun 0;
12  * 2、第二部分，把原问题转化成更小的问题的这样一个过程。
13  * 通常，对于递归算法来说，最基本的问题都是极其简单的，甚至基本上都是这样的一种形式，直接return一个数就行了。
14  * 最基本的问题，一眼就可以看出答案是多少了，但是难得是如何把原问题转化成更小的问题呢，所谓的转化为更小的问题，
15  * 不是求一个更小的问题的答案就好了，是根据更小的问题的答案构建出原问题的答案。
16  * 这里面的构建就是让arr[left] + 更小的一段数组中所有的元素的和，那么，这个构建方式非常简单。
17  */
18 public class ArraySum {
19 
20     /**
21      * 数组求和，用户调用的公开方法。
22      *
23      * @param arr
24      * @return
25      */
26     public static int sum(int[] arr) {
27         // 思路，一点一点缩小数组的大小，就是，数组从那里一直到数组的最后对数组进行求和。这些规模在一直减小。
28         // 调用私有的sum方法，将数组arr传入参数1，索引0位置传入参数2。
29         // 参数2传入的是0，是递归的初始调用，计算的是从0一直到n-1这些元素所有的和。
30         return sum(arr, 0);
31     }
32 
33     /**
34      * 递归算法，对用户屏蔽的私有方法。
35      * 

36      * 私有的函数，计算arr[left...n)这个区间内所有数字的和。即left到n-1这些索引区间的和。
37      *
38      * @param arr  数组
39      * @param left 左边界的点，其实是一个索引
40      * @return
41      */
42     private static int sum(int[] arr, int left) {
43         // 首先判断，left等于数组长度的时候，说明递归到了最后
44         if (left == arr.length) {
45             // 此时，整个数组为空的时候，直接返回0即可
46             return 0;
47         } else {
48             // 否则，返回arr[left] + sum(arr, left + 1)。
49             // 取出，现在要计算出从left到n-1这些索引的所有元素的和。
50             // 把左边的元素单独拿出来，就是arr[left]，再加上sum，对arr的从left + 1这个索引，一直到n-1这个索引。
51             // 这些范围里面的所有元素进行求和操作。sum(arr, left + 1)就是递归调用的过程。
52             return arr[left] + sum(arr, left + 1);
53             // 我们计算从left到n这个区间范围内的所有元素的和，变成了计算从left+1到n所有数字的和。
54             // 我们解决的这个问题，规模变小了，直到最终left和数组的长度相等的时候，也就是要求一个空数组的和。
55         }
56     }
57 
58     public static void main(String[] args) {
59         int[] arr = new int[]{1, 2, 3, 4, 5, 6, 7, 8, 9};
60         int sum = ArraySum.sum(arr);
61         System.out.println("数组之和： " + sum);
62     }
63 
64 }

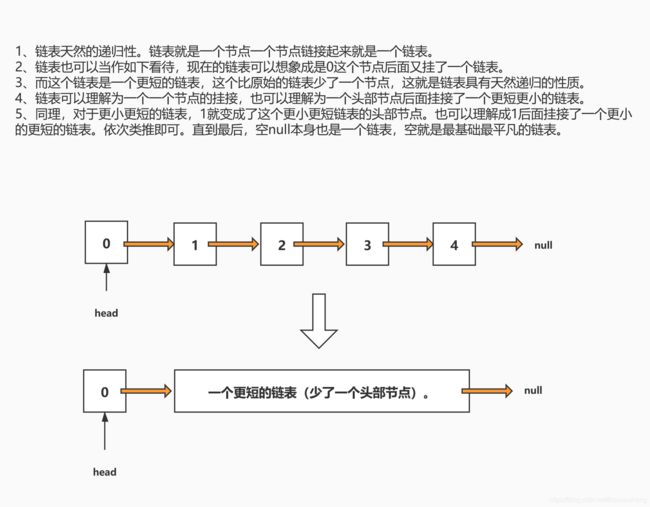
3、链表天然的递归性。链表就是一个节点一个节点链接起来就是一个链表。链表也可以当作如下看待，现在的链表可以想象成是0这个节点后面又挂了一个链表。

4、使用链表递归解决，删除链表中等于给定值val的所有节点。

实现代码，如下所示：

 1 package com.leetcode;
 2 
 3 /**
 4  * 删除链表中等于给定值 val 的所有节点。
 5  * 

 6  * Definition for singly-linked list.
 7  * 

 8  * public class ListNode {
 9  * int val;
10  * ListNode next;
11  * ListNode(int x) { val = x; }
12  * }
13  */
14 public class RemoveLinkedList3 {
15 
16     /**
17      * 删除链表中等于给定值 val 的所有节点。
18      * 输入: 1->2->6->3->4->5->6, val = 6
19      * 输出: 1->2->3->4->5
20      *
21      * @param head
22      * @param val
23      * @return
24      */
25     public ListNode removeElements(ListNode head, int val) {
26         // 使用链表的递归解决删除链表中等于给定值 val 的所有节点。
27         // 对于递归的解决，只有两个部分。
28         // 第一个部分，就是对于那种最基本的情况，也就是问题规模最小的那种情况，它的解是什么。
29         // 头部节点后面跟着一个小的短的链表，走到最底的情况，就是链表的头部节点head等于空。也就是整个链表为空。
30         if (head == null) {
31             // 此时，不需要任何逻辑。
32             return head;// 此时，return返回head还是return null都是一样的。
33         }
34 
35         // 第二部分，把原问题转化成更小的问题的这样一个过程。
36         // 知道removeElements这个函数，这个模块，把它当作一个子模块，它的宏观语意，
37         // 它做的事情就是对一个链表中删除掉值为val这样的的节点。
38         // 所以对head接的这个链表中值为val的节点进行删除即可。
39 //        ListNode removeElements = removeElements(head.next, val);
40 
41         // 也可以写成如下写法，让返回值直接存储到head的下一个节点中。
42         head.next = removeElements(head.next, val);
43         // removeElements存储的就是应该是我们将头节点后面跟的那个链表中所有的值为val的节点删除后剩余的节点。
44         // removeElements就是将指定的val删除掉以后剩余的节点。
45 
46         // 写法一
47         // 此时，进行处理，head这个节点的值是怎么样的。
48 //        if (head.val == val) {
49 //            // 如果此时，head这个节点的值是待删除的val值。此时，把head节点删除了，
50 //            // removeElements存储的就是head之后跟的那个链表，完成了这个任务之后，得到的结果给它返回。
51 //            return removeElements;
52 //        } else {
53 //            // 让head的下一个节点指向了removeElements这个节点。将head节点连接到最前面。
54 //            // head节点后面跟head后面的那个链表删除了val之后得到的那个结果的链表给它接上。
55 //            head.next = removeElements;
56 //            return head;
57 //        }
58 
59 
60         // 写法二
61 //        if (head.val == val) {
62 //            // 如果此时，head这个节点的值是待删除的val值。此时，把head节点删除了，
63 //            // removeElements存储的就是head之后跟的那个链表，完成了这个任务之后，得到的结果给它返回。
64 //            return head.next;
65 //        } else {
66 //            // 让head的下一个节点指向了removeElements这个节点。将head节点连接到最前面。
67 //            // head节点后面跟head后面的那个链表删除了val之后得到的那个结果的链表给它接上。
68 //            return head;
69 //        }
70 
71         // 写法三
72         // 直接写成三目运算符，更加方便。
73         return head.val == val ? head.next : head;
74     }
75 
76 
77     public static void main(String[] args) {
78         int[] arr = new int[]{1, 2, 6, 3, 4, 5, 6};
79         // 创建ListNode
80         ListNode head = new ListNode(arr);
81         // 打印head，注意，这里的head虽然是一个头部节点，但是覆盖了toString方法，这里的head是以head作为头部节点的整个链表对应的字符串。
82         System.out.println(head);
83         // 创建本来对象
84         RemoveLinkedList3 removeLinkedList = new RemoveLinkedList3();
85         // 调用方法，删除待删除元素的节点
86         ListNode removeElements = removeLinkedList.removeElements(head, 6);
87         // 打印输出即可
88         System.out.println(removeElements);
89     }
90 
91 }

5、递归函数的微观解读。递归函数的调用，本质就是函数调用，和普通函数的调用没有区别，只不过调用的函数是自己而已。

5.1、数组求和，使用递归算法进行计算。递归调用的函数微观解读。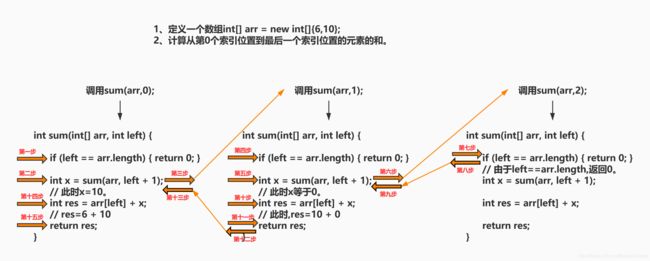

5.2、使用链表递归解决，删除链表中等于给定值val的所有节点，微观层面的步骤解析。

总结，递归调用是有代价的，函数调用（需要时间的开销，需要记录当前的逻辑执行到那里了，当前的局部变量都是怎么样的）+  系统栈空间（递归调用消耗系统栈的空间的）。

6、递归算法的调试，可以根据打印输出或者开发工具的debug进行调试即可。

  1 package com.company.linkedlist;
  2 
  3 /**
  4  * @ProjectName: dataConstruct
  5  * @Package: com.company.linkedlist
  6  * @ClassName: RemoveLinkedList
  7  * @Author: biehl
  8  * @Description: ${description}
  9  * @Date: 2020/3/9 9:48
 10  * @Version: 1.0
 11  */
 12 public class RemoveLinkedList {
 13 
 14     // 内部类
 15     class ListNode {
 16 
 17         int val;
 18         ListNode next;
 19 
 20         ListNode(int x) {
 21             val = x;
 22         }
 23 
 24         /**
 25          * 将数组转换为链表结构
 26          * 

 27          * 链表节点的构造函数，使用arr为参数，创建一个链表，当前的ListNode为链表头节点。
 28          * 

 29          * 将整个链表创建完成以后，这个构造函数是一个节点的构造函数，我们最终呢，
 30          * 相当于把我们的当前构造的这个节点作为头节点。
 31          *
 32          * @param arr
 33          */
 34         public ListNode(int[] arr) {
 35             // 首先，判断数组arr是否合法，数组不能为空，必须包含元素
 36             if (arr == null || arr.length == 0) {
 37                 throw new IllegalArgumentException("arr can not be empty.");
 38             }
 39 
 40             // 让数组索引为0的元素即第一个元素赋值给存储链表节点元素的val。
 41             this.val = arr[0];
 42             // 遍历数组，将数组中的每一个元素都创建成新的ListNode节点。链接到前一个节点上，形成这样的一个链表。
 43             // 创建一个节点，从this开始，将之后的节点都链接到此节点的后面。
 44             ListNode current = this;
 45             for (int i = 1; i < arr.length; i++) {
 46                 // 让从this开始，将之后的节点都链接到此节点的后面。
 47                 current.next = new ListNode(arr[i]);
 48                 // 让current这个几点。每次循环都向后移动一个位置，将后面的节点都依次进行挂接。
 49                 current = current.next;
 50             }
 51             // 最后，this就是我们用上面的循环创建的链表相对应的头部节点head。
 52         }
 53 
 54         /**
 55          * 为了方便在main函数中观察链表。
 56          * 

 57          * 返回的是以当前节点为头部节点的链表信息字符串。
 58          * 

 59          * 注意，这里的ListNode是一个节点哈，不是一个链表结构。
 60          *
 61          * @return
 62          */
 63         @Override
 64         public String toString() {
 65             StringBuilder stringBuilder = new StringBuilder();
 66             // 从自身开始循环
 67             ListNode current = this;
 68             // 循环遍历，只要current不为空，就进行操作
 69             while (current != null) {
 70                 // 将当前节点的val值进行拼接
 71                 stringBuilder.append(current.val + "->");
 72                 // 将current向下一个节点进行移动
 73                 current = current.next;
 74             }
 75             // 表示达到了链表的尾部。
 76             stringBuilder.append("NULL");
 77             return stringBuilder.toString();
 78         }
 79     }
 80 
 81     /**
 82      * 根据递归深度生成一个深度字符串。
 83      *
 84      * @param depth
 85      * @return
 86      */
 87     private String generateDepthString(int depth) {
 88         StringBuilder stringBuilder = new StringBuilder();
 89         for (int i = 0; i < depth; i++) {
 90             // 每次循环添加两个中划线，方便观察递归效果。深度越深，中划线越多。
 91             stringBuilder.append("--");
 92         }
 93         return stringBuilder.toString();
 94     }
 95 
 96 
 97     /**
 98      * @param head  以head为头部节点的链表。
 99      * @param val   待删除元素。
100      * @param depth 递归深度，每一个函数在内部调用一次自己，可以理解为递归深度多了一。
101      *              递归深度帮助理解递归的一个变量。
102      * @return
103      */
104     public ListNode removeElements(ListNode head, int val, int depth) {
105         // 根据递归深度生成一个深度字符串。
106         String depthString = generateDepthString(depth);
107         // 首先打印一下深度字符串。打印的是在这个递归深度下。
108         System.out.print(depthString);
109         // 复用了ListNode的toString方法。表示，在head为头部节点的链表删除val这个元素。
110         System.out.println("Call: remove " + val + " in " + head);
111 
112         if (head == null) {
113             System.out.print(depthString);
114             System.out.println("Return: " + head);
115             // 此时，不需要任何逻辑。
116             return head;// 此时，return返回head还是return null都是一样的。
117         }
118 
119         // 也可以写成如下写法，让返回值直接存储到head的下一个节点中。递归深度每次加一。
120         ListNode res = removeElements(head.next, val, depth + 1);
121         System.out.print(depthString);
122         System.out.println("After: remove " + val + " : " + res);
123 
124         ListNode ret;
125         if (head.val == val) {
126             // 删除头部节点
127             ret = res;
128         } else {
129             // 不删除头部节点
130             head.next = res;
131             ret = head;
132         }
133         System.out.print(depthString);
134         System.out.println("Return: " + res);
135 
136         return ret;
137     }
138 
139 
140     public static void main(String[] args) {
141         int[] arr = new int[]{1, 2, 6, 3, 4, 5, 6};
142         // 创建ListNode
143         ListNode head = new RemoveLinkedList().new ListNode(arr);
144         // 打印head，注意，这里的head虽然是一个头部节点，但是覆盖了toString方法，这里的head是以head作为头部节点的整个链表对应的字符串。
145         System.out.println(head);
146         // 创建本来对象
147         RemoveLinkedList removeLinkedList = new RemoveLinkedList();
148         // 调用方法，删除待删除元素的节点。递归深度，默认是0
149         ListNode removeElements = removeLinkedList.removeElements(head, 6, 0);
150         // 打印输出即可
151         System.out.println(removeElements);
152     }
153 
154 }

运行效果，如下所示：

7、关于递归，链表具有天然的递归结构，近乎和链表相关的所有操作，都可以使用递归的形式来完成，比如，可以使用递归对链表进行增加，删除，修改和查询操作的。

7.1、双链表的结构。

7.2、循环链表的结构。

7.3、数组链表的结构。