图论算法(6)：LeetCode 图论算法练习（785.判断二分图、695.岛屿的最大面积、Floodfill 算法、并查集）

本章节内容使用 java 实现，Github 代码仓：https://github.com/ZhekaiLi/Code/tree/main/Graph/src

查看文章内的图片可能需要科学上网！ 因为使用了github管理图片，因此如果出现无法加载的情况请

【参考资料】imooc 波波老师：玩转算法系列–图论精讲 面试升职必备（Java版）

【往期博客链接】
图论算法(1、2)：图的分类、图的基本概念（无向图与有向图、无权图、无环图、完全图、二分图；简单图、连通分量、图的生成树、子图与母图）
图论算法(3)：图的基本表示（邻接矩阵、邻接表、邻接矩阵与邻接表的对比）
图论算法(4)：图的深度优先遍历 DFS
图论算法(5)：图的广度优先遍历 BFS
图论算法(6)：LeetCode 图论算法练习（785.判断二分图、695.岛屿的最大面积、Floodfill 算法、并查集）

6 LeetCode 图论算法练习

785. 判断二分图

可以参考 Section 4.4

java 实现：LeetCode785_me.java（作者使用了BFS）

695. 岛屿的最大面积

该问题的核心为图的建模，也就是从题目所给的二维数组中提取点、边的信息。我们的目标是把如下矩阵

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

转化成

// AdjList[i] 储存结点i的邻接点
AdjList = [[1, 4, 8], [2, 7, 9], ...]

但传统邻接表内结点的表示为整数，而在题干矩阵中，结点则以二维位置参数表示，主要步骤如下：
（1）将结点信息由二维映射至一维

（2）判断任一结点是否存在相邻点

（3）根据之前写的求解无向图联通分量的算法，完成代码主体

可以参考 Section 4.1

java 实现 v1：LeetCode695_me.java（LeetCode 上显示我击败了5.3%的用户…，好垃圾。可能是使用了一些相对复杂的数据结构，但是在逻辑方面我个人感觉还是挺OK的）
java 实现 v2：LeetCode695.java（更好的代码示例）
先将二维矩阵转化为 HashSet 类型的图信息，再使用 dfs。核心代码：

private int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}}; // 四连通

private HashSet<Integer>[] constructGraph(){
    HashSet<Integer>[] g = new HashSet[R * C];
    for (int i = 0; i < g.length; i++)
        g[i] = new HashSet<>();

    for (int v = 0; v < g.length; v++) {
        int x = v / C, y = v % C; // 将一维信息转化为二维坐标
        if (grid[x][y] == 1) {
            for (int d = 0; d < 4; d++) {
                int nextx = x + dirs[d][0], nexty = y + dirs[d][1];
                if (inArea(nextx, nexty) && grid[nextx][nexty] == 1){
                    int next = nextx * C + nexty;
                    g[v].add(next);
                }}}}
    return g;
}

private int dfs(int v){
    visited[v] = true;
    int res = 1;
    for(int w: G[v]){
        if(!visited[w])
            res += dfs(w);
    }
    return res;
}

java 实现 v3：LeetCode695_plus.java
直接使用输入的二维矩阵来保存图信息，改造 dfs 使之适用于二维输入。核心代码：

private int dfs(int x, int y){
    visited[x][y] = true;
    int res = 1;
    for(int d = 0; d < 4; d++){
        int nextx = x + dirs[d][0], nexty = y + dirs[d][1];
        if(inArea(nextx, nexty) && !visited[nextx][nexty] && grid[nextx][nexty] == 1)
            res += dfs(nextx, nexty);
    }
    return res;
}

6.1 floodfill 算法

上一个小节的最后一段代码（java 实现 v3）也被称之为 floodfill 算法，本质上与 dfs 相同，只不过将原本的根据边来传播的方式，更改为在坐标系内向的四个方向的传播。图例如下：

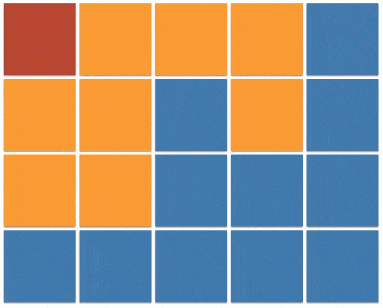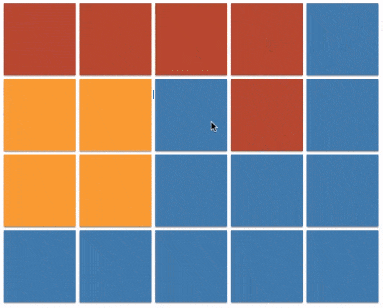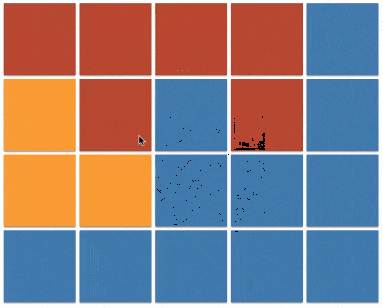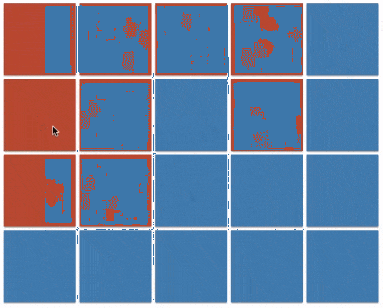
floodfill 的应用

ps里边的魔棒、扫雷游戏

LeetCode 中的相关问题

200. 岛屿的数量
1020. 飞地的数量
130. 被围绕的区域
733. 图像渲染（floodfill）
1034. 边框着色
529. 扫雷游戏
827. 最大人工岛屿 [Hard]

6.2 连通性和并查集

class UF{
    private int[] parent;

    public UF(int n){
        parent = new int[n];
        for(int i = 0 ; i < n ; i ++)
            parent[i] = i;
    }

    public int find(int p){
        if( p != parent[p] )
            parent[p] = find( parent[p] );
        return parent[p];
    }

    public boolean isConnected(int p , int q){
        return find(p) == find(q);
    }

    public void unionElements(int p, int q){
        int pRoot = find(p);
        int qRoot = find(q);
        if( pRoot == qRoot )
            return;
        parent[pRoot] = qRoot;
    }
}

以下将以图 + 代码结合的方式展示并查集的创建、运行过程：

UF uf = new UF(6);

uf.unionElements(2, 1);
uf.unionElements(3, 1);
uf.unionElements(5, 4);
uf.unionElements(6, 4);

uf.unionElements(4, 1);

需要注意的是函数 find(int p)，该函数在每次运行的时候不仅仅能返回结点p的根节点，还将结点p的父结点直接改成其根结点。这样的功能实现能够避免出现长长一大串的连接

更进一步的，我们可以改进 UF 类，使之支持查找任意一元素所在集合的元素个数

class UF{
    private int[] parent;
    private int[] sz; // 1. 我们需要一个 sz 数组，存储以第 i 个元素为根节点的集合的元素个数。

    public UF(int n){
        parent = new int[n];
        sz = new int[n];
        for(int i = 0 ; i < n ; i ++){
            parent[i] = i;
            sz[i] = 1; // 2. 初始化，每个 sz[i] = 1
        }
    }

    public int find(int p){ // 没有变化... }
    public boolean isConnected(int p , int q){ // 没有变化 }

    public void unionElements(int p, int q){
        int pRoot = find(p);
        int qRoot = find(q);
        if( pRoot == qRoot )
            return;
        parent[pRoot] = qRoot;
        // 3. 维护 sz：把 qRoot 的集合元素数量加上 pRoot 的集合元素数量
        sz[qRoot] += sz[pRoot];
    }

    // 4. 最后，设计一个接口让用户可以查询到任意一个元素 p 所在的集合的元素个数 
    public int size(int p){
        return sz[find(p)]; // 使用 p 所在的集合的根节点查找相应的元素个数
    }
}

使用 floodfill + 并查集的 LeetCode 练习

695. 岛屿的最大面积