数据结构与算法——列表排序(一篇文章带你了解排序算法)
数据结构与算法基础
列表排序:
什么是列表排序?
排序:将一组“无序”的记录序列调整为“有序”的记录序列。
列表排序:将无序列表变为有序列表。
内置函数:sort();
常见排序算法的介绍:
1、冒泡排序;
2、选择排序;
3、插入排序;
4、快速排序;
5、堆排序;
6、归并排序;
7、希尔排序;
8、计数排序;
9、基数排序;
排序算法分析:
冒泡排序:列表每两个相邻的数,如果前面比后面大,则交换这两个数。分为两个区一个叫有序区,一个叫无序区。
一趟排序完成后,无序区减少一个数,有序区增加一个数。
冒泡排序针对无序区; 运行n-1趟;
无序区的范围:n-i-1
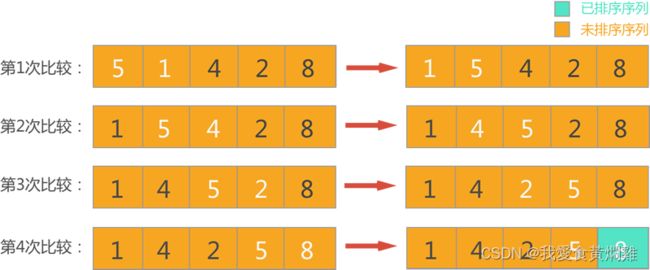
代码如下:
def dubble_sort(li):
for i in range(len(li)-1):#第i躺
for j in range(len(li)-i-1):#无序区指的趟数
if li[j]>li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
print(li)
li = [3,1,4,2,7,6,5]
print(li)
dubble_sort(li)
冒泡排序的时间复杂度:O(n^2)
计算机目的:求快
一趟过程中,无序区已经没有发生交换了,使用标志位。
改进代码:
def dubble_sort(li):
for i in range(len(li)-1):#第i躺
exchange = False
for j in range(len(li)-i-1):#无序区指的趟数
if li[j]>li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
exchange = True
print(li)
if not exchange:
return
#冒泡内容到此结束了
选择排序: 一趟排序记录最小的数,放到第一个位置,再一趟排序记录列表无序区最小的数,放到第二个位子。
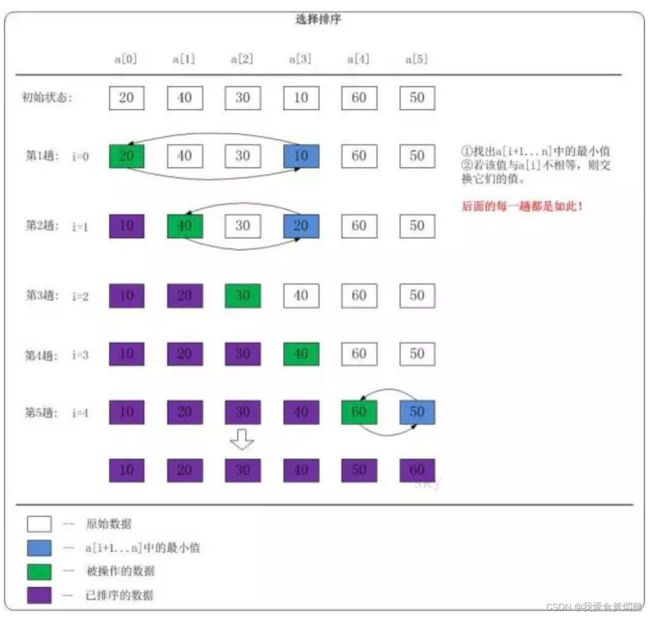
代码如下:
def selcet_sort_simple(li):
li_new = []
for i in range(len(li)):
min_val = min(li)
li_new.append(min_val)
li.remove(min_val)
return li_new
但由于时间复杂度为O(n^3),所以引进改进方法。
代码:
def selecet_sort(li):
for i in range(len(li)-1): # i 为第i躺
min_val = i
for j in range(i+1,len(li)):
if li[j]<li[min_val]:
li[j],li[min_val] = li[min_val],li[j]
print(li)
#选择排序到此结束
插入排序: 怎么插比较准呢?
可以以摸牌的形式来理解,初始时手里只有一张牌,每次从无序区摸一张牌,插入到手里已有牌的正确位置。
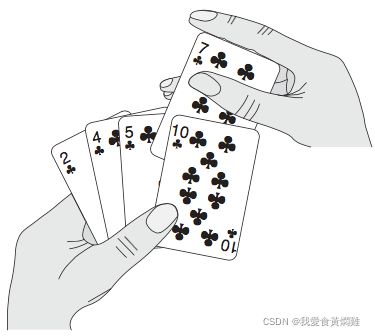
代码如下:
def insert_sort(li):
for i in range(1,len(li)):#表示摸到牌的下标
j = i -1 #j指的是手里牌的下标
temp = li[i]
while j>=0 and li[j]>temp :
li[j+1] = li[j]
j = j -1;
li[j+1] = temp
#插入排序到此结束
快速排序: 快速排序就是一个字快!
快速排序思路:取一个元素a(第一个元素),使用元素a归位。
列表被a分成两部分,左边都比a小,右边都比a大;最后递归完成排序。
快速排序的时间复杂度:O(nlogn)。
最坏情况时间复杂度:O(n^2)。
递归是很消耗系统资源的
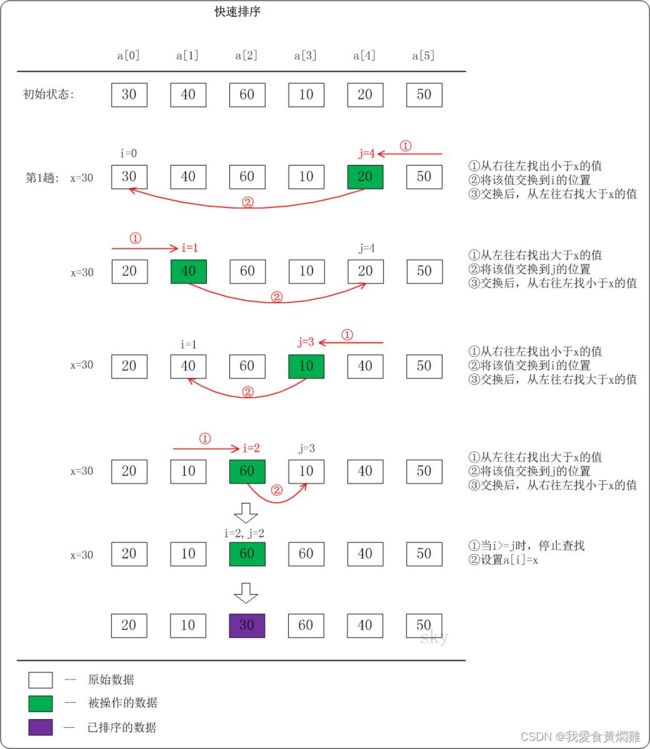
代码如下:
def quick_sort(data,left,right):
if left < right:
mid = partition(data,left,right)
quick_sort(data,left,mid-1)
quick_sort(data,mid+1,right)
def partition(li,left,right):
temp = li[left]
while left < right:
while left < right and li[right] >= temp: #从右面找到比temp小的数
right = right - 1 #往左走一步
li[left] = li[right] #把右边的值写到左边空位上
while left < right and li[left] <= temp:
left = left + 1
li[right] = li[left]
li[left] = temp #把temp归位
#快速排序到此结束
堆排序(最难): 堆:一种特殊的完全二叉树结构,可分为大根堆和小根堆(得先去了解树的基础才能理解)。
大根堆:一棵完全二叉树,满足任一节点都比其孩子大。
小根堆:一棵完全二叉树,满足任一节点都比其孩子小。
堆排序——向下调整(当根节点的左右子树都是堆时,可以通过一次向下的调整来将其变成一个堆)。
堆排序过程:
1、建立堆。
2、得到堆顶元素,为最大元素。
3、去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调整重新使堆有序。
4、堆顶元素为第二大元素。
5.、重复步骤3,直到堆变空。
堆排序的时间复杂度:O(nlogn)

代码如下:
def sift(li,low,high):
"""
:param li:列表
:param low: 堆的根节点位置
:param high: 堆的最后一个元素的位置
:return:
"""
i = low #i最开始指向的根节点
j = 2 * i + 1 #j开始是左孩子
tmp = li[low] #堆顶存起来
while j <= high :#只要j位置有数
if j +1 <= high and li[j+1] > li[j]: #如果右孩子有且比较大
j = j + 1 #指向右孩子
if li[j] > tmp:
li[i] = li[j]
i = j #往下看一层
j = 2*i + 1
else: #tmp更大,把tmp放在i的位置上
li[i] = tmp #把tmp放到某一级领导位置上
break
else:
li[i] = tmp
def heap_sort(li):
n = len(li)
for i in range((n-2)//2,-1,-1):
sift(li,i,len(li)-1)#建堆完成
for i in range(len(li)-1,-1,-1):#i 指向当前堆的最后一个元素
li[0], li[i] = li[i], li[0]
sift(li,0,i-1) #i-1是新的high
#堆排序到此结束
归并排序: 两段有序列表,合成为一个有序列表,这种操作称为一次归并。
假设有一段无序列表又该怎么使用归并排序呢?
分解:将列表越分越小,直至分成一个元素。
终止条件:一个元素是有序的。
合并:将两个有序列表归并,列表越来越大。
归并排序的时间复杂度:O(nlogn)
归并排序的空间复杂度:O(n)
因为归并排序不像之前排序一样是原地排序,需要额外的内存开销,所以需要空间复杂度!
如图所示:
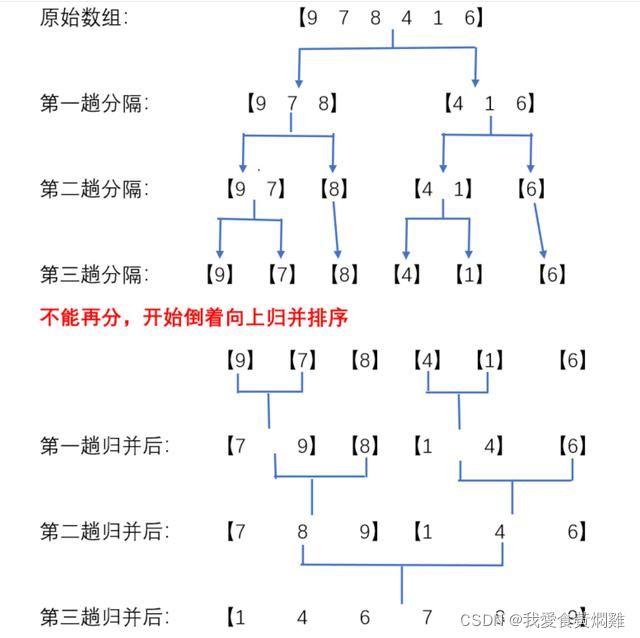
可以使用递归思想去理解,代码如下:
def merge(li,low,mid,high):
i = low
j = mid + 1
ltmp = []
while i <= mid and j <= high:#只要左右两边都有数
if li[i] < li[j]:
ltmp.append(li[i])
i = i + 1
else:
ltmp.append(li[j])
j = j + 1
while i <= mid: #当右边没数时
ltmp.append(li[i])
i = i + 1
while j <= high:#当左边没数时
ltmp.append(li[j])
j = j+1
li[low:high+1] = ltmp
def merge_sort(li,low,high):
if low < high: #至少有两个元素
mid = (low + high)//2
merge_sort(li,low,mid)
merge_sort(li,mid+1,high)
merge(li,low,mid,high
#理解可以参考汉诺塔问题
#归并排序到此结束
希尔排序: 希尔排序是一种分组插入排序算法
n为列表长度
首先取一个整数d1 = n/2,将元素分为d1个组,每组相邻量元素之间距离为d1,在各组内进行插入排序;
取第二个整数d2 = d1/2,重复上述分组排序过程,直到
d1 = 1,即所有元素在同一组内进行直接插入排序。
希尔排序每趟并不使某些元素有序,而是使整体数据越来约接近有序,最后一趟排序使得所有数据有序。
希尔排序的时间复杂度与gap的选取有关
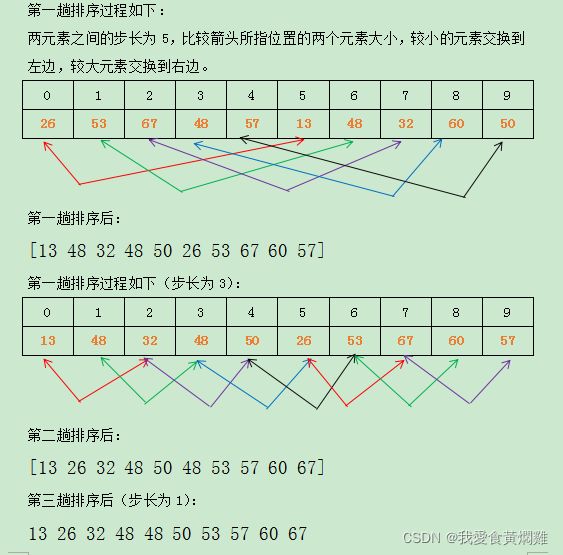
代码如下:
def insert_sort(li,gap):
for i in range(gap,len(li)):#表示摸到牌的下标
j = i - gap #j指的是手里牌的下标
temp = li[i]
while j>=0 and li[j]>temp :
li[j+gap] = li[j]
j = j -gap;
li[j+gap] = temp
def shell_sort(li):
d = len(li) // 2
while d >= 1:
insert_sort(li,d)
d //= 2
#原理与插入排序类似,理解了插入排序,希尔排序也能理解
#希尔排序到此结束
计数排序: 对列表进行排序,已知列表中的范围都在0到100之间。
计数排序的时间复杂度为:O(n)
代码如下:
def count_sort(li,max_count = 100):
count = [0 for _ in range(max_count+1)]
for val in li:
count[val] +=1
li.clear()
for ind ,val in enumerate(count):
for i in range(val):
li.append(ind)
#计数排序到此结束
桶排序: 首先将元素分在不同的桶中,在对每个桶中的元素排序。
桶排序的表现取决于数据的分布。也就是需要对不同数据排序时采取不同的分桶策略。
桶排序的时间复杂度:O(n+k)
桶排序的空间复杂度:O(nk)
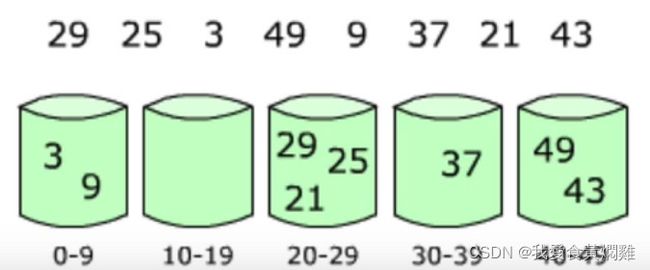 代码如下:
代码如下:
def bucket_sort(li, n=100,max_num=10000):
buckets =[[]for _ in range(n)]
for var in li:
i = min(var // (max_num//n),n-1) #表示var放在几号桶里
buckets[i].appends(var)
#保持桶内是顺序
for j in range(len(buckets[i])-1,0,-1):
if buckets[i][j] < buckets[i][j-1]:
buckets[i][j],buckets[i][j-1] = buckets[i][j-1],buckets[i][j]
else:
break
sorted_li = []
for buc in buckets:
sorted_li.extend(buc)
return sorted_li
#桶排序就到此结束
基数排序: 基数排序是一种借助“多关键字排序”的思想来实现“单关键字排序”的内部排序算法。根据键值的每位数字来分配桶;
def redix_sort(li):
max_num = max(li)
it = 0
while 10 ** it <= max_num:
buckets = [[] for _ in range(10)]
for var in li:
digit = (var // 10 **it)%10
buckets[digit].append(var)
li.clear()
for buc in buckets:
li.extend(buc)
it +=1
#该代码主要还是利用了桶的思想
#基数排序到此结束
