深度学习库PyTorch（附代码）

转自：数据派THU ID：DatapiTHU

原文标题：

An Introduction to PyTorch – A Simple yet Powerful Deep LearningLibrary

作者：FAIZAN SHAIKH

翻译：和中华

本文约3600字，建议阅读15分钟。
本文通过案例带你一步步上手PyTorch。

  

介绍

每隔一段时间，就会有一个有潜力改变深度学习格局的python库诞生，PyTorch就是其中一员。

 

在过去的几周里，我一直沉浸在PyTorch中，我被它的易用性所吸引。在我使用过的各种深度学习库中，到目前为止PyTorch是最灵活最易用的。

在本文中，我们将以一种更实用的方式探索PyTorch, 其中包含了基础知识和案例研究。同时我们还将对比分别用numpy和PyTorch从头构建的神经网络，以查看它们在具体实现中的相似之处。

 

让我们开始吧！

 

注意：本文假定你对深度学习有基本的认知。如果想快速了解，请先阅读此文https://www.analyticsvidhya.com/blog/2016/03/introduction-deep-learning-fundamentals-neural-networks/

 

目录

• PyTorch概览

• 深入技术

• 构建神经网络之Numpy VS. PyTorch

• 与其他深度学习库对比

• 案例研究 --- 用PyTorch解决图像识别问题

 

PyTorch概览

PyTorch的创作者说他们遵从指令式(imperative)的编程哲学。这就意味着我们可以立即运行计算。这一点正好符合Python的编程方法学，因为我们没必要等到代码全部写完才知道它是否能运行。我们可以轻松地运行一部分代码并实时检查它。对于我这样的神经网络调试人员而言，这真是一件幸事。

 

PyTorch是一个基于python的库，它旨在提供一个灵活的深度学习开发平台。

PyTorch的工作流程尽可能接近Python的科学计算库--- numpy。

 

你可能会问，我们为什么要用PyTorch来构建深度学习模型呢？我列举三点来回答这个问题：

 

• 易用的API：像Python一样简单易用；

• 支持Python：如上所说，PyTorch平滑地与Python数据科学栈集成。它与Numpy如此相似，你甚至都不会注意到其中的差异；

• 动态计算图：PyTorch没有提供具有特定功能的预定义图，而是提供给我们一个框架用于构建计算图，我们甚至可以在运行时更改它们。这对于一些情况是很有用的，比如我们在创建一个神经网络时事先并不清楚需要多少内存。

 

使用PyTorch还有其他一些好处，比如它支持多GPU，自定义数据加载器和简化的预处理器。

 

自从2016年1月初发布以来，许多研究人员已经将它纳入自己的工具箱，因为它易于构建新颖甚至非常复杂的图。话虽如此，PyTorch要想被大多数数据科学从业者所接受还需时日，因为它既是新生事物而且还在”建设中”。

 

深入技术

在深入细节之前，我们先了解一下PyTorch的工作流程。

 

PyTorch使用了指令式编程范式。也就是说，用于构建图所需的每行代码都定义了该图的一个组件。即使在图被完全构建好之前，我们也可以在这些组件上独立地执行计算。这被称为 ”define-by-run” 方法。

 

Source: http://pytorch.org/about/

 

安装PyTorch非常简单。你可以根据你的系统，按照官方文档中提到的步骤操作。例如，下面是基于我的选项所用的命令：

 

conda install pytorch torchvision cuda91 -cpytorch

 

在我们开始使用PyTorch时，应该了解的主要元素是：

 

• PyTorch张量(Tensors)

• 数学运算

• Autograd模块

• Optim模块

• nn模块

 

下面，我们将详细介绍每一部分。

 

1. PyTorch张量

张量就是多维数组。PyTorch中的张量与Numpy中的ndarrays很相似，除此之外，PyTorch中的张量还可以在GPU上使用。PyTorch支持各种类型的张量。

 

你可以定义一个简单的一维矩阵如下：

 

# import pytorch

import torch

# define a tensor

torch.FloatTensor([2])

 

2

[torch.FloatTensor of size 1]

 

2. 数学运算

与numpy一样，科学计算库有效地实现数学函数是非常重要的。PyTorch提供了一个类似的接口，你可以使用超过200多种数学运算。

 

以下是一个简单的加法操作例子：

 

a = torch.FloatTensor([2])

b = torch.FloatTensor([3])

a + b

5

[torch.FloatTensor of size 1]

 

这难道不像是一个典型的python方法吗？我们也可以在定义过的PyTorch张量上执行各种矩阵运算。例如，我们转置一个二维矩阵：

 

matrix = torch.randn(3, 3)

matrix

-1.3531 -0.5394  0.8934

 1.7457 -0.6291 -0.0484

-1.3502 -0.6439 -1.5652

[torch.FloatTensor of size 3x3]

matrix.t()

-1.3531  1.7457  -1.3502

-0.5394 -0.6291  -0.6439

 0.8934  -0.0484  -1.5652

[torch.FloatTensor of size 3x3]

 

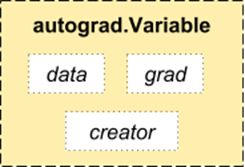
3. Autograd模块

 

PyTorch使用了一种被称为自动微分(automaticdifferentiation)的技术。也就是说，我们有一个记录器，记录了我们已经执行的操作，然后它向后重播以计算我们的梯度。这种技术在构建神经网络时特别有用，因为我们在前向传播时计算参数的微分，这可以减少每一个epoch的计算时间。

 

Source: http://pytorch.org/about/

 

from torch.autograd import Variable

x = Variable(train_x)

y = Variable(train_y, requires_grad=False)

 

4. Optim模块

Torch.optim是一个模块，它实现了用于构建神经网络的各种优化算法。大多数常用的方法已被支持，所以我们无需从头开始构建他们（除非你想！）。

 

以下是使用Adam优化器的一段代码：

 

optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

5. nn模块

PyTorch的autograd可以很容易的定义计算图并且求梯度，但是原始的autograd对于定义复杂的神经网络可能有点过于低级。这也是nn模块可以帮忙的地方。

 

Nn包定义了一组模块，我们可以将其视为一个神经网络层，它可以从输入产生输出，并且可能有一些可训练的权重。

 

你可以把nn模块当做是PyTorch的keras!

 

import torch

# define model

model = torch.nn.Sequential(

 torch.nn.Linear(input_num_units, hidden_num_units),

 torch.nn.ReLU(),

 torch.nn.Linear(hidden_num_units, output_num_units),

)

loss_fn = torch.nn.CrossEntropyLoss()

 

现在你知道了PyTorch的基本组件，你可以轻松地从头构建自己的神经网络。如果你想知道具体怎么做，继续往下读。

 

构建神经网络之 Numpy VS. PyTorch

之前我提到PyTorch和Numpy非常相似，让我们看看为什么。在本节中，我们会看到一个简单的用于解决二元分类问题的神经网络如何实现。你可以通过https://www.analyticsvidhya.com/blog/2017/05/neural-network-from-scratch-in-python-and-r/获得深入的解释。

 

## Neural network in numpy

import numpy as np

#Input array

X=np.array([[1,0,1,0],[1,0,1,1],[0,1,0,1]])

#Output

y=np.array([[1],[1],[0]])

#Sigmoid Function

def sigmoid (x):

 return 1/(1 + np.exp(-x))

#Derivative of Sigmoid Function

def derivatives_sigmoid(x):

 return x * (1 - x)

#Variable initialization

epoch=5000 #Setting training iterations

lr=0.1 #Setting learning rate

inputlayer_neurons = X.shape[1] #number of features in data set

hiddenlayer_neurons = 3 #number of hidden layers neurons

output_neurons = 1 #number of neurons at output layer

#weight and bias initialization

wh=np.random.uniform(size=(inputlayer_neurons,hiddenlayer_neurons))

bh=np.random.uniform(size=(1,hiddenlayer_neurons))

wout=np.random.uniform(size=(hiddenlayer_neurons,output_neurons))

bout=np.random.uniform(size=(1,output_neurons))

for i in range(epoch):

  #Forward Propogation

  hidden_layer_input1=np.dot(X,wh)

  hidden_layer_input=hidden_layer_input1 + bh

  hiddenlayer_activations = sigmoid(hidden_layer_input)

  output_layer_input1=np.dot(hiddenlayer_activations,wout)

  output_layer_input= output_layer_input1+ bout

  output = sigmoid(output_layer_input)

  #Backpropagation

  E = y-output

  slope_output_layer = derivatives_sigmoid(output)

  slope_hidden_layer = derivatives_sigmoid(hiddenlayer_activations)

  d_output = E * slope_output_layer

  Error_at_hidden_layer = d_output.dot(wout.T)

  d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer

  wout += hiddenlayer_activations.T.dot(d_output) *lr

  bout += np.sum(d_output, axis=0,keepdims=True) *lr

  wh += X.T.dot(d_hiddenlayer) *lr

  bh += np.sum(d_hiddenlayer, axis=0,keepdims=True) *lr

print('actual :\n', y, '\n')

print('predicted :\n', output)

 

现在，尝试发现PyTorch超级简单的实现与之前的差异（下面代码中差异部分用粗体字表示）。

 

## neural network in pytorch

import torch

#Input array

X = torch.Tensor([[1,0,1,0],[1,0,1,1],[0,1,0,1]])

#Output

y = torch.Tensor([[1],[1],[0]])

#Sigmoid Function

def sigmoid (x):

  return 1/(1 + torch.exp(-x))

#Derivative of Sigmoid Function

def derivatives_sigmoid(x):

  return x * (1 - x)

#Variable initialization

epoch=5000 #Setting training iterations

lr=0.1 #Setting learning rate

inputlayer_neurons = X.shape[1] #number of features in data set

hiddenlayer_neurons = 3 #number of hidden layers neurons

output_neurons = 1 #number of neurons at output layer

#weight and bias initialization

wh=torch.randn(inputlayer_neurons, hiddenlayer_neurons).type(torch.FloatTensor)

bh=torch.randn(1, hiddenlayer_neurons).type(torch.FloatTensor)

wout=torch.randn(hiddenlayer_neurons, output_neurons)

bout=torch.randn(1, output_neurons)

for i in range(epoch):

  #Forward Propogation

  hidden_layer_input1 = torch.mm(X, wh)

  hidden_layer_input = hidden_layer_input1 + bh

  hidden_layer_activations = sigmoid(hidden_layer_input)

  output_layer_input1 = torch.mm(hidden_layer_activations, wout)

  output_layer_input = output_layer_input1 + bout

  output = sigmoid(output_layer_input1)

  #Backpropagation

  E = y-output

  slope_output_layer = derivatives_sigmoid(output)

  slope_hidden_layer = derivatives_sigmoid(hidden_layer_activations)

  d_output = E * slope_output_layer

  Error_at_hidden_layer = torch.mm(d_output, wout.t())

  d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer

  wout += torch.mm(hidden_layer_activations.t(), d_output) *lr

  bout += d_output.sum() *lr

  wh += torch.mm(X.t(), d_hiddenlayer) *lr

  bh += d_output.sum() *lr

print('actual :\n', y, '\n')

print('predicted :\n', output)

 

• 与其他深度学习库对比

在一个基准测试脚本中，通过比较最低的epoch中位数时间，PyTorch在训练一个Long Short Term Memory(LSTM)网络方面胜过了所有其他主要的深度学习库，参加下图：

 

用于数据加载的APIs在PyTorch中设计良好。接口在数据集，采样器和数据加载器中指定。

 

在比较TensorFlow中的数据加载工具(readers, queues等等)时，我发现PyTorch的数据加载模块非常易于使用。另外，PyTorch在我们尝试构建神经网络时是无缝衔接的，所以我们不必像keras那样依赖第三方高级库（keras依赖tensorflow或theano）。

 

另一方面，我不推荐使用PyTorch进行部署。 PyTorch尚处于发展中。正如PyTorch开发人员所说：“我们看到的是用户首先创建一个PyTorch模型，当他们准备将模型部署到生产环境时，他们只需将其转换成Caffe 2模型，然后将其发布到移动平台或其他平台。“

案例研究：用PyTorch解决图像识别问题

为了熟悉PyTorch，我们将解决Analytics Vidhya的深度学习实践问题 - 识别数字。我们来看看我们的问题陈述：

 

我们的问题是一个图像识别问题，从一个给定的28×28像素的图像中识别数字。我们有一部分图像用于训练，其余部分用于测试我们的模型。

 

首先，下载训练和测试文件。该数据集包含所有图像的压缩文件，并且train.csv和test.csv都具有相应训练和测试图像的名称。数据集中不提供任何其他特征，只是以'.png'格式提供原始图像。

 

让我们开始吧：

 

步骤0：准备

1. 导入所有必要的库：

# import modules

%pylab inline

import os

import numpy as np

import pandas as pd

from scipy.misc import imread

from sklearn.metrics import accuracy_score

 

2. 设置种子值，以便我们可以控制模型的随机性

# To stop potential randomness

seed = 128

rng = np.random.RandomState(seed)

3. 第一步是设置目录路径，以便安全保存！

root_dir = os.path.abspath('.')

data_dir = os.path.join(root_dir, 'data')

# check for existence

os.path.exists(root_dir), os.path.exists(data_dir)

 

步骤1：数据加载和预处理

1. 现在我们来读取数据集。他们是.csv格式，并且具有相应标签的文件名。

 

# load dataset

train = pd.read_csv(os.path.join(data_dir, 'Train', 'train.csv'))

test = pd.read_csv(os.path.join(data_dir, 'Test.csv'))

sample_submission = pd.read_csv(os.path.join(data_dir, 'Sample_Submission.csv'))

train.head()

 

2. 我们看一下数据是什么样子，读取图片并显示。

# print an image

img_name = rng.choice(train.filename)

filepath = os.path.join(data_dir, 'Train', 'Images', 'train', img_name)

img = imread(filepath, flatten=True)

pylab.imshow(img, cmap='gray')

pylab.axis('off')

pylab.show()

3. 为了便于数据操作，我们将所有图片存储为numpy数组。

 

# load images to create train and test set

temp = []

for img_name in train.filename:

  image_path = os.path.join(data_dir, 'Train', 'Images', 'train', img_name)

  img = imread(image_path, flatten=True)

  img = img.astype('float32')

  temp.append(img)

train_x = np.stack(temp)

train_x /= 255.0

train_x = train_x.reshape(-1, 784).astype('float32')

temp = []

for img_name in test.filename:

  image_path = os.path.join(data_dir, 'Train', 'Images', 'test', img_name)

  img = imread(image_path, flatten=True)

  img = img.astype('float32')

  temp.append(img)

test_x = np.stack(temp)

test_x /= 255.0

test_x = test_x.reshape(-1, 784).astype('float32')

train_y = train.label.values

 

4. 由于这是一个典型的ML问题，为了测试我们模型的正确功能，我们创建了一个验证集(validation set)。我们以70:30的比例来划分训练集和验证集。

 

# create validation set

split_size = int(train_x.shape[0]*0.7)

train_x, val_x = train_x[:split_size], train_x[split_size:]

train_y, val_y = train_y[:split_size], train_y[split_size:]

 

步骤2：构建模型

5. 现在来到了主要部分，即定义我们的神经网络架构。我们定义了一个3层神经网络即输入，隐藏和输出层。输入和输出层中的神经元数量是固定的，因为输入是我们的28×28图像，并且输出是代表类别的10×1向量。我们在隐藏层中使用50个神经元。在这里，我们使用Adam作为优化算法，它是梯度下降算法的有效变种。

 

import torch

from torch.autograd import Variable

# number of neurons in each layer

input_num_units = 28*28

hidden_num_units = 500

output_num_units = 10

# set remaining variables

epochs = 5

batch_size = 128

learning_rate = 0.001

6. 训练模型的时间到了

 

# define model

model = torch.nn.Sequential(

  torch.nn.Linear(input_num_units, hidden_num_units),

  torch.nn.ReLU(),

  torch.nn.Linear(hidden_num_units, output_num_units),

)

loss_fn = torch.nn.CrossEntropyLoss()

# define optimization algorithm

optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

## helper functions

# preprocess a batch of dataset

def preproc(unclean_batch_x):

  """Convert values to range 0-1"""

  temp_batch = unclean_batch_x / unclean_batch_x.max()

  return temp_batch

# create a batch

def batch_creator(batch_size):

  dataset_name = 'train'

  dataset_length = train_x.shape[0]

  batch_mask = rng.choice(dataset_length, batch_size)

  batch_x = eval(dataset_name + '_x')[batch_mask]

  batch_x = preproc(batch_x)

  if dataset_name == 'train':

    batch_y = eval(dataset_name).ix[batch_mask, 'label'].values

  return batch_x, batch_y

# train network

total_batch = int(train.shape[0]/batch_size)

for epoch in range(epochs):

  avg_cost = 0

  for i in range(total_batch):

    # create batch

    batch_x, batch_y = batch_creator(batch_size)

    # pass that batch for training

    x, y = Variable(torch.from_numpy(batch_x)), Variable(torch.from_numpy(batch_y), requires_grad=False)

    pred = model(x)

    # get loss

    loss = loss_fn(pred, y)

    # perform backpropagation

    loss.backward()

    optimizer.step()

    avg_cost += loss.data[0]/total_batch

  print(epoch, avg_cost)

# get training accuracy

x, y = Variable(torch.from_numpy(preproc(train_x))), Variable(torch.from_numpy(train_y), requires_grad=False)

pred = model(x)

final_pred = np.argmax(pred.data.numpy(), axis=1)

accuracy_score(train_y, final_pred)

# get validation accuracy

x, y = Variable(torch.from_numpy(preproc(val_x))), Variable(torch.from_numpy(val_y), requires_grad=False)

pred = model(x)

final_pred = np.argmax(pred.data.numpy(), axis=1)

accuracy_score(val_y, final_pred)

训练得分是：

0.8779008746355685

而验证得分是：

0.867482993197279

这是一个很令人印象深刻的分数，尤其是我们只是在5个epochs上训练了一个非常简单的神经网络。

结语

我希望这篇文章能让你看到PyTorch如何改变构建深度学习模型的观点。在这篇文章中，我们只是浅尝辄止。为了深入研究，你可以阅读PyTorch官方页面上的文档和教程。

在接下来的几篇文章中，我将使用PyTorch进行音频分析，并且我们将尝试构建语音处理的深度学习模型。敬请关注！

你用过PyTorch构建应用程序或者将其用在任何数据科学项目里吗？请在下面的评论中告诉我。

原文链接：

https://www.analyticsvidhya.com/blog/2018/02/pytorch-tutorial/