- 工控一体机具体有哪些作用?
工控一体机作为一种集成了计算机硬件、输入输出设备以及工业控制软件的工业控制计算机,其在工业自动化、智能制造及其他多个领域具有重要的作用。以下是工控一体机的具体作用:一、数据采集与监控实时数据采集:工控一体机能够连接各种传感器和检测设备,实时采集生产现场的温度、压力、流量、速度等参数数据。数据监控与显示:通过其集成的显示屏和触摸屏,工控一体机能够以图形化、直观化的方式显示采集到的数据,方便操作人员实
- R语言开发记录,一
[email protected]
R语言r语言开发语言
1.清理环境rm(list=ls())gc()rm(list=ls())作用:删除当前R工作环境中所有的对象(变量、函数、数据框等)。解释:ls():列出当前环境中所有对象的名字。list=ls():将这些名字作为一个列表传给rm()函数。rm():移除这些对象。效果:相当于“清空内存”,让工作空间恢复到干净状态。gc()作用:手动触发垃圾回收(garbagecollection)。效果:释放R不
- 嵌入式Linux-线程同步-自旋锁和读写锁
线程同步一、自旋锁1.1自旋锁概述1.2自旋锁的初始化1.3自旋锁加锁和解锁二、读写锁2.1何为读写锁2.2读写函数初始化2.3读写锁上锁和解锁2.4读写锁的属性一、自旋锁1.1自旋锁概述自旋锁与互斥锁很相似,从本质上说也是一把锁,在访问共享资源之前对自旋锁进行上锁,在访问完成后释放自旋锁(解锁);事实上,从实现方式上来说,互斥锁是基于自旋锁来实现的,所以自旋锁相较于互斥锁更加底层。如果在获取自旋
- Android阴影效果的艺术与实现:从入门到精通
大模型大数据攻城狮
android安卓动画canvaspaintandroid阴影安卓面试android面经
目录1.阴影的本质:为什么它对UI如此重要?2.深入MaterialDesign:理解Z轴与阴影层次3.兼容老版本:用Drawable实现阴影4.高级技巧:自定义OutlineProvider5.用Canvas绘制自定义阴影:解锁无限可能6.阴影性能优化:让丝滑体验飞起来7.JetpackCompose中的阴影实现:拥抱现代化8.动态阴影动画:打造炫酷交互效果9.RecyclerView中的阴影实
- 每日一题 2025-7-6 《努力的乐乐》
WYC135164
算法
K14363努力的乐乐题目描述乐乐的数学成绩在班级里很拔尖,但是语文成绩一直不太好,所以他在这个学期一开始就一直很努力学习语文。这个学期乐乐一共参加了n次考试,他现在想统计下这n次考试中,自己的语文成绩和数学成绩之间的差距有没有缩小。现在给出乐乐这n次考试每一次的两科成绩,请你帮助他算一下每一次数学成绩减去语文成绩的差值。输入格式第一行,一个正整数n,表示乐乐参加的考试次数。接下来n行,每行两个正
- AtCoder Beginner Contest 412(ABCDE)
前言回来喽!!前一阵子期末周快复习疯了,接下来还想准备数学建模,感觉高中都没这么忙过T^T。中间参加了一场百度之星的比赛,只AC了两题,感觉好难啊还是太菜了,希望能混个牌呜呜呜。图论和数论题好难,还得多练啊……一、A-TaskFailedSuccessfully#includeusingnamespacestd;typedeflonglongll;typedefpairpii;voidsolve(
- 『 Linux 』线程安全的单例模式,自旋锁与读写锁
Dio夹心小面包
线程LinuxC++linux单例模式javascript服务器c++运维
文章目录单例模式懒汉模式与饿汉模式自旋锁读写锁单例模式单例模式是一种创建型设计模式,其主要目的是确保一个类只有一个实例,并提供一个全局访问点来访问该实例;这在需要严格控制如何及合适访问某个唯一资源型下有一定作用;单利模式的主要特点为如下:私有构造函数单例模式通常要将构造私有化,以保证无法直接通过该类实例化出对应的对象;只能通过该类提供对应的接口来实例化整个对象,确保只有一个实例;私有静态实例私有静
- DM 数据库概述
2301_82150492
数据库
目录DM数据库概述安装DM数据库实例配置详解备份与还原策略DM数据库函数运用SQL查询语句实战DMSQL程序设计总结与展望引言达梦数据库(DM)是一款国产的高性能数据库管理系统,具有丰富的功能和良好的兼容性,广泛应用于各类企业级应用场景。它支持多种操作系统,如Windows、Linux等,并提供了完善的数据库管理工具和开发接口。安装DM数据库系统准备在安装DM数据库之前,需要确保目标系统满足一定的
- WHAT - React Native 中 Light and Dark mode 深色模式(黑暗模式)机制
文章目录一、Light/DarkMode的原理1.操作系统层2.ReactNative如何获取?3.样式怎么跟着变?二、关键代码示例讲解代码讲解:三、自定义主题四、运行时自动更新五、核心原理一张图组件应用例子最小示例:动态样式按钮的动态样式如何封装一套自定义主题四、如何和ThemeProvider配合?小技巧总结总结一句话这其实是现代移动应用开发中非常常用的功能:自动适配浅色/深色模式(Light
- 【Python】类(class)的创建
Herbert_JL
pythonpythonlinux
1类简介1.1什么是类在面向对象编程(OOP)中,类(Class)是一种封装了数据和操作这些数据的函数的编程结构。它是一种抽象的概念,用于定义具有相同属性(变量)和方法(函数)的对象的模板。类可以看作是一个“蓝图”,用于创建具有相同特征和行为的对象实例。1.2类的作用1.2.1封装(Encapsulation)类将数据(属性)和操作数据的方法封装在一起,形成一个独立的单元。这样可以隐藏内部实现细节
- 在python中function啥类型_Python中function和method
这两个概念已经有很多人解释过了,从本文的『参考』中就可以看出来。之所以还要写一篇这个主题,主要是为了用自己的语言表述一下,并且尽可能的讲的清楚一点。泛泛地说,function是一般意义上的函数,即对一段代码的封装,并由一个地址(函数名)来调用。method通常是面向对象的概念,即method是属于一个类或类的对象的。method是与类或类的对象相关的函数。下面讲一下我对这两个概念的更具体的理解。如
- 物联网零售领域AI算力网络与通信的应用探索
AI算力网络与通信
物联网零售人工智能ai
物联网零售领域AI算力网络与通信的应用探索关键词:物联网、零售领域、AI算力网络、通信、应用探索摘要:本文聚焦于物联网零售领域,深入探讨了AI算力网络与通信的应用。首先介绍了相关背景,包括目的、预期读者等。接着对核心概念进行解释,阐述它们之间的关系并给出原理架构示意图和流程图。然后详细讲解核心算法原理、数学模型与公式,通过项目实战展示代码案例及解读。还介绍了实际应用场景、推荐相关工具资源,分析未来
- 【华为od刷题(C++)】HJ30 字符串合并处理
m0_64866459
华为odc++链表
我的代码:#include//用于输入输出流#include//用于字符串处理#include//用于动态数组的处理#include//包含排序等常见算法#include//用于字符串流的处理,可以将数据从字符串流中提取#include//提供字符处理函数,如isdigit、isalpha等#include//提供位集处理,能够将数字转换为二进制表示usingnamespacestd;charbi
- ESP32 PWM开发对比:底层驱动 VS Arduino封装,谁更适合你?
小_楠_天_问
嵌入式硬件Arduinoesp32esp32-s3单片机PWM底层开发ESP-IDF
ESP32PWM开发对比:底层驱动VSArduino封装,谁更适合你?在ESP32的开发中,我们常常需要通过PWM(脉宽调制)控制LED灯的亮度、马达速度、蜂鸣器音调等。本篇文章将通过一个具体案例——呼吸灯效果,深入对比底层驱动方式(ESP-IDF原生API)与Arduino封装函数方式,帮助你理解它们之间的差异与各自适用的场景。我之前使用的是Arduino封装进行的PWM开发,但发现esp32开
- Dockerfile设置时区alpine
背景:最近在写golang相关代码。其中用到了时间操作的相关函数,如下:nowTime:=time.Now()nUnixEndTime:=nowTime.Unix()nHour,nMin,nSec:=nowTime.Clock()但代码跑在docker容器中,时间就取不对了。原因为容器中的时区与本机时区不一致。处理:设置docker容器的时区,Dockerfile如下设置:FROMalpineLA
- java面试题60JQuery选择器
码农颜
java开发语言
jQuery选择器是jQuery的核心功能之一,它允许你高效、简洁地查找和选取HTML文档中的元素。其语法基于CSS选择器,并进行了扩展,使其更加强大和灵活。使用$()函数(或jQuery()函数)来应用选择器。核心语法$(selector)selector:一个字符串,用于指定要查找哪些元素。主要类型及示例基本选择器(最常用):#id(ID选择器):选取具有指定ID的元素。$("#myEleme
- 结合创新idea:机器学习+运筹优化=CCF高端局
Ai多利
机器学习人工智能
2024深度学习发论文&模型涨点之——机器学习+运筹优化机器学习是人工智能的一个分支,它使计算机系统能够从数据中学习并改进其性能,而无需进行明确的编程。运筹优化,也称为运筹学或运营管理,是应用数学的一个分支,它使用数学模型和算法来支持复杂决策过程的制定。机器学习与运筹优化的结合是一个前沿且活跃的研究领域,它们相互补充,为解决复杂问题提供了新的思路和方法。小编整理了一些机器学习+运筹优化【论文+代码
- STM32的 syscalls.c 和 sysmem.c
is0815
stm32c语言嵌入式硬件
syscalls.c是STM32CubeIDE自动生成的标准系统调用适配文件,用于裸机环境下支持newlib标准库(如printf,scanf,malloc)的运行。这份文件提供了标准库运行所需的最小系统调用实现。现在我来逐段解析其作用,并补充你可能需要修改或关注的地方。主要用途该文件让标准C库函数在没有操作系统的STM32环境中可以正常工作。特别是:printf()调用_write()(需要重定
- 在 .docx 中键入正确的数学符号
文章目录\not\perp...做项目需要使用.docx写复杂的数学公式。虽然Word和WPS都已经支持LaTex代码,但是支持的很差劲(╬ ̄皿 ̄),许多符号无法生成。\not\perp为了输入⊥̸\not\perp⊥符号,需要依次执行:插入-符号字体:CambriaMath插入Unicode+22A5(⊥\perp⊥符号)插入Unicode+0338(⋅̸\not\sdot⋅组合符号)…
- 常见手撕项目C++
氏族归来
c++开发语言
常见手撕项目C++设计模式单例模式饿汉模式懒汉模式策略模式策略接口实现具体的策略(虚函数重写)定义上下文用户调用代码最短路径算法使用函数模板写冒泡排序写一个类模板stringreplace详解方法概览参数介绍代码示例多线程信号量解释设计模式单例模式单例模式是一种常用的软件设计模式,其目的是确保一个类只有一个实例,并提供一个全局访问点来获取该实例。优点:资源控制:单例模式能够确保一个类只有一个实例存
- LaTex 写演示文稿 - Beamer 入门 之 彩色文本框
joefsong
LaTeX学习笔记latex
Beamer入门之彩色文本框创建彩色文本框tcolorbox宏包使用技巧及文本框简元素介绍更改彩色文本框外观样式预定义样式标题字体字号标题颜色位置字体位置标题框位置正文边框边框形状方法一:边框变直角方法二:标题框下移边框颜色边框外观附录代码及拓展:本节内容给大家分享如何绘制彩色表格,大致的效果如下:该节的内容主要包括(链接可跳至B站视频链接):创建简单彩色文本框更改彩色文本框样式最终效果如下:创建
- 【GitHub开源项目实战】Agent-Zero 多模态 Agent 框架的架构实现与实战落地
观熵
GitHub开源项目实战github开源架构
开源项目实战解析:Agent-Zero多模态Agent框架的架构实现与实战落地关键词:Agent-Zero、LLMAgent、多模态融合、LangGraph、结构化对话、函数调用、RAG、真实场景实战、开源项目分析摘要:Agent-Zero是一个以LangGraph为核心构建的多模态智能体框架,专注于大语言模型(LLMs)驱动下的多模态Agent系统实现,具备高度模块化、支持结构化对话状态流转、工
- 【刚考完的真题】2025年全国青少年信息素养大赛—图形化编程挑战赛-复赛/省赛真题(小高组)——谢尔宾斯基地毯
部分地区的信息素养大赛图形化复赛已考完,还没考的小伙伴可以去做做,看看难度如何~谢尔宾斯基地毯谢尔宾斯基是波兰的一名数学家,他发现了一种“自相似”的图形——谢尔宾斯基地毯,构造方法如下:(1)取一个实心的正方形(2)将其划分为9个相等的小正方形(3)移除中间的小正方形,留下周围的8个小正方形(4)对这8个小正方形重复上述操作,每次迭代都会让结构变得更加复杂。具体要求对画笔进行编程,不要对画笔的初始
- <script setup>中的setup作用以及和不带的区别对比
在Vue3中,setup函数是CompositionAPI的核心入口,其作用与“不带setup”(即传统OptionsAPI)的区别主要体现在代码组织、复用性、类型支持等方面。以下是具体分析:一、setup的作用初始化响应式状态在setup中,可以通过ref和reactive创建响应式数据,替代OptionsAPI中的data选项[1][3]。示例:setup(){constcount=ref(0
- 【动态规划】一次性整理子序列问题题型系列,八个例题实战详细解析 (包含我自己精心整理的动态规划解题思路)
ngioig
动态规划leetcode算法职场和发展后端
前言最近刷了子序列系列的题型,一共八个力扣题,这里对子序列问题进行一个简单的总结,全是动态规划的解法,当然里边有些题选有更优的解法。1.动态规划解题思路动态规划(DynamicProgramming,DP)是一种在计算机科学和数学中用于解决最优化问题的方法。它特别适用于可以分解为互相重叠的子问题的问题,并且这些子问题的解可以被存储起来以避免重复计算,从而提高效率。首先,我们要熟悉动态规划的套路也要
- happy-llm 第二章 Transformer架构
weixin_38374194
transformer深度学习人工智能学习
文章目录一、注意力机制核心解析1.1注意力机制的本质与核心变量1.2注意力机制的数学推导1.3注意力机制的变种实现1.3.1自注意力(Self-Attention)1.3.2掩码自注意力(MaskedSelf-Attention)1.3.3多头注意力(Multi-HeadAttention)二、Encoder-Decoder架构详解2.1Seq2Seq任务与架构设计2.2核心组件解析2.2.1前馈
- JavaScript 函数
晚夜微雨问海棠呀
JavaScript教程javascript开发语言ecmascript
JavaScript函数是代码执行的基本单元,具有灵活的定义方式和强大的功能特性。以下是核心要点:一、定义方式类型语法特性函数声明functionfn(){...}存在变量提升,可在定义前调用函数表达式constfn=function(){...}无变量提升,需先定义后调用箭头函数constfn=()=>{...}无this、arguments,不能作为构造函数构造函数newFunction('a
- LabVIEW MathScript薄板热流模拟
LabVIEW开发
LabVIEW参考程序LabVIEW知识LabVIEW知识LabVIEW程序LabVIEW功能labview
热流模拟是热设计关键环节,传统工具精准但开发周期长,本VI利用LabVIEW优势,面向工程师快速验证需求,在初步方案迭代、教学演示等场景更具效率,为热分析提供轻量化替代路径,后续可结合专业工具,先通过本VI快速定性分析,再用传统工具精准求解,提升研发流程效率。此VI用于模拟单点热源下薄板的热流,求解带周期边界条件的椭圆型偏微分方程,借助LabVIEWMathScriptNode实现自定义函数,结合
- SQL注入与防御-第三章:复查代码中的SQL注入
复查代码中的SQL注入一、核心逻辑通过静态/动态代码分析,识别代码中直接拼接用户输入、未验证过滤的危险编码行为,定位“将用户可控数据传入SQL执行函数”的风险点,从代码源头预防SQL注入。核心是识别“用户输入→危险函数→SQL执行”的未净化链路,结合多场景适配,切断注入风险。二、关键步骤与方法(一)代码分析方法1.静态代码分析原理:不执行代码,直接审计源码,查找“用户输入拼接SQL”的危险逻辑。重
- Python基础——变量和数据类型
全端工程师
python基础python开发语言
Python基础——变量和数据类型前言一、什么是变量1.1为什么需要变量1.2变量的基本概念1.3变量的命名规则二、数据类型2.1什么是数据类型2.2使用`type()`函数2.3使用不同的数据类型三、类型转换3.1类型转换的基本概念3.2类型转换函数(显示类型转换)3.3隐式类型转换3.4类型转换的注意事项四、变量的使用五、总结前言今天我们开始学习Python编程的基础——变量和数据类型。这些概
- VMware Workstation 11 或者 VMware Player 7安装MAC OS X 10.10 Yosemite
iwindyforest
vmwaremac os10.10workstationplayer
最近尝试了下VMware下安装MacOS 系统,
安装过程中发现网上可供参考的文章都是VMware Workstation 10以下, MacOS X 10.9以下的文章,
只能提供大概的思路, 但是实际安装起来由于版本问题, 走了不少弯路, 所以我尝试写以下总结, 希望能给有兴趣安装OSX的人提供一点帮助。
写在前面的话:
其实安装好后发现, 由于我的th
- 关于《基于模型驱动的B/S在线开发平台》源代码开源的疑虑?
deathwknight
JavaScriptjava框架
本人从学习Java开发到现在已有10年整,从一个要自学 java买成javascript的小菜鸟,成长为只会java和javascript语言的老菜鸟(个人邮箱:
[email protected])
一路走来,跌跌撞撞。用自己的三年多业余时间,瞎搞一个小东西(基于模型驱动的B/S在线开发平台,非MVC框架、非代码生成)。希望与大家一起分享,同时有许些疑虑,希望有人可以交流下
平台
- 如何把maven项目转成web项目
Kai_Ge
mavenMyEclipse
创建Web工程,使用eclipse ee创建maven web工程 1.右键项目,选择Project Facets,点击Convert to faceted from 2.更改Dynamic Web Module的Version为2.5.(3.0为Java7的,Tomcat6不支持). 如果提示错误,可能需要在Java Compiler设置Compiler compl
- 主管???
Array_06
工作
转载:http://www.blogjava.net/fastzch/archive/2010/11/25/339054.html
很久以前跟同事参加的培训,同事整理得很详细,必须得转!
前段时间,公司有组织中高阶主管及其培养干部进行了为期三天的管理训练培训。三天的课程下来,虽然内容较多,因对老师三天来的课程内容深有感触,故借着整理学习心得的机会,将三天来的培训课程做了一个
- python内置函数大全
2002wmj
python
最近一直在看python的document,打算在基础方面重点看一下python的keyword、Build-in Function、Build-in Constants、Build-in Types、Build-in Exception这四个方面,其实在看的时候发现整个《The Python Standard Library》章节都是很不错的,其中描述了很多不错的主题。先把Build-in Fu
- JSP页面通过JQUERY合并行
357029540
JavaScriptjquery
在写程序的过程中我们难免会遇到在页面上合并单元行的情况,如图所示
如果对于会的同学可能很简单,但是对没有思路的同学来说还是比较麻烦的,提供一下用JQUERY实现的参考代码
function mergeCell(){
var trs = $("#table tr");
&nb
- Java基础
冰天百华
java基础
学习函数式编程
package base;
import java.text.DecimalFormat;
public class Main {
public static void main(String[] args) {
// Integer a = 4;
// Double aa = (double)a / 100000;
// Decimal
- unix时间戳相互转换
adminjun
转换unix时间戳
如何在不同编程语言中获取现在的Unix时间戳(Unix timestamp)? Java time JavaScript Math.round(new Date().getTime()/1000)
getTime()返回数值的单位是毫秒 Microsoft .NET / C# epoch = (DateTime.Now.ToUniversalTime().Ticks - 62135
- 作为一个合格程序员该做的事
aijuans
程序员
作为一个合格程序员每天该做的事 1、总结自己一天任务的完成情况 最好的方式是写工作日志,把自己今天完成了什么事情,遇见了什么问题都记录下来,日后翻看好处多多
2、考虑自己明天应该做的主要工作 把明天要做的事情列出来,并按照优先级排列,第二天应该把自己效率最高的时间分配给最重要的工作
3、考虑自己一天工作中失误的地方,并想出避免下一次再犯的方法 出错不要紧,最重
- 由html5视频播放引发的总结
ayaoxinchao
html5视频video
前言
项目中存在视频播放的功能,前期设计是以flash播放器播放视频的。但是现在由于需要兼容苹果的设备,必须采用html5的方式来播放视频。我就出于兴趣对html5播放视频做了简单的了解,不了解不知道,水真是很深。本文所记录的知识一些浅尝辄止的知识,说起来很惭愧。
视频结构
本该直接介绍html5的<video>的,但鉴于本人对视频
- 解决httpclient访问自签名https报javax.net.ssl.SSLHandshakeException: sun.security.validat
bewithme
httpclient
如果你构建了一个https协议的站点,而此站点的安全证书并不是合法的第三方证书颁发机构所签发,那么你用httpclient去访问此站点会报如下错误
javax.net.ssl.SSLHandshakeException: sun.security.validator.ValidatorException: PKIX path bu
- Jedis连接池的入门级使用
bijian1013
redisredis数据库jedis
Jedis连接池操作步骤如下:
a.获取Jedis实例需要从JedisPool中获取;
b.用完Jedis实例需要返还给JedisPool;
c.如果Jedis在使用过程中出错,则也需要还给JedisPool;
packag
- 变与不变
bingyingao
不变变亲情永恒
变与不变
周末骑车转到了五年前租住的小区,曾经最爱吃的西北面馆、江西水饺、手工拉面早已不在,
各种店铺都换了好几茬,这些是变的。
三年前还很流行的一款手机在今天看起来已经落后的不像样子。
三年前还运行的好好的一家公司,今天也已经不复存在。
一座座高楼拔地而起,
- 【Scala十】Scala核心四:集合框架之List
bit1129
scala
Spark的RDD作为一个分布式不可变的数据集合,它提供的转换操作,很多是借鉴于Scala的集合框架提供的一些函数,因此,有必要对Scala的集合进行详细的了解
1. 泛型集合都是协变的,对于List而言,如果B是A的子类,那么List[B]也是List[A]的子类,即可以把List[B]的实例赋值给List[A]变量
2. 给变量赋值(注意val关键字,a,b
- Nested Functions in C
bookjovi
cclosure
Nested Functions 又称closure,属于functional language中的概念,一直以为C中是不支持closure的,现在看来我错了,不过C标准中是不支持的,而GCC支持。
既然GCC支持了closure,那么 lexical scoping自然也支持了,同时在C中label也是可以在nested functions中自由跳转的
- Java-Collections Framework学习与总结-WeakHashMap
BrokenDreams
Collections
总结这个类之前,首先看一下Java引用的相关知识。Java的引用分为四种:强引用、软引用、弱引用和虚引用。
强引用:就是常见的代码中的引用,如Object o = new Object();存在强引用的对象不会被垃圾收集
- 读《研磨设计模式》-代码笔记-解释器模式-Interpret
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
package design.pattern;
/*
* 解释器(Interpreter)模式的意图是可以按照自己定义的组合规则集合来组合可执行对象
*
* 代码示例实现XML里面1.读取单个元素的值 2.读取单个属性的值
* 多
- After Effects操作&快捷键
cherishLC
After Effects
1、快捷键官方文档
中文版:https://helpx.adobe.com/cn/after-effects/using/keyboard-shortcuts-reference.html
英文版:https://helpx.adobe.com/after-effects/using/keyboard-shortcuts-reference.html
2、常用快捷键
- Maven 常用命令
crabdave
maven
Maven 常用命令
mvn archetype:generate
mvn install
mvn clean
mvn clean complie
mvn clean test
mvn clean install
mvn clean package
mvn test
mvn package
mvn site
mvn dependency:res
- shell bad substitution
daizj
shell脚本
#!/bin/sh
/data/script/common/run_cmd.exp 192.168.13.168 "impala-shell -islave4 -q 'insert OVERWRITE table imeis.${tableName} select ${selectFields}, ds, fnv_hash(concat(cast(ds as string), im
- Java SE 第二讲(原生数据类型 Primitive Data Type)
dcj3sjt126com
java
Java SE 第二讲:
1. Windows: notepad, editplus, ultraedit, gvim
Linux: vi, vim, gedit
2. Java 中的数据类型分为两大类:
1)原生数据类型 (Primitive Data Type)
2)引用类型(对象类型) (R
- CGridView中实现批量删除
dcj3sjt126com
PHPyii
1,CGridView中的columns添加
array(
'selectableRows' => 2,
'footer' => '<button type="button" onclick="GetCheckbox();" style=&
- Java中泛型的各种使用
dyy_gusi
java泛型
Java中的泛型的使用:1.普通的泛型使用
在使用类的时候后面的<>中的类型就是我们确定的类型。
public class MyClass1<T> {//此处定义的泛型是T
private T var;
public T getVar() {
return var;
}
public void setVa
- Web开发技术十年发展历程
gcq511120594
Web浏览器数据挖掘
回顾web开发技术这十年发展历程:
Ajax
03年的时候我上六年级,那时候网吧刚在小县城的角落萌生。传奇,大话西游第一代网游一时风靡。我抱着试一试的心态给了网吧老板两块钱想申请个号玩玩,然后接下来的一个小时我一直在,注,册,账,号。
彼时网吧用的512k的带宽,注册的时候,填了一堆信息,提交,页面跳转,嘣,”您填写的信息有误,请重填”。然后跳转回注册页面,以此循环。我现在时常想,如果当时a
- openSession()与getCurrentSession()区别:
hetongfei
javaDAOHibernate
来自 http://blog.csdn.net/dy511/article/details/6166134
1.getCurrentSession创建的session会和绑定到当前线程,而openSession不会。
2. getCurrentSession创建的线程会在事务回滚或事物提交后自动关闭,而openSession必须手动关闭。
这里getCurrentSession本地事务(本地
- 第一章 安装Nginx+Lua开发环境
jinnianshilongnian
nginxluaopenresty
首先我们选择使用OpenResty,其是由Nginx核心加很多第三方模块组成,其最大的亮点是默认集成了Lua开发环境,使得Nginx可以作为一个Web Server使用。借助于Nginx的事件驱动模型和非阻塞IO,可以实现高性能的Web应用程序。而且OpenResty提供了大量组件如Mysql、Redis、Memcached等等,使在Nginx上开发Web应用更方便更简单。目前在京东如实时价格、秒
- HSQLDB In-Process方式访问内存数据库
liyonghui160com
HSQLDB一大特色就是能够在内存中建立数据库,当然它也能将这些内存数据库保存到文件中以便实现真正的持久化。
先睹为快!
下面是一个In-Process方式访问内存数据库的代码示例:
下面代码需要引入hsqldb.jar包 (hsqldb-2.2.8)
import java.s
- Java线程的5个使用技巧
pda158
java数据结构
Java线程有哪些不太为人所知的技巧与用法? 萝卜白菜各有所爱。像我就喜欢Java。学无止境,这也是我喜欢它的一个原因。日常
工作中你所用到的工具,通常都有些你从来没有了解过的东西,比方说某个方法或者是一些有趣的用法。比如说线程。没错,就是线程。或者确切说是Thread这个类。当我们在构建高可扩展性系统的时候,通常会面临各种各样的并发编程的问题,不过我们现在所要讲的可能会略有不同。
- 开发资源大整合:编程语言篇——JavaScript(1)
shoothao
JavaScript
概述:本系列的资源整合来自于github中各个领域的大牛,来收藏你感兴趣的东西吧。
程序包管理器
管理javascript库并提供对这些库的快速使用与打包的服务。
Bower - 用于web的程序包管理。
component - 用于客户端的程序包管理,构建更好的web应用程序。
spm - 全新的静态的文件包管
- 避免使用终结函数
vahoa.ma
javajvmC++
终结函数(finalizer)通常是不可预测的,常常也是很危险的,一般情况下不是必要的。使用终结函数会导致不稳定的行为、更差的性能,以及带来移植性问题。不要把终结函数当做C++中的析构函数(destructors)的对应物。
我自己总结了一下这一条的综合性结论是这样的:
1)在涉及使用资源,使用完毕后要释放资源的情形下,首先要用一个显示的方
![f_n\left ( x \right )\rightrightarrows f\left ( x \right ),x\in \left [ a,b \right ]](http://img.e-com-net.com/image/info8/61cb9a03797f4322be2559e191f5790c.png) ,且每个
,且每个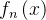 均在
均在![\left [ a,b \right ]](http://img.e-com-net.com/image/info8/e1e7696a40bd4d439adc8a6633698b38.png) 上可积
上可积 函数列
函数列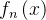 的极限函数
的极限函数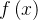 也在
也在![\left [ a,b \right ]](http://img.e-com-net.com/image/info8/e1e7696a40bd4d439adc8a6633698b38.png) 上可积;从而有这样的公式:
上可积;从而有这样的公式: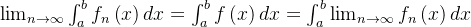 ;那我们会想,勒贝格积分与极限能否交换顺序?事实上这只能在很弱的条件下进行;
;那我们会想,勒贝格积分与极限能否交换顺序?事实上这只能在很弱的条件下进行;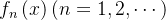 为可测集
为可测集 上的非负可测函数渐升序列
上的非负可测函数渐升序列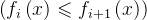 ,且
,且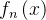 在
在 上几乎处处收敛于
上几乎处处收敛于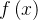 (即
(即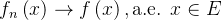 ),则有
),则有 ;
;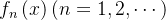 为可测集
为可测集 上的非负可测函数序列,则有:
上的非负可测函数序列,则有: ;其定理还有一个推论:已知
;其定理还有一个推论:已知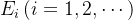 为
为 的互不相交可测子集列,且
的互不相交可测子集列,且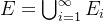 ,则:
,则: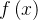 在
在 上有积分
上有积分
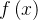 在每个
在每个 上均有积分,且有
上均有积分,且有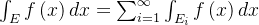 ;
;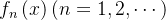 为可测集
为可测集 上的非负可测函数序列,则有:
上的非负可测函数序列,则有: ;这个引理可通过设中间非负可测函数列由列维定理证明得到,其中不等号可能成立的特例为:
;这个引理可通过设中间非负可测函数列由列维定理证明得到,其中不等号可能成立的特例为:![h_n\left ( x \right )=\left\{\begin{matrix} m, &x\in \left ( 0,\frac{1}{m} \right ) \\ 0, & x\in \left [ \frac{1}{m},1 \right ] \end{matrix}\right.](http://img.e-com-net.com/image/info8/f43290a260db4d15bcbb5761212f6ff0.png) ;
;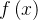 在
在![\left [ a,b \right ]](http://img.e-com-net.com/image/info8/e1e7696a40bd4d439adc8a6633698b38.png) 上勒贝格可积(可简写为
上勒贝格可积(可简写为![f\in L\left ( \left [ a,b \right ] \right )](http://img.e-com-net.com/image/info8/b727187002ec43368731fbf7880a2e3e.png) ),则:
),则: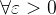 ,
,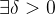 ,使得
,使得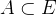 且
且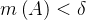 时,有
时,有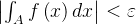 ;
;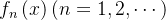 为可测集
为可测集 上的非负可测函数序列,其控制函数为
上的非负可测函数序列,其控制函数为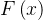 (即满足
(即满足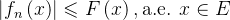 ),且
),且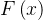 在
在 上勒贝格可积(可简写为
上勒贝格可积(可简写为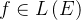 );则:
);则: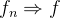 (即
(即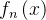 依测度收敛于
依测度收敛于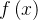 )
)
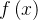 在
在 上是勒贝格可积的,且有
上是勒贝格可积的,且有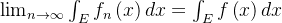 ;
;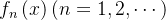 在可测集
在可测集 上勒贝格可积(即
上勒贝格可积(即 ),且满足这两个条件:
),且满足这两个条件: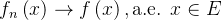 ;
; 一个勒贝格可积的
一个勒贝格可积的 在可测集
在可测集 上,使得
上,使得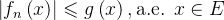 ,则
,则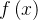 在
在 上是勒贝格可积的,且有
上是勒贝格可积的,且有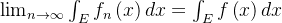 ;
;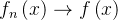 和
和 条件当然更好;条件更弱一些就是定理后面写着的
条件当然更好;条件更弱一些就是定理后面写着的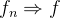 (依测度收敛)了;
(依测度收敛)了;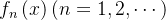 为有限测度
为有限测度 可测集
可测集 上的非负可测函数序列,且
上的非负可测函数序列,且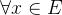 ,
,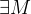 为常数,有
为常数,有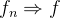 (即
(即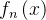 依测度收敛于
依测度收敛于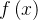 )和
)和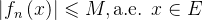 ;则
;则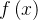 在
在 上是勒贝格可积的,且有
上是勒贝格可积的,且有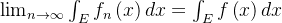 ;同样的,这个定理也可以像2里说的那样将条件稍稍加强,比如
;同样的,这个定理也可以像2里说的那样将条件稍稍加强,比如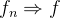 依测度收敛换成几乎处处收敛甚至逐点收敛(也就是收敛),
依测度收敛换成几乎处处收敛甚至逐点收敛(也就是收敛),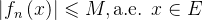 换成对于每个
换成对于每个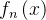 ,
, 均成立等等;
均成立等等;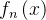 的情况下求
的情况下求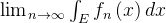 的值,解决方法通常是:首先我们需要确定
的值,解决方法通常是:首先我们需要确定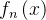 为有界可测函数列,有界性可以和之后找控制函数一起弄,而验证其为可测函数列只需要知道“可测集上的连续函数一定可测”即可验证;然后找出
为有界可测函数列,有界性可以和之后找控制函数一起弄,而验证其为可测函数列只需要知道“可测集上的连续函数一定可测”即可验证;然后找出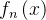 的控制函数
的控制函数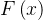 ,通常我们需要对含
,通常我们需要对含 的取值进行分类,比如求
的取值进行分类,比如求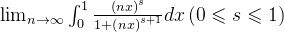 时,我们自然会想到对
时,我们自然会想到对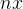 的取值进行分类(
的取值进行分类(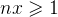 和
和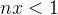 的情况)求其控制函数,一般得到的控制函数为按照分类整合的分段函数;由于得到的控制函数
的情况)求其控制函数,一般得到的控制函数为按照分类整合的分段函数;由于得到的控制函数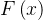 可以判断是黎曼可积的(连续必可积),黎曼可积必勒贝格可积(由此得到了勒贝格控制收敛定理的第一个大条件),然后通过求出
可以判断是黎曼可积的(连续必可积),黎曼可积必勒贝格可积(由此得到了勒贝格控制收敛定理的第一个大条件),然后通过求出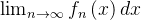 的值并设为
的值并设为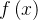 得到了
得到了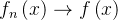 (由此得到了勒贝格控制收敛定理的第二个大条件);结合这两个大条件,由勒贝格控制收敛定理可得式子
(由此得到了勒贝格控制收敛定理的第二个大条件);结合这两个大条件,由勒贝格控制收敛定理可得式子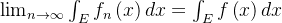 成立,由这个式子可以帮助我们解决要求
成立,由这个式子可以帮助我们解决要求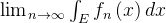 的值;
的值;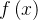 为
为![\left [ a,b \right ]](http://img.e-com-net.com/image/info8/e1e7696a40bd4d439adc8a6633698b38.png) 上的有界函数,则有:
上的有界函数,则有: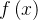 在
在![\left [ a,b \right ]](http://img.e-com-net.com/image/info8/e1e7696a40bd4d439adc8a6633698b38.png) 上黎曼可积
上黎曼可积
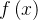 在
在![\left [ a,b \right ]](http://img.e-com-net.com/image/info8/e1e7696a40bd4d439adc8a6633698b38.png) 上的不连续点集是零测集;
上的不连续点集是零测集;