通信原理基础知识

通信原理基础知识

按照老师划的重点整理的，缺少一些内容，但是有很多个人理解，参考书是通信原理教程（樊昌信第四版），只有基础知识，后面打起来太麻烦了

第一章 概论

信息量：消息中包含的信息量是关于事件概率的函数。概率越小，信息量越大。”明天太阳升起“信息量就很小，而”世界明天毁灭“信息量就很大。

和信息熵计算公式相同：$I=-lo{g}_{a}P(x)$,$a$一般取2，单位是bit。

信息熵和信息量表达的含义是不同的，信息熵是信息的不确定程度，描述的是事件的不确定性。而信息量则是，已知信息包含内容发生了，带给了我们多少信息。

如果信息独立：$I=\sum I_i$，结合概率公式来考虑，很容易证明。

码元：就是数字信号中一个二进制编码。

码元速率：单位时间内传输的码元速率，单位是波特(Baud)

信息速率：单位时间内传输的信息量，单位是比特/秒(b/s)

信道模型：调制信道模型和编码信道模型

调制信道模型：$e_o(t)=f[e_i(t)]+n(t)$，其中$n(t)$永远存在，成为加性噪声。而当$f[e_i(t)]=k(t)e_i(t)$时i，$k(t)$称为乘性噪声，当$k(t)$为常数时（例如在同轴电缆等有线传输）称为恒参信道，$k(t)$不恒定时，称为随参信号。可以理解为模拟信号，因为函数一般表示的是连续信号。

编码信道模型：描述的是数字信号，Eg：二进制编码，P(1/0)表示0传输为1的概率。

第二章 信号

确定信号与随机信号

确定信号：取值在任何时间都是确定可预知的信号，分为周期信号和非周期信号

随机信号：取值不确定、无法预知的信号。如果信号有统计规律，把这种信号看作一个随机过程。（比如一个平均值为1、方差为1的噪声）

能量信号与功率信号

能量信号：$0<E={\int }_{\infty }^{\infty }{s}^2(t)dt<\infty$，能量为一有限正值。

功率信号：$0<P=li{m}_{T\to \infty }\frac{1}{T}{\int }_{T/2}^{-T/2}{s}^2(t)dt<\infty$，功率为一有限正值，能衡量无穷大。

确定信号的性质

频域性质

• 功率信号的频谱（P22）

  就是周期信号的傅里叶变换，也就是离散傅里叶级数，${\omega }_0$是数字角频率
  $$C(jn{\omega }_0)=\frac{1}{T}{\int }_{-T/2}^{T/2}s(t)e^{-jn{\omega }_{0}t}dt$$

• 能量信号的频谱密度（P23）

  就是傅里叶变换，频谱密度就是连续的频谱，纵坐标应该理解为单位频带内的频率分量大小，参考概率密度
  $$S(\omega )={\int }_{-\infty }^{\infty }s(t)e^{-j\omega t}dt$$

• 能量信号的能量谱密度（P26）

  $E={\int }_{\infty }^{\infty }{s}^2(t)dt={\int }_{\infty }^{\infty }|S(f){|}^{2}df$，Parseval定理

  $G(f)=|S(f){|}^2$就是能量谱密度，就是频率$f$附近的能量，或者说是单位频带内的能量

  ps：能量谱密度是偶函数，积分可以改写

• 功率信号的功率谱密度（P27）

  $P(f)=li{m}_{T\to \infty }\frac{1}{T}|S_T(f){|}^2$

  表示$f$附近的功率，$S_T$表示截取一段长度为T的信号$s_t$的频谱

时域性质

• 自相关函数

  能量信号：$R(\tau )={\int }_{-\infty }^{\infty }s(t)s(t+\tau )dt$

  功率信号：$R(\tau )=li{m}_{T\to \infty }\frac{1}{T}{\int }_{T/2}^{-T/2}s(t)s(t+\tau )dt$

  自相关反应一个信号与自身延迟$\tau$之间的关系，当$\tau =0$时，能量信号的自相关函数=信号的能量

• 互相关函数

  能量信号：$R_{12}(\tau )={\int }_{-\infty }^{\infty }{s}_1(t)s_2(t+\tau )dt$

  功率信号：$R_{12}(\tau )=li{m}_{T\to \infty }\frac{1}{T}{\int }_{T/2}^{-T/2}{s}_1(t)s_2(t+\tau )dt$

  互相关不满足交换律

随机信号的性质

常见分布

• 正态分布

  $P_X(x)=\frac{1}{\sqrt{(}2\pi )\sigma }exp[-\frac{(x-a{)}^2}{2{\sigma }^2}]$

• 均匀分布

  $P_X(x)=\frac{1}{b-a}a\le x\le b$,其余为0

• 瑞利分布

  $P_X(x)=\frac{2x}{a}exp(-\frac{x^2}{a})x\ge 0$

  两个独立相同的正态分布作为坐标的向量的模，比如多径失真的时候，就可能出现两个高斯分布的噪声正交组合的情况

• 莱斯分布（在后面）

数学特征

• 数学期望

  $E_x={\int }_{-\infty }^{\infty }x{p}_X(x)dx$

  就是信号平均值

• 方差（P32)

  $D(X)={\sigma }_X^2=E[(X-\overline{X}{)}^2]$

  我们曾经学的是样本方差，每个样本都是等权的，但在随机过程里是加权的，可以理解为采样了很多次，那样本个数应该和概率成正比

  连续：$D(x)={\int }_{-\infty }^{\infty }(x-\overline{X}{)}^2{p}_X(x)dx$

  离散的懒得打了

• 矩（P33）

  期望是一阶原点矩，方差是二阶中心矩，很简单的，不知道回去看概率论与数理统计

随机过程

基本概念（P33）

信号每个时间点都是一个随机变量，这些随机变量的集合就是随机过程（个人理解）

平均值和方差就是将$X$换成$X(t_i)$，$X(t_i)$就是$t_i$时刻的随机变量

随机变量自相关函数：$R_X(t_1,t_2)=E[X(t_1)X(t_2)]$，表示的是两个时刻对同意信号抽样的两个随机值的相关程度

自相关函数和功率谱密度

• 自相关函数的性质（P35）

  略

• 功率谱密度的性质（P36）

  • 实函数+偶函数

白噪声与带限白噪声

• 白噪声

  功率谱密度为常数$n_0/2$，双边白噪声，单边为$n_0$

• 带限白噪声

  带宽受限白噪声，功率谱密度为$-f_H$到$f_H$之间的矩形，值为$n_0/2$

高斯过程（P41）

一维概率密度函数：$P_X(x,t_1)=\frac{1}{\sqrt{(}2\pi )\sigma }exp[-\frac{(x-a{)}^2}{2{\sigma }^2}]$

每个时刻的随机变量都是高斯分布，高斯过程的随机变量之间互不相关且相互独立。

窄带随机过程

就是带宽受限的随机过程

正弦波+窄带高斯过程

一般来说传输的信号都是经过正弦波调制的（调制在后面），可以近似为正弦波（余弦波），在信号传播过程中，相位发生失真（随机过程），并且叠加一个随机噪声（窄带高斯过程）

信号可以表示为$r(t)=Acos({\omega }_{0}t+\theta )+n(t)$

莱斯分布就是信号包络的概率密度函数，公式比较复杂，见书。当A=0时，包络为瑞利分布，高斯随机过程的包络为瑞利分布。

PS：这很关键，为啥是包络的概率密度函数。必须提前提及一下调制是什么，因为我们本来的信号频率很低，但是我们将它乘上正弦信号，做了频谱搬迁，所以包络才是我们原本的信号

线性系统/冲激响应/传输函数

我不想细说了，希望你信号与系统学好了。

输出随机过程的概率分布

高斯随机过程通过线性系统后仍为高斯随机过程，但是数字特征改变。

证明方法是，将卷积写成求和+极限形式，求和每个部分都是一个随机变量的高斯分布，根据概率论知识，和也为随即正态分布。

第三章 模拟调制系统

模拟调制的类型

线性调制和非线性调制。

线性调制：频谱搬移

非线性调制：频谱搬移+新的频率分量

线性调制（幅度调制AM）

载波：$c(t)=Acos{\omega }_{o}t$

调制信号：$m(t)$

载波与调制信号相乘：$s^{\prime }(t)=m(t)Acos{\omega }_{0}t$

$S^{\prime }(t)$就是$M(t)$的频谱搬迁，我们可以直接把$s^{\prime }(t)$发送出去，但是它其实包含了很多冗余信息，我们也可以部分发射，就有了很多调制方法

振幅调制AM

如果信号可以分成直流信号+交流信号$m(t)=1+m^{\prime }(t)$，其中$|m^{\prime }(t)|\le 1$，则$s^{\prime }(t)=[1+m^{\prime }(t)]Acos{\omega }_{0}t$，把它直接发送出去，因为发送的内容包含了载波，直接整流+低通滤波器就可以搞定。但是由于需要发送直流信号，所以功率比较大（P56）

PS：双边带就是直接发送，但是需要对方知道载波，在对面乘载波后再解调，缺点是需要乘对方知道载波，且带宽太大。单边带用的比双边带多，因为频谱有正负，是对称的，实际上知道一半就够了，但是对面解调麻烦一点。残留边带是部分载波+单边带多一点，我不是太确定原理。

非线性调制（P60）

基本原理

设载波信号$c(t)=Acos({\omega }_{0}t+{\varphi }_0)$，瞬时相位$\varphi (t)={\omega }_{0}t+{\varphi }_0$，瞬时频率为${\omega }_0$

当${\omega }_0$不是常量时，我们定义${\omega }_i(t)=\frac{d\varphi (t)}{dt}$，是时间的常数

则$\varphi (t)=\int {\omega }_i(t)dt+{\varphi }_0$

如果$\varphi (t)$随调制信号$m(t)$改变，则称为角度调制。

**相位调制：**若随$m(t)$线性变化，$\varphi (t)={\omega }_{0}t+{\varphi }_0+k_{p}m(t)$，则称为相位调制

**频率调制：**若瞬时频率随调制信号线性变化，${\omega }_i(t)={\omega }_0+k_{f}m(t)$，称为频率调制

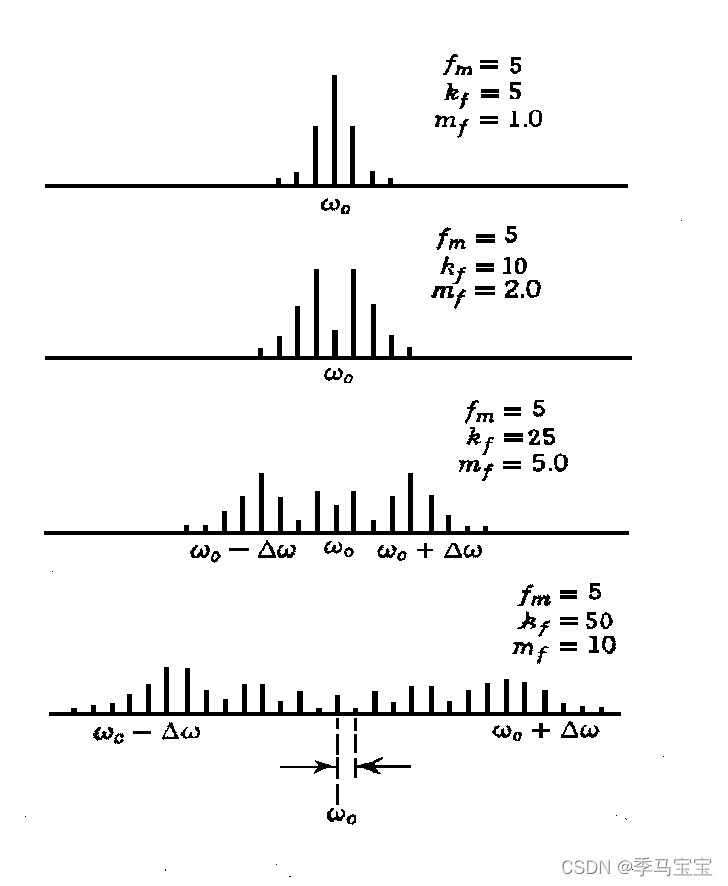
已调信号的频谱特征（P62）

• 边频成对

• 大部分功率集中在有限带宽内

• 当调制指数$m_f<<1$ 时，带宽B基本等于$2{\omega }_m$，称为窄带调频。

• 当$m_f>1$ 时，
  带宽B：
  $$\begin{gathered} B\approx 2(\Delta \omega +{\omega }_m) \\ \approx 2(\Delta f+f_m) \end{gathered}$$

  式中，
  $\Delta f$ － 调制频移，
  $f_m$ － 调制信号频率

  ​ 上面是rad/s

  ​ 下面是Hz