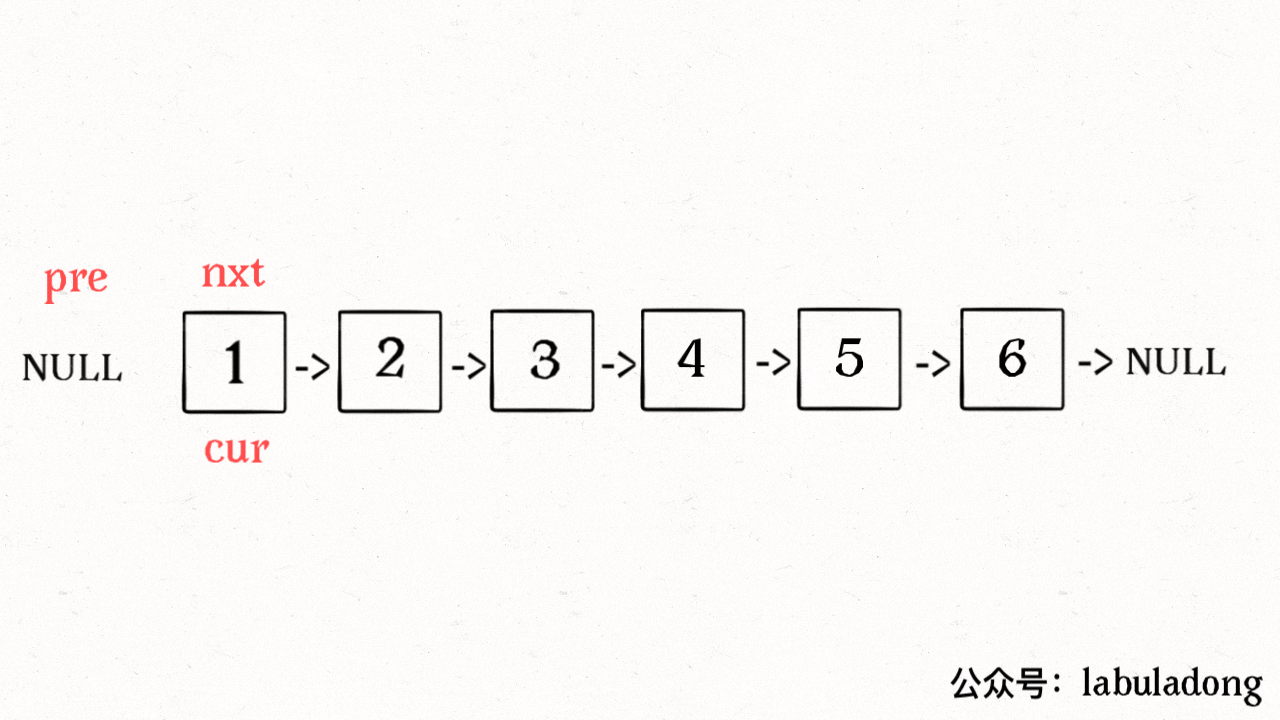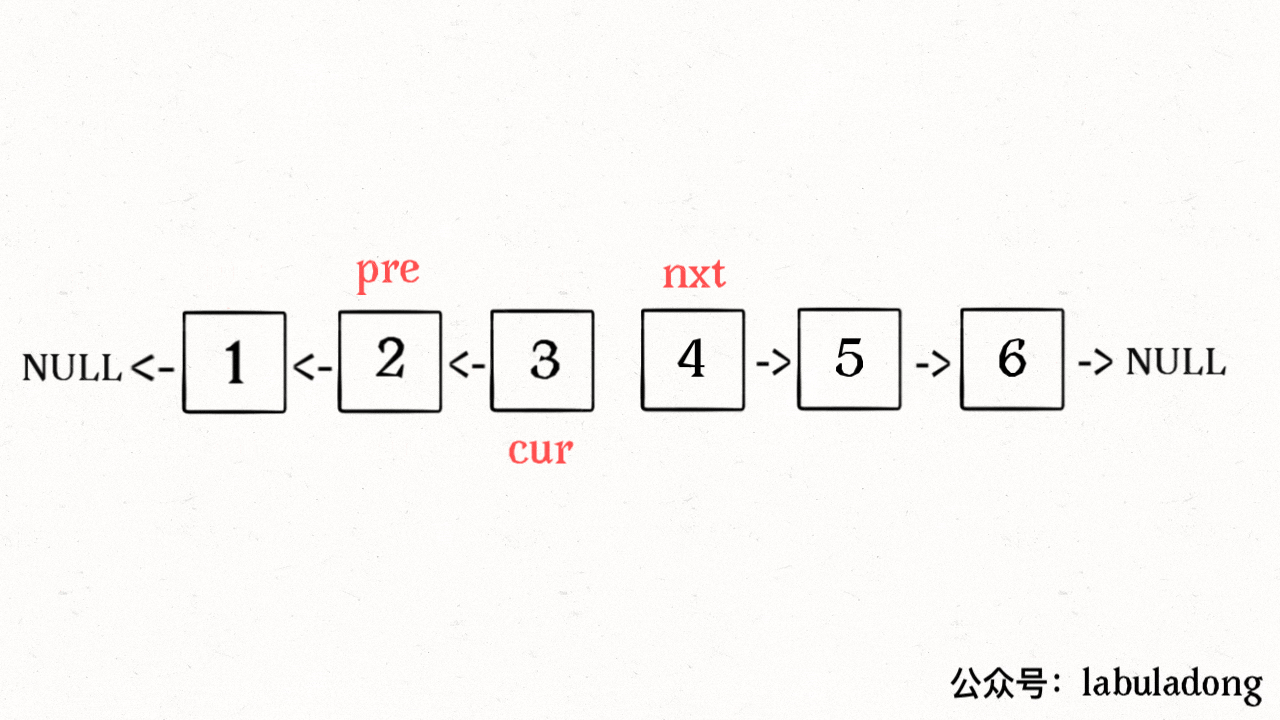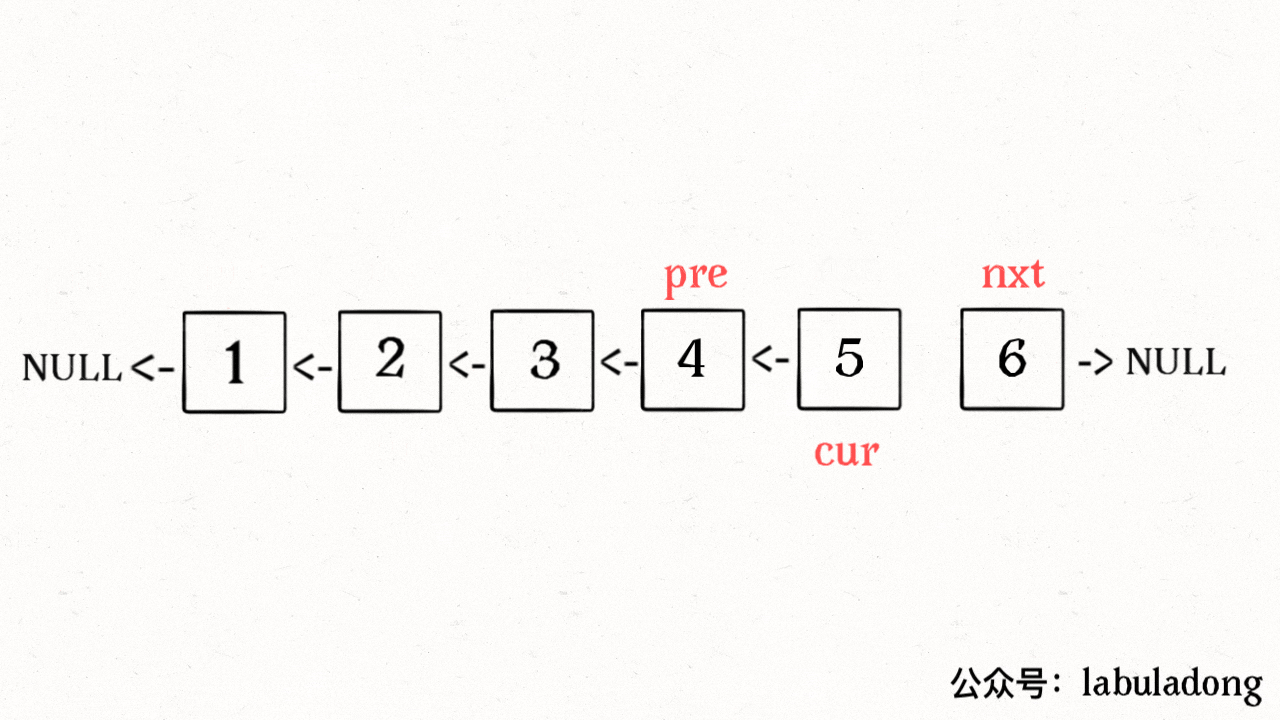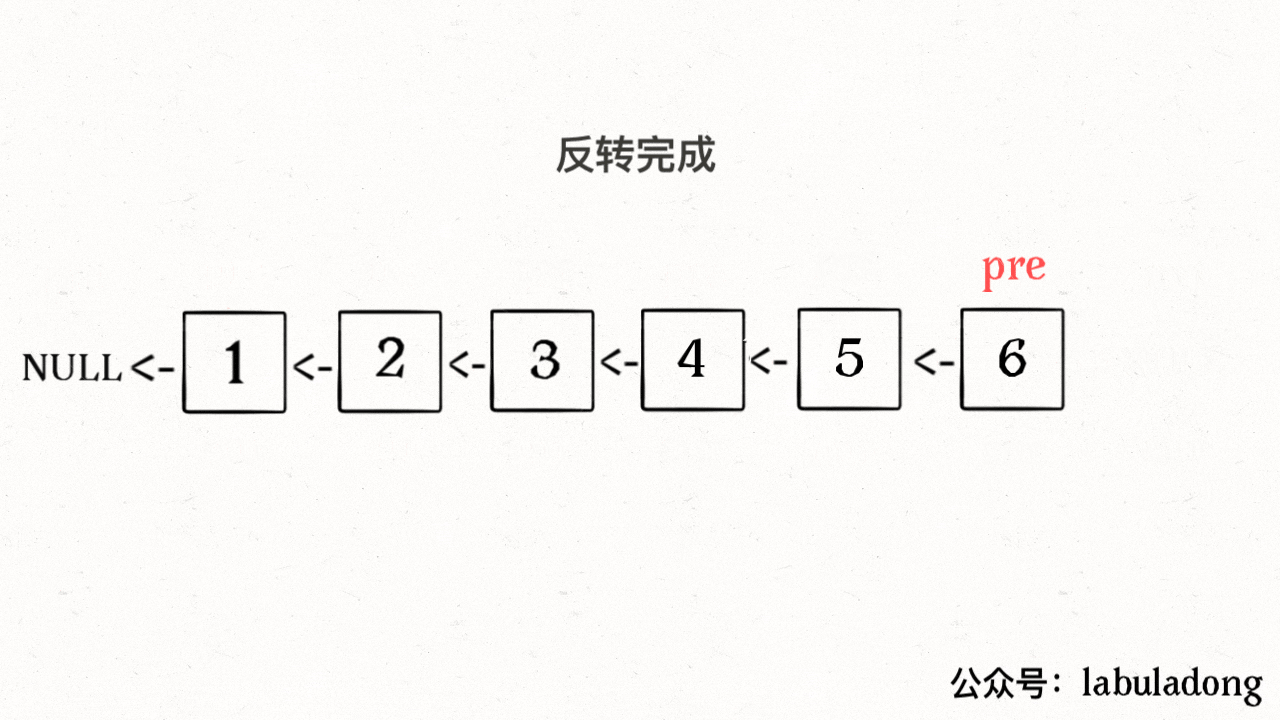算法刷题笔记 Day_3 链表题目再刷，多道链表递归和迭代

目录

一、链表

1. 反转单链表 ——递归

2. 反转单链表 ——迭代

3. 如何判断回文链表

---

一、链表

1. 反转单链表 ——递归

① 力扣第 206 题「 反转链表」——Easy：

迭代解法：

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode prev = null;
        ListNode curr = head;
        while (curr != null) {
            ListNode next = curr.next;
            curr.next = prev; //这两行代码是用 头插法，最后prev是生成的反转链表！
            prev = curr;
            curr = next;
        }
        return prev;
    }
}

复杂度分析

    时间复杂度：O(n)，其中 n 是链表的长度。需要遍历链表一次。

    空间复杂度：O(1)。

递归解法：

参考资料：递归魔法：反转单链表 :: labuladong的算法小抄

class Solution {
    public ListNode reverseList(ListNode head) {
        if(head==null||head.next==null)
            return head;
        ListNode last = reverseList(head.next);//这个是头节点 用来接收反转列表的头节点
        head.next.next = head;//形成双向链表！
        head.next = null;//切断双向链表 只保留一边 类似于尾巴
        return last;//返回反转链表
    }
}

解法思路：先走到最后一个结点，先实现双链表，然后变成单链表。

复杂度分析

    时间复杂度：O(n)，其中 n 是链表的长度。需要对链表的每个节点进行反转操作。

    空间复杂度：O(n),  其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间，最多为 n 层。

② 力扣第 92 题「 反转链表 II」——Medium：

这题递归解法，蛮烧脑的~

class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        if(left==1)
            return reverseN(head,right);
        head.next = reverseBetween(head.next,left-1,right-1);
        return head;
    }

    ListNode success = null;
    
    ListNode reverseN(ListNode head,int n){
        if (n==1){
            success = head.next; //这个success指向的是反转链表结尾的下一个结点！
            return head;
        }
        ListNode last = reverseN(head.next,n-1);
        head.next.next = head;
        head.next = success;// 让反转之后的 head 节点和后面的节点连起来
        return last;
    }
}

尽管每次执行head.next = success 都会让让节点指向了 success， 但是在下一层的 「归」中，head.next (也就是上一层中的 head) 的next 又把指向的success改成指向了head，这里就改过来了。这样到最外层的归时，只剩头节点的next还指向 success了

参考资料：递归魔法：反转单链表 :: labuladong的算法小抄

递归操作链表并不高效。和迭代解法相比，虽然时间复杂度都是 O(N)，但是迭代解法的空间复杂度是 O(1)，而递归解法需要堆栈，空间复杂度是 O(N)。所以考虑效率的话还是使用迭代算法更好。

2. 反转单链表 ——迭代

力扣第 25 题「 K 个一组翻转链表」——Hard：

这个题据说在面试中经常看到，且是Hard，下面看解决办法。

class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        if (head == null) return null;
        //区间[a,b)包含k个待反转的元素
        ListNode a = head, b = head;
        for (int i = 0; i < k; i++) {
            //如果下面区间不够k个，则不需要反转
            if (b == null) return head;
            b = b.next;
        }
        //反转begin到end的元素
        ListNode newHead = reverse(a, b);
        // 递归反转后续链表并连接起来
        a.next = reverseKGroup(b, k);
        return newHead;
    }

    // 反转以 begin 为头结点的链表
    // 反转区间 [begin, end) 的元素，注意是左闭右开
    ListNode reverse(ListNode begin, ListNode end) {
        ListNode pre, cur, next;
        pre = null;//最后的新链表头
        cur = begin;//目前链表
        while (cur != end) {
            next = cur.next; //表示cur当前结点的后续链表
            cur.next = pre;
            pre = cur;//头插法 pre永远是链表的头 可以理解为栈的栈顶，一直会是栈顶
            cur = next;//当前链表变为 抛出了前一个结点 剩下的链表段了
        }
        return pre;
    }
}

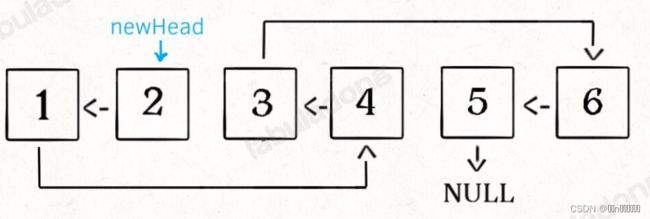
下面这个图是 函数reverse的解释图（反转链表的迭代方法）：

反转后的链表：

不得不说，这道题，结合递归和迭代，反转小链表是用的迭代，这样可以省空间，但是在主函数的递归reverseKGroup，仍需要O(n) 的空间复杂度的。这题是道Hard，不过明白道理之后也不是那么困难的了。

上面这几篇习题，对递归的使用尤为神奇，后续还得多复习复习才是！

3. 如何判断回文链表

力扣第 234 题「 回文链表」——Easy：

class Solution {
    public boolean isPalindrome(ListNode head) {

        //双指针前进
        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }//通过这步循环  可以把快慢指针——slow到中间位置，fast到末尾
        //下面这步操作也是十分必要，很精髓的一步
        if (fast != null) {//这步是帮助处理慢指针的位置（奇数链表），帮助奇数链表的slow变为中间位置再往后一位!
            slow = slow.next;
        }
        //接下来的步骤就是处理 slow之后的链表，将其反转！
        ListNode last = reverse(slow);
        ListNode front = head;
        //反转之后 开始将head和last判断，相当是 从链表“头”和“尾”开始向中间逼近 判断！
        while (last != null) {
            if (front.val != last.val)
                return false;
            front = front.next;
            last = last.next;
        }
        return true;
    }

    //反转链表的迭代方法
    ListNode reverse(ListNode head) {
        ListNode pre = null, cur = head;
        while (cur != null) {
            ListNode next = cur.next;
            cur.next = pre;
            pre = cur;
            cur = next;
        }
        return pre;//上面是头插法 迭代！空间复杂度为O(1),时间复杂度为O(n)
    }
    //TODO 这里reverse也可以是递归的方法，但是递归的方法空间复杂度是O(n),不划算！
}

解法思路：使用快慢指针，通过slow指针的位置，开始反转slow结点之后的链表形成last为头的链表，然后让head和last同时向中间逼近！

提示：别看代码多，其实思路很关键，先懂思路，才能走更远！

参考资料：如何判断回文链表 :: labuladong的算法小抄