算法刷题笔记 Day_4 再刷数组经典题目列表①

目录

一、数组

1. 一维数组中的前缀和

2. 二维矩阵中的前缀和

3. 差分数组

---

一、数组

首先衔接上文的7道数组题：算法刷题笔记 Day_2 7道数组题_Đến❦หัวใจ的博客-CSDN博客

下面我们继续刷，有关数据的题目。

1. 一维数组中的前缀和

① 力扣第 303 题「 区域和检索 - 数组不可变」——Easy：

让你计算数组区间内元素的和，这是一道标准的前缀和问题。

普通解法：

class NumArray {

    private int[] nums;

    public NumArray(int[] nums) {
        this.nums = nums;
    }
    
    public int sumRange(int left, int right) {
        int res = 0;
        for (int i = left; i <= right; i++) {
            res += nums[i];
        }
        return res;
    }
}

时间复杂度：O(n)。  //由于sumRange被一直调用，且该函数里有一个for循环。

空间复杂度：O(n)。  

前缀和问题解法：

class NumArray {
    //前缀和数组
    private int[] preSum;

    public NumArray(int[] nums) {
        // preSum[0] = 0，便于计算累加和
        preSum = new int[nums.length + 1];
        // 计算 nums 的累加和
        for (int i = 1; i < preSum.length; i++) {
            preSum[i] = nums[i-1] + preSum[i-1];
        }
    }
    
    public int sumRange(int left, int right) {
        return preSum[right+1]-preSum[left];
    }
}

解法思路：通过preSum数组，来记录每个前缀和的结果，需要注意的是，这个数组preSum需要比num[ ]大一个位置，因为preSum需要一个最初始的值，即preSum[0] = 0;，之后的数组便是存入每个num[i]的前缀和了~。

时间复杂度：O(1)。  //生成前缀和preSum[ ],这步操作是O(n)时间复杂度，但是外面现在计算的是sumRange函数的时间复杂度，经过前缀和操作后，sumRange函数仅仅需要做一次减法运算，避免了每次进行 for 循环调用，最坏时间复杂度为O(1)。

空间复杂度：O(n) 。

2. 二维矩阵中的前缀和

① 力扣第 304 题「 二维区域和检索 - 矩阵不可变」——Medium：

该题是计算二维矩阵中子矩阵的元素之和，如果采用常规解法，在区间直接for循环遍历出来的话，时间复杂度仍然很高，参考上面一题，所以这一题的做法同上边一致，采用前缀和，减少时间复杂度，进而优化代码。

class NumMatrix {

    private int[][] preSum;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;//m表示宽 n表示长
        System.out.println(m);
        if (m == 0 || n == 0) return;
        preSum = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                preSum[i][j] = preSum[i - 1][j] +  preSum[i][j - 1]
                        - preSum[i - 1][j - 1] + matrix[i - 1][j - 1] ;//计算每个矩阵的和
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return preSum[row2+1][col2+1] - preSum[row2+1][col1] - preSum[row1][col2+1] + preSum[row1][col1];
    }
}

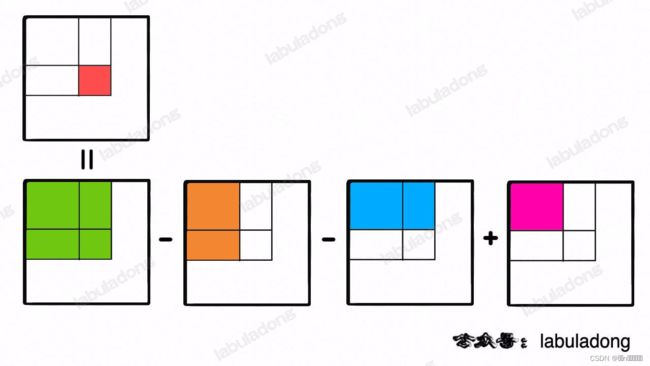
解题思路：做这道题更好的思路和一维数组中的前缀和是非常类似的，我们可以维护一个二维 preSum 数组，专门记录以原点为顶点的矩阵的元素之和，就可以用几次加减运算算出任何一个子矩阵的元素和。

sumRegion 函数中四个矩阵的减法如下图：

 sumRegion 函数的时间复杂度也用前缀和技巧优化到了 O(1)，这是典型的「空间换时间」思路。

前缀和主要适用的场景是原始数组不会被修改的情况下，频繁查询某个区间的累加和。

3. 差分数组

差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。

① 力扣第 370 题「 区间加法」——Medium （这题是会员题，我们看下面的图就好）

这个解法具体看该链接：小而美的算法技巧：差分数组 :: labuladong的算法小抄

解题思路：差分数组求解！

② 力扣第 1109 题「 航班预订统计」——Medium：

class Solution {
    public int[] corpFlightBookings(int[][] bookings, int n) {

        int[] nums = new int[n];
        Difference df = new Difference(nums);//初始化的数组！
        for (int[] booking : bookings) {
            int i = booking[0] - 1;
            int j = booking[1] - 1;
            int val = booking[2];
            //对区间nums[i..j]增加值val
            df.increment(i,j,val);
        }
        return df.result();

    }

    // 差分数组工具类
    class Difference {
        // 差分数组
        private int[] diff;

        /* 输入一个初始数组，区间操作将在这个数组上进行 */
        public Difference(int[] nums) {
            assert nums.length > 0;//在执行这个语句时假定该表达式为true；如果表达式计算为false，那么系统会报告一个AssertionError。
            diff = new int[nums.length];
            // 根据初始数组构造差分数组
            diff[0] = nums[0];
            for (int i = 1; i < nums.length; i++) {
                diff[i] = nums[i] - nums[i - 1];
            }
        }

        /* 给闭区间 [i, j] 增加 val（可以是负数）*/
        public void increment(int i, int j, int val) { //时间复杂度为O(1)!
            diff[i] += val;
            if (j + 1 < diff.length) {
                diff[j + 1] -= val;
            }
        }

        /* 返回结果数组 */
        public int[] result() {
            int[] res = new int[diff.length];
            // 根据差分数组构造结果数组
            res[0] = diff[0];
            for (int i = 1; i < diff.length; i++) {
                res[i] = res[i - 1] + diff[i];
            }
            return res;
        }
    }

}

解题思路：该题目本质上来说，就是一个差分数组的题目，通过差分数组快速帮我们解决问题，下面使用到的差分数组工具类就是很通用的一个东西了，我们只需要获取差分区间 [ i , j ]，然后再获取val值，通过工具类的差分方法，保存到diff[ ]数组中，最后再调用result()的方法返回差分数组的信息即可。

提示：如果不会差分数组了，自己画个图试试吧，自己手动记录一边就会很清楚啦。

时间复杂度：O(n)。 

空间复杂度：O(n) 。

③ 力扣第 1094 题「 拼车」——Medium：

class Solution {
    public boolean carPooling(int[][] trips, int capacity) {
    int[] nums = new int[1001];
    Difference df = new Difference(nums);
        for (int[] trip : trips) {
            int val = trip[0];
            int i = trip[1];
            int j = trip[2] - 1;
            df.increment(i,j,val);
        }

        int[] res = df.result();
        for (int i = 0; i < res.length; i++) {
            if (capacity < res[i])
                return false;
        }
        return true;
    }

    // 差分数组工具类
    class Difference {
        // 差分数组
        private int[] diff;

        /* 输入一个初始数组，区间操作将在这个数组上进行 */
        public Difference(int[] nums) {
            assert nums.length > 0;//在执行这个语句时假定该表达式为true；如果表达式计算为false，那么系统会报告一个AssertionError。
            diff = new int[nums.length];
            // 根据初始数组构造差分数组
            diff[0] = nums[0];
            for (int i = 1; i < nums.length; i++) {
                diff[i] = nums[i] - nums[i - 1];
            }
        }

        /* 给闭区间 [i, j] 增加 val（可以是负数）*/
        public void increment(int i, int j, int val) { //时间复杂度为O(1)!
            diff[i] += val;
            if (j + 1 < diff.length) {
                diff[j + 1] -= val;
            }
        }

        /* 返回结果数组 */
        public int[] result() {
            int[] res = new int[diff.length];
            // 根据差分数组构造结果数组
            res[0] = diff[0];
            for (int i = 1; i < diff.length; i++) {
                res[i] = res[i - 1] + diff[i];
            }
            return res;
        }
    }
}

解题思路：还是采用差分数组的模板，然后判断最后生成的res[ ]数组，看里面的各个值是否大于我们规定的capacity值，然后返回true || false。

时间复杂度：O(n)。 

空间复杂度：O(n) 。

注意：由于在题目中我们看到限制条件如下：

• 1 <= trips.length <= 1000
• trips[i].length == 3
• 1 <= numPassengersi <= 100
• 0 <= fromi < toi <= 1000
• 1 <= capacity <= 105

我们初始化数组为1000，数组初始到我们够用就可以啦~

int[] nums = new int[1000]; ///初始化数组长度

执行耗时:3 ms,击败了42.99% 的Java用户
内存消耗:41.1 MB,击败了53.14% 的Java用户