强化学习基础
强化学习基础
-
- 强化学习的几个基本要素
- 贝尔曼方程
- 序列决策问题
-
- ① 动态规划法(DP):
- ② 蒙特卡罗法(MC):
- ③ 时间差分法(TD)
强化学习的几个基本要素
1) s t s_t st: t t t 时刻环境的状态
2) a t a_t at: t t t 时刻智能体采取的动作
3) R t + 1 R_{t + 1} Rt+1: t t t 时刻智能体在状态 s t s_t st 下采取动作 a t a_t at 后,在 t + 1 t + 1 t+1 时刻得到的奖励。
4) π ( a ∣ s ) \pi(a|s) π(a∣s) : 智能体的策略 ,表示在状态 s s s 下采取动作 a a a 的概率。
π ( a ∣ s ) = P ( a t = a ∣ s t = s ) \pi(a|s) = P(a_t = a|s_t = s) π(a∣s)=P(at=a∣st=s)
5) P s s ′ a P_{ss^{\prime}} ^a Pss′a :环境的状态转化模型。表示在状态 s s s 下采取动作 a a a ,转到下一个状态 s ′ s^\prime s′的概率。
6) γ \gamma γ : 奖励衰减因子。 γ ∈ [ 0 , 1 ] \gamma \in [0, 1] γ∈[0,1],取 0 时表示完全贪婪策略,只关注当前步骤所获得的奖励值。
7) α \alpha α : 学习率。
8) ϵ \epsilon ϵ : 探索率,探索其他动作的概率。
9) V π ( s ) V_{\pi}(s) Vπ(s) : 智能体在状态 s s s 时通过策略 π \pi π 采取动作后的状态价值函数。
V π ( s ) = E π ( R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . ∣ s t = s ) V_{\pi}(s) = E_{\pi}(R_{t + 1} + \gamma R_{t + 2} + \gamma^2 R_{t + 3} + ... |s_t = s) Vπ(s)=Eπ(Rt+1+γRt+2+γ2Rt+3+...∣st=s)
10) Q π ( s , a ) Q_{\pi}(s, a) Qπ(s,a) : 智能体在状态 s s s 时通过策略 π \pi π 采取动作 a a a 后的动作价值函数。
Q π ( s , a ) = E π ( G t ∣ s t = s , a t = a ) = E π ( R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . ∣ s t = s , a t = a ) Q_{\pi}(s, a) = E_{\pi}(G_t | s_t = s, a_t = a) = E_{\pi}(R_{t + 1} + \gamma R_{t + 2} + \gamma^2 R_{t + 3} + ... |s_t = s, a_t = a) Qπ(s,a)=Eπ(Gt∣st=s,at=a)=Eπ(Rt+1+γRt+2+γ2Rt+3+...∣st=s,at=a)
从这里我们能看出来 γ γ γ 奖励衰减因子对Q函数的影响,γ越接近于1代表它越有远见会着重考虑后续状态的的价值,当γ接近0的时候就会变得近视只考虑当前的利益的影响。所以从0到1,算法就会越来越会考虑后续回报的影响。
贝尔曼方程
1)在 t t t 时刻的状态 s t s_t st 和 t + 1 t + 1 t+1 时刻的状态 s t + 1 s_{t + 1} st+1 满足递推关系:
V π ( s ) = E π ( R t + 1 + γ V π ( s t + 1 ) ∣ s t = s ) V_{\pi}(s) = E_{\pi}(R_{t + 1} + \gamma V_{\pi}(s_{t + 1}) |s_t = s) Vπ(s)=Eπ(Rt+1+γVπ(st+1)∣st=s)
即一个状态的价值由该状态所得的奖励以及后续下一个状态的价值按一定的衰减比例联合组成。
2)同理可得动作价值函数 Q π ( s , a ) Q_{\pi}(s, a) Qπ(s,a)的贝尔曼方程:
Q π ( s , a ) = E π ( R t + 1 + γ Q π ( s t + 1 , a t + 1 ) ∣ s t = s , a t = a ) Q_{\pi}(s, a) = E_{\pi}(R_{t + 1} + \gamma Q_{\pi}(s_{t + 1}, a_{t + 1}) |s_t = s, a_t = a) Qπ(s,a)=Eπ(Rt+1+γQπ(st+1,at+1)∣st=s,at=a)
Bellman方程实际上就是状态价值函数与动作价值函数的转换关系:
① V π ( s ) = ∑ a ∈ A π ( a ∣ s ) Q π ( s , a ) V_{\pi}(s) = \sum_{a \in A}\pi(a|s)Q_{\pi}(s, a) Vπ(s)=∑a∈Aπ(a∣s)Qπ(s,a)
状态价值 = = = ∑ \sum ∑ 该状态下所有的动作价值 × × × 该动作出现的概率
也就是说,状态价值函数是该状态下所有动作价值函数基于策略 π \pi π 的期望
② Q π ( s , a ) = R s + γ ∑ s ∈ S P s s ′ a V π ( s ′ ) Q_{\pi}(s, a) = R_s + \gamma\sum_{s \in S}P_{ss^{\prime}} ^aV_\pi(s^{\prime}) Qπ(s,a)=Rs+γ∑s∈SPss′aVπ(s′)
状态价值函数 = = = 即时奖励 + 奖励衰减因子 × × × 所有可能出现的下一状态的概率 × × × 该下一状态的状态价值
序列决策问题
时间差分方法(Temporal-Difference,简称TD) 和 蒙特卡洛方法是 无模型强化学习方法,动态规划方法是基于模型的强化学习方法。
时间差分方法与动态规划方法(DP) 和蒙特卡洛方法(MC) 相比,不同在于值函数的估计。

① 动态规划法(DP):
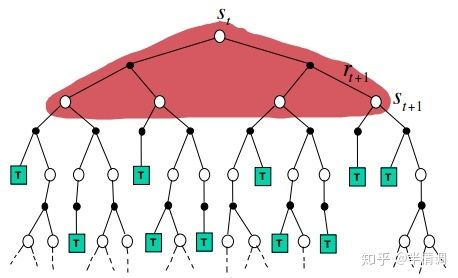
由于DP算法是基于模型的方法,所以当前状态 s s s 的所有后继状态 s ′ s^{\prime} s′ 是已知的,可以直接用后继状态的值函数估计当前值函数,也就是使用bellman方程求解值函数。
值函数估计公式: V ( s ) ← E π [ R t + 1 + γ V ( S t + 1 ) ] = ∑ a p ( s ′ , r ∣ s t , a ) [ r + γ V ( s ′ ) ] V(s)←E_\pi[R_{t+1}+\gamma V(S_{t + 1})] = \sum_ap(s^{\prime}, r | s_t, a)[r + \gamma V(s^{\prime})] V(s)←Eπ[Rt+1+γV(St+1)]=∑ap(s′,r∣st,a)[r+γV(s′)]
此处有一个概念:值函数的计算用到了 bootstapping 的方法。所谓 bootstrpping 本意是指自举,此处是指当前值函数的计算用到了后继状态的值函数。即用后继状态的值函数计算当前值函数。
② 蒙特卡罗法(MC):

在 Policy Gradient 中使用到了这种方法,MC可以应用在 model-free 的算法中,由于没有模型,后继状态无法全部得到,所以MC方法需要执行一个完整的 episode 才可以进行估计,需要回合结束才能更新。相对于动态规划方法,学习速度慢,效率低。
注意此处的 G t G_t Gt 是利用经验平均估计状态的值函数所计算出来的,表示一次完整的 episode 采样得到的奖励值折扣累加和。
值函数估计公式: V ( s ) ← V ( s ) + α ( G t − V ( s ) ) V(s)←V(s)+\alpha (G_t-V(s)) V(s)←V(s)+α(Gt−V(s))
G t ( n ) = R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . . . . γ n − 1 R t + n + γ n V ( S t + n ) G_t^{(n)} =R_{t+1}+γR_{t+2} +γ^2 R_{t+3} +......γ^{n−1} R_{t+n} +γ^n V(S_{t+n}) Gt(n)=Rt+1+γRt+2+γ2Rt+3+......γn−1Rt+n+γnV(St+n)
其中, G t G_t Gt 是一次完整的 episode 采样中从 t 时刻开始的总折扣奖励。
结合以上两个方法的优势就得到了TD算法,TD算法可以进行单步更新。
③ 时间差分法(TD)

时间差分方法结合了蒙特卡罗的 采样方法 和动态规划方法的 bootstrapping (利用后继状态的值函数估计当前值函数),使得TD可以适用于model-free的算法并且是单步更新,速度更快。
值函数计算方式如下:
V ( s ) ← V ( s ) + α ( R t + 1 + γ V ( s ′ ) − V ( s ) ) V(s)←V(s)+\alpha (R_{t+1}+\gamma V(s^′ )−V(s)) V(s)←V(s)+α(Rt+1+γV(s′)−V(s))
其中, R t + 1 + γ V ( s ′ ) R_{t+1}+\gamma V(s^′ ) Rt+1+γV(s′) 被称为TD目标, δ t = R t + 1 + γ V ( s ′ ) − V ( s ) \delta_t=R_{t+1}+\gamma V(s^′ )−V(s) δt=Rt+1+γV(s′)−V(s) 称为TD偏差。
可以发现其实就是把蒙特卡罗法中估计的 G t G_t Gt 替换成了TD目标,因为TD目标使用了 bootstrapping方法估计当前值函数,所以这样就结合了动态规划的优点避免了回合更新太慢的缺点。
时间差分方法包括 on-policy 的 Sarsa 方法和 off-policy 的 Q-Learning 方法。
TD(λ)可以通过在TD-target再根据bellman方程展开,就可扩展成n-step的形式,将每步求和取平均然后分别计算,并且赋予系数(系数加和为1)。
④ 三种方法异同点
蒙特卡洛方法:利用所有回报的累积估计值函数(这也是值函数最原始的定义)。蒙特卡罗的方法是随机采样,方差更大。
无偏估计;容易收敛;可以使用函数拟合;初值不敏感;理解简单容易使用。
动态规划和时间差分:用一步预测方法计算当前状态值函数。
时间差分方法的估计值有误差;通常情况比MC更有效; T D ( 0 ) TD(0) TD(0)收敛于 V π ( s ) V_\pi(s) Vπ(s);初值敏感。
不同:1.动态规划方法利用模型得到后继状态;2.时间差分方法利用实验采样得到后继状态。
⑤ 计算实例

