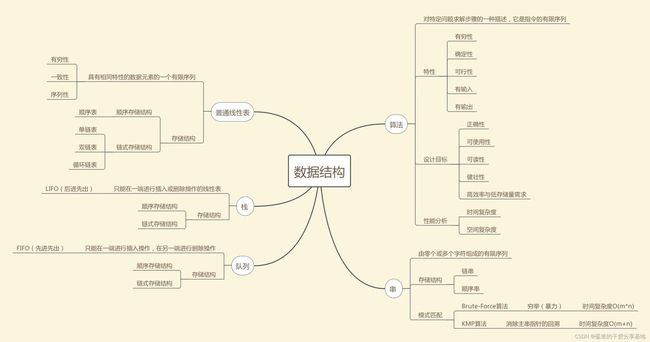
【数据结构】排序算法(下)——插入、希尔、选择、堆、冒泡、快速、归并与计数排序
目录
前言:
排序算法功能接口实现(八大排序算法):
1.插入排序:
①.直接插入排序算法:
2.选择排序:
①.直接选择排序算法:
②.堆排序算法:
3.交换排序:
①.冒泡排序算法:
②.快速排序算法:
4.归并排序(归并排序算法):
5.非比较排序(计数排序算法):
总结:
️博客主页:✈️銮同学的干货分享基地
️欢迎关注:点赞收藏✍️留言
️系列专栏: 数据结构
【进阶】C语言学习
C语言学习
️代码仓库:数据结构仓库
VS2022_C语言仓库
家人们更新不易,你们的点赞和⭐关注⭐真的对我真重要,各位路过的友友麻烦多多点赞关注,欢迎你们的私信提问,感谢你们的转发!
关注我,关注我,关注我,你们将会看到更多的优质内容!!
本文重点 :
八大常见排序算法接口功能实现
前言:
前面我们对八种不同的排序算法的基本思想和实现原理,以及它们各自的算法特性都有了一定的了解,而今天我们将要深入实现插入、希尔、选择、堆、冒泡、快速、归并与计数这八大排序算法各自的接口功能。
排序算法功能接口实现(八大排序算法):
这一部分便是我们今天学习内容的重点,各位小伙伴们务必牢固掌握。
1.插入排序:
①.直接插入排序算法:
接口实现步骤:
- 从第一个元素开始,该元素可以认为已经被排序。
- 取下一个元素 tem,从已排序的元素序列从后向前扫描。
- 如果该元素大于 tem,则将该元素移到下一位。
- 重复步骤 3,直到找到已排序元素中小于或等于 tem 的元素。
- 将 tem 插入到该元素的后面,如果已排序所有元素都大于 tem,则将 tem 插入到下标为 0 的位置。
- 重复步骤 2 ~ 5,直至完成排序。
直接插入排序算法接口代码实现:
void InsertSort(int* arr, int n) { for (int i = 0; i < n - 1; ++i) { int end = i; // 记录有序序列最后一个元素的下标 int tem = arr[end + 1]; // 待插入的元素 while (end >= 0) // 单趟排 { if (tem < arr[end]) // 比插入的数大就向后移 { arr[end + 1] = arr[end]; end--; } else // 比插入的数小,跳出循环 { break; } } arr[end + 1] = tem; // tem放到比插入的数小的数的后面 //代码执行到此位置有两种情况: //1.待插入元素找到应插入位置(break跳出循环到此) //2.待插入元素比当前有序序列中的所有元素都小(while循环结束后到此) } }
②.希尔排序算法:
接口实现步骤:
- 先选定一个小于 N 的整数 gap 作为第一增量,然后将所有距离为 gap 的元素分在同一组,并对每一组的元素进行直接插入排序。然后再取一个比第一增量小的整数作为第二增量,并不断重复上述操作。
- 当增量的大小减到 1 时,就相当于整个序列被分到一组,再进行一次直接插入排序,排序完成。
希尔排序算法接口代码实现:
void ShellSort(int* arr, int n) { int gap = n; while (gap > 1) { gap = gap / 2; // 每次对gap折半操作 for (int i = 0; i < n - gap; ++i) // 单趟排序 { int end = i; int tem = arr[end + gap]; while (end >= 0) { if (tem < arr[end]) { arr[end + gap] = arr[end]; end -= gap; } else { break; } } arr[end + gap] = tem; } } }
2.选择排序:
①.直接选择排序算法:
接口实现步骤:
- 每次从待排序列中选出一个最小值,然后放在序列的起始位置,直到全部待排数据排完即可。
- 实际上,我们可以每次选出两个值,一个最大值一个最小值,然后将其放在序列开头和末尾,这样可以使选择排序的效率提高一倍。
直接选择排序算法接口代码实现:
void swap(int* a, int* b) { int tem = *a; *a = *b; *b = tem; } void SelectSort(int* arr, int n) { int begin = 0, end = n - 1; // 保存参与单趟排序的第一个数和最后一个数的下标 while (begin < end) { int maxi = begin; // 保存最大值的下标 int mini = begin; // 保存最小值的下标 for (int i = begin; i <= end; ++i) // 找出最大值和最小值的下标 { if (arr[i] < arr[mini]) { mini = i; } if (arr[i] > arr[maxi]) { maxi = i; } } swap(&arr[mini], &arr[begin]); // 最小值放在序列开头 if (begin == maxi) // 防止最大的数在begin位置被换走 { maxi = mini; } swap(&arr[maxi], &arr[end]); // 最大值放在序列结尾 ++begin; --end; } }
②.堆排序算法:
接口实现步骤:
- 将小堆的最后一个叶子节点和根节点进行交换。
- 交换后不把最后一个数看作堆里的数据,此时根的左右子树依旧是大堆。
- 再使用向下调整算法选出次小。
- 不断循环这一过程,直到堆里仅剩一个元素(全部排序完成)为止。
堆排序算法接口代码实现(降序):
void AdJustDown(int* a, int n, int parent) { int child = 2 * parent + 1; while (child < n) { //选出两孩子中的较小孩子(需要考虑边界,防止越界访问): if (child + 1 < n && a[child + 1] > a[child]) { ++child; } //向下调整: if (a[child] > a[parent]) { int* tmp = a[child]; a[child] = a[parent]; a[parent] = tmp; parent = child; child = parent * 2 + 1; } else { break; } } } void HeapSort(int* a, int n) { for (int i = (n - 1 - 1) / 2; i >= 0; --i) // 建小堆 { AdjustDown(a, n, i); } int end = n - 1; //把最小的换到最后一个位置,不把最后一个数看作堆里的 //每次选出剩下数中最小的 //从后往前放 while (end > 0) { int tem = a[end]; a[end] = a[0]; a[0] = tem; //选出次小的数 AdJustDown(a, end, 0); --end; } }
3.交换排序:
①.冒泡排序算法:
接口实现步骤:
- 从首元素开始,将每个元素都与后面的其它元素逐一进行比较。
- 比较时将值较大的元素向尾部移动,值较小的元素则向头部移动。
- 对所有元素均进行上述处理即可完成排序。
冒泡排序算法接口代码实现:
//冒泡排序: void BubbleSort(int* arr, int n) { int end = n; while (end) { int flag = 0; for (int i = 1; i < end; ++i) { if (arr[i - 1] > arr[i]) { int tem = arr[i]; arr[i] = arr[i - 1]; arr[i - 1] = tem; flag = 1; } } if (flag == 0) { break; } --end; } }
②.快速排序算法:
Ⅰ.Hoare版本:
接口实现步骤:
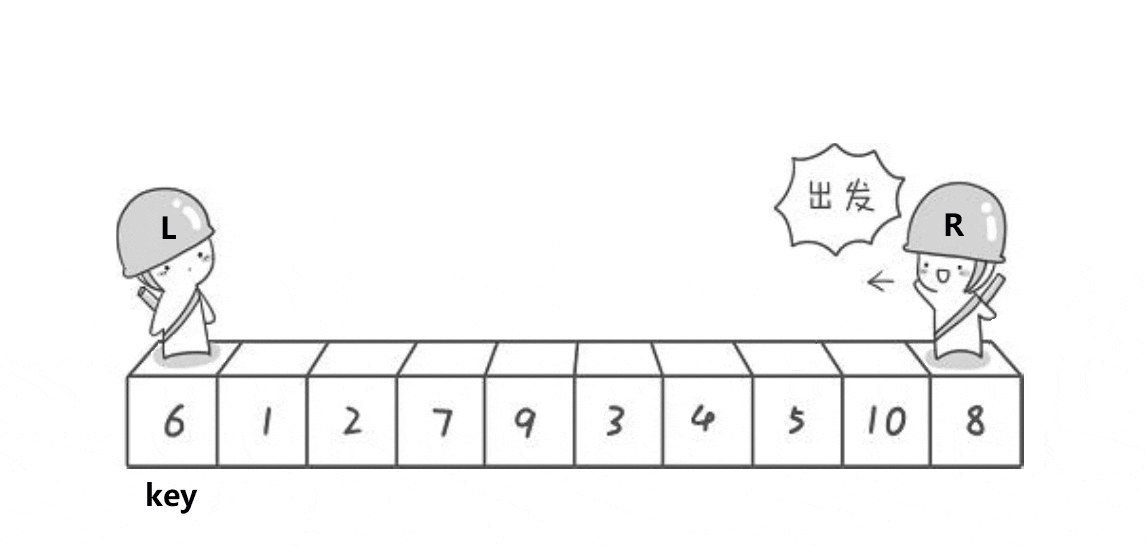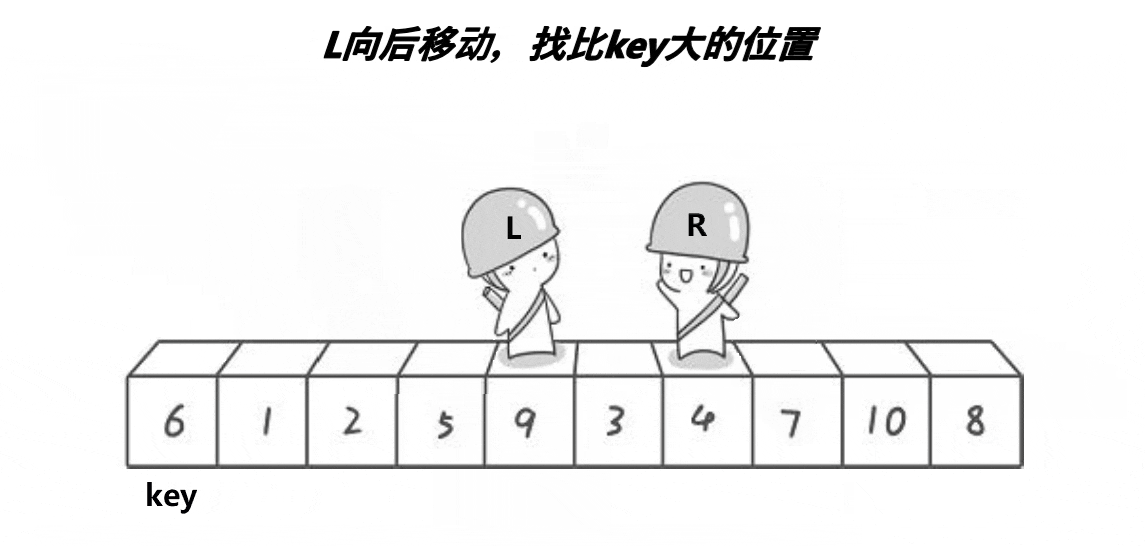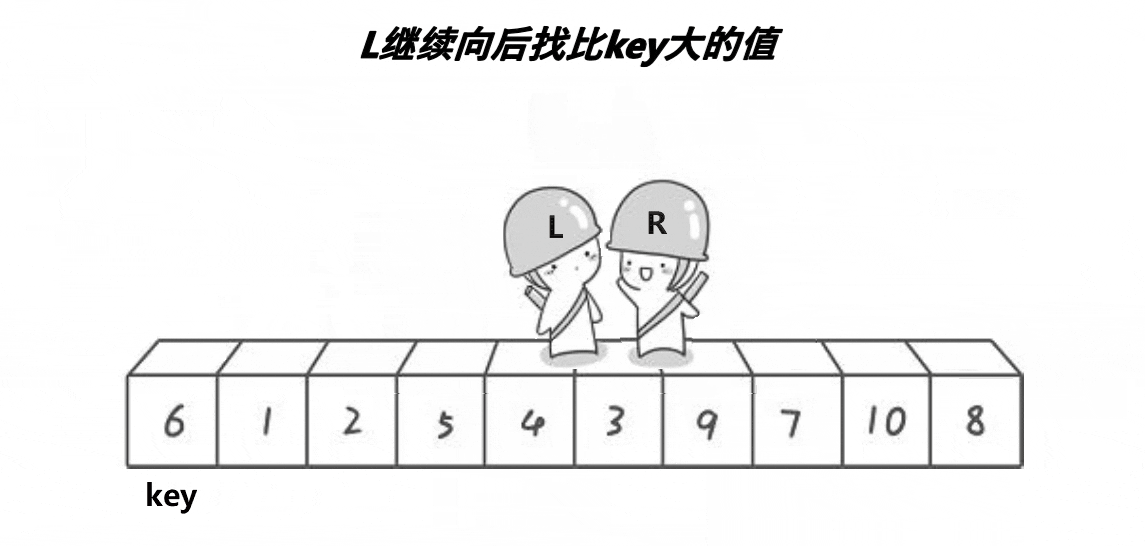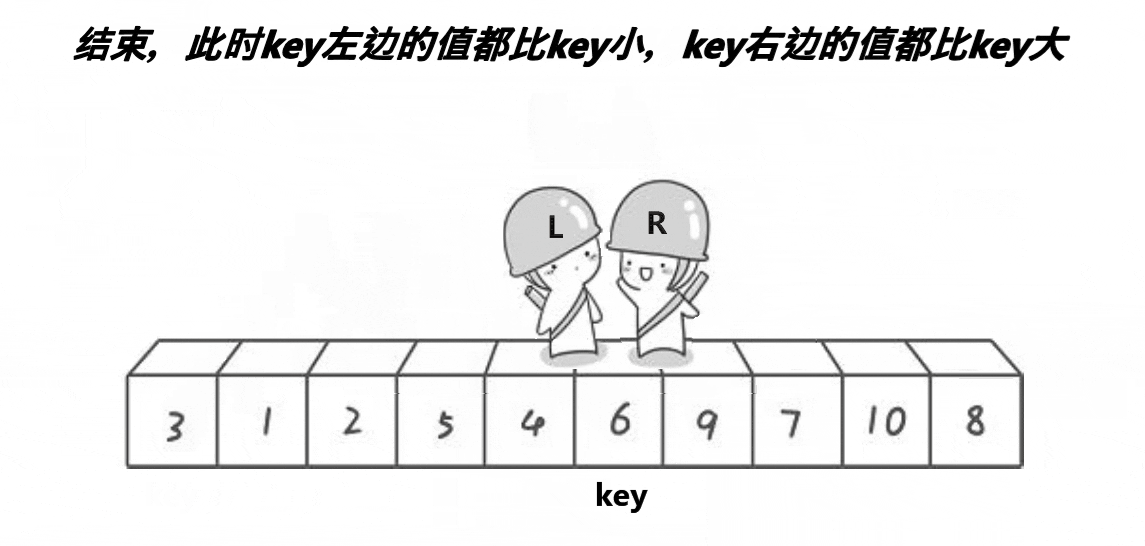
- 选出一个 key,一般最左或最右。
- 定义一个 Left 和一个 right,Left 从左向右走,Right 从右向左走。(需要注意的是:若选择最左边的数据作为 key,则 Right 先走;若选择最右边的数据作为 key,则 Left 先走)。
- 在走的过程中,若 Right 遇到小于 key 的数,则停下,Left 开始走,直到 Left 遇到一个大于 key 的数时,将 Left 和 Right 的内容交换,不断重复这一过程直到 Left 和 Right 相遇为止,此时将相遇点的内容与 key 交换即可。(选取最左边的值作为key)
- 此时 key 的左边都是小于 key 的数,右边都是大于 key 的数。
- 将 key 的左序列和右序列再次进行这种单趟排序,并反复操作,直到左右序列只有一个数据,或是左右序列不存在时,便停止操作,此时此部分已有序。
Hoare 版本快速排序算法接口代码实现:
void swap(int* a, int* b) { int tem = *a; *a = *b; *b = tem; } void QuickSort(int* arr, int begin, int end) { if (begin >= end) // 只有一个数或区间不存在 { printf("QuickSort Error!\n"); return; } int left = begin; int right = end; int keyi = begin; // 选左边为 key while (begin < end) { while (arr[end] >= arr[keyi] && begin < end) // 右边选小,等号防止和key值相等,防止顺序 Left 和 Right 越界 { --end; } while (arr[begin] <= arr[keyi] && begin < end) // 左边选大,等号防止和key值相等,防止顺序 Left 和 Right 越界 { ++begin; } swap(&arr[begin], &arr[end]); // 小的换到右边,大的换到左边 } swap(&arr[keyi], &arr[end]); keyi = end; //[left,keyi-1]keyi[keyi+1,right] QuickSort(arr, left, keyi - 1); QuickSort(arr, keyi + 1, right); }
Ⅱ.挖坑法:
接口实现步骤:
选出一个数据(一般最左或最右)存放在 key 变量中,并在该数据位置形成一个坑。
与 Hoare 版本类似,挖坑法也需要定义一个 Left 和一个 Right,Left 从左向右走,Right 从右向左走。但不同之处在于:若在最左挖坑,则 Right 先走;若在最右挖坑,则 Left 先走。
其余步骤皆与 Hoare 版本无异。
挖坑法有递归与非递归两种实现方式。
挖坑法快速排序算法接口代码实现(递归/非递归):
void QuickSort1(int* arr, int begin, int end) { if (begin >= end) // 只有一个数或区间不存在 { printf("QuickSort Error!\n"); return; } int left = begin, right = end; int key = arr[begin]; while (begin < end) { while (arr[end] >= key && begin < end) // 找小值 { --end; } arr[begin] = arr[end]; // 小值放进左坑 while (arr[begin] <= key && begin < end) // 找大值 { ++begin; } arr[end] = arr[begin]; // 大值放进右坑 } arr[begin] = key; int keyi = begin; //[left,keyi-1]keyi[keyi+1,right] QuickSort1(arr, left, keyi - 1); QuickSort1(arr, keyi + 1, right); }//(非递归)挖坑法快速排序算法: int PartSort(int* arr, int begin, int end) { int key = arr[begin]; while (begin < end) { while (key <= arr[end] && begin < end) { --end; } arr[begin] = arr[end]; while (key >= arr[begin] && begin < end) { ++begin; } arr[end] = arr[begin]; } arr[begin] = key; int meeti = begin; return meeti; } void QuickSortNoR(int* arr, int begin, int end) { stackst; st.push(end); // 先入右边 st.push(begin); // 再入左边 while (!st.empty()) { int left = st.top(); // 左区间 st.pop(); int right = st.top(); // 右区间 st.pop(); int mid = PartSort(arr, left, right); // 中间数 if (left < mid - 1) // 左区间 >= mid-1,则说明左区间已排好 { st.push(mid - 1); st.push(left); } if (right > mid + 1) // mid+1 >= 右区间,则说明右区间已排好 { st.push(right); st.push(mid + 1); } } }
Ⅲ.前后指针法:
接口实现步骤:
选出一个 key,一般最左或最右。
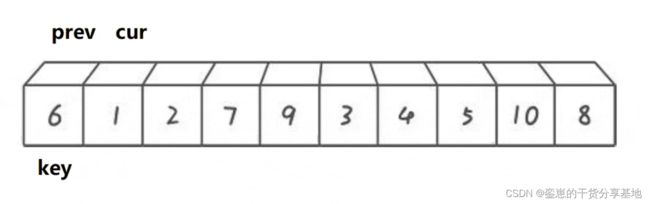
起始时,prev 指针指向序列开头,cur 指针指向 prev+1 (prev 后元素)。
若 cur 指向的内容小于 key,则 prev 先向后移动一位,然后交换 prev 和 cur 指针指向的内容,然后 cur 指针后移一位;若 cur 指向的内容大于 key ,则 cur 指针直接后移。如此反复进行下去,直到 cur 到达 Right 位置,此时将 key 和 ++prev 指针指向的内容交换即可。
经过一次单趟排序,可以使 key 左边的数据全部都小于 key,key 右边的数据全部都大于key。
与前两种方法相同,还是将 key 的左序列和右序列重复进行这种单趟排序,直到左右序列只有一个数据,或是左右序列不存在时,停止操作。
前后指针法快速排序算法接口代码实现:
void QuickSort2(int* arr, int begin, int end) { if (begin >= end) // 只有一个数或区间不存在 { printf("QuickSort Error!\n"); return; } int cur = begin, prev = begin - 1; int keyi = end; while (cur != keyi) { if (arr[cur] < arr[keyi] && ++prev != cur) { swap(&arr[cur], &arr[prev]); } ++cur; } swap(&arr[++prev], &arr[keyi]); keyi = prev; //[begin,keyi -1]keyi[keyi+1,end] QuickSort2(arr, begin, keyi - 1); QuickSort2(arr, keyi + 1, end); }
4.归并排序(归并排序算法):
接口实现步骤:
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列。
设定两个指针,初始位置为两个已排序序列的起始位置。
比较两指针指向元素,选择相对小的元素放入到合并空间,并移动指针到下一位置。
重复步骤 3 直到某一指针达到序列尾。
将另一序列剩下的所有元素直接复制到合并序列尾。
归并排序算法接口代码实现:
private static void merge(int[] arr, int L, int M, int R) { int[] help = new int[R - L + 1]; // 设置辅助空间 int i = 0; int p1 = L; int p2 = M + 1; while (p1 <= M && p2 < R) // 判断两边值是否越界 { help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++]; // 当左值<右值时,将左值拷贝进help;否则将右值拷贝到进help } while (p1 <= M) // 如果p1没有越界,那么将p1剩下的东西全部拷贝进help { help[i++] = arr[p1++]; } while (p2 <= R) // 如果p2没有越界,那么将p2剩下的东西全部拷贝进help { help[i++] = arr[p2++]; } for (i = 0; i < help.length; i++) { arr[L + i] = help[i]; } }
5.非比较排序(计数排序算法):
接口实现步骤:
- 找出待排序的数组中最大和最小的元素。
- 统计数组中每个值为 i 的元素出现的次数,存入数组 C 的第 i 项。
- 对所有的计数累加(从 C 中的第一个元素开始,每一项和前一项相加)。
- 反向填充目标数组:将每个元素 i 放在新数组的第 C(i) 项,每放一个元素就将 C(i) 减1。
计数排序算法接口代码实现:
void count_sort(int* arr, int* sorted_arr, int n) { int* count_arr = (int*)malloc(sizeof(int) * 100); int i; for (i = 0; i < 100; i++) // 初始化计数数组 { count_arr[i] = 0; } for (i = 0; i < n; i++) // 统计i的次数 { count_arr[arr[i]]++; } for (i = 1; i < 100; i++) // 对所有的计数累加 { count_arr[i] += count_arr[i - 1]; } for (i = n; i > 0; i--) // 逆向遍历源数组(保证稳定性),根据计数数组中对应的值填充到先的数组中 { sorted_arr[count_arr[arr[i - 1]] - 1] = arr[i - 1]; count_arr[arr[i - 1]]--; } free(count_arr); count_arr = NULL; }
总结:
今天我们完成了八大常用排序算法各自的实现,小伙伴们一定要熟练掌握这八种最重要的排序算法。并且除了这八种算法之外,仍有许多更加优秀,更加贴合实例的排序算法等待我们去发掘。至此,我们初阶数据结构的相关知识讲解就到此为止了,高阶数据结构的内容銮崽将在为大家介绍 C++ 的相关时继续讲解,各位铁铁们敬请期待多多支持哟。各位小伙伴们在学习和工作中也一定要不断学习,不断充实自我,为自己美好光明的未来而奋斗!
坚持意志伟大的事业需要始终不渝的精神
更新不易,辛苦各位小伙伴们动动小手,三连走一走 ~ ~ ~ 你们真的对我很重要!最后,本文仍有许多不足之处,欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正!