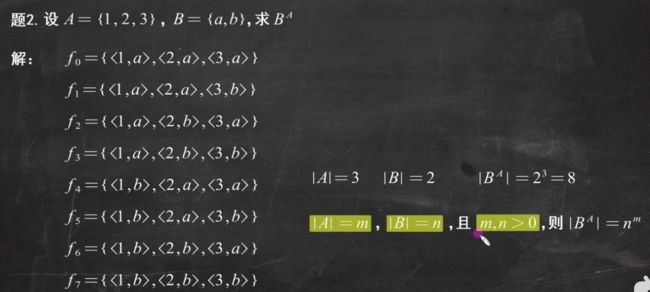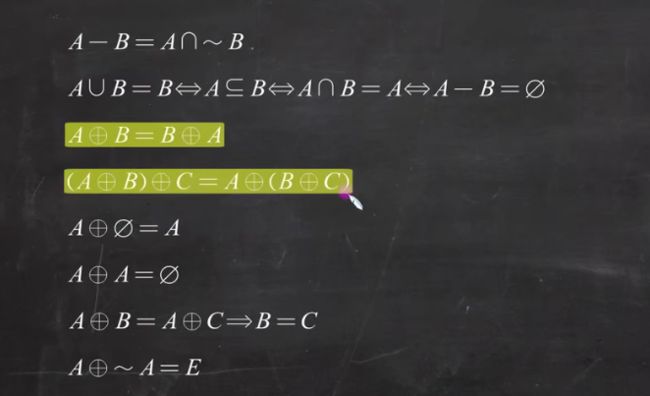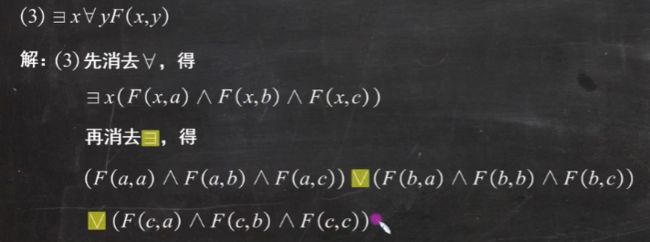离散数学期末复习
文章目录
-
- 二元关系
-
- 0:自反对称传递
- 1:商集
- 2:集合的划分
- 3:求等价关系
- 4:等价关系的求证
- 5:偏序关系的求证,画哈斯图
- 6:偏序关系的最大元与最小元
- 7:偏序关系中的极大元与极小元。
- 8:偏序关系的上界和上确界,下界下确界
- 函数
-
- 1:函数的满射单射与双射
- 2:函数的复合运算
- 3:反函数
- 课后习题
- 图
-
- 1:基本概念
- 2:有向图和无向图的度数
- 3:握手定理
- 4:出度序列与入度序列
- 5:最大度与最小度
- 6:判断数列是否可图化
- 7:无向完全图
- 8:通路与回路
- 8:图的连通性
- 9:图的矩阵表示
-
- 有向图的关联矩阵
- 有向图的邻接矩阵
- 根据矩阵求通路数
- 可达矩阵
- 欧拉图与哈密顿图
-
-
- 哈密顿图
- 最短路问题
- 习题
-
- 树
-
- 无向树及其性质
- 最小生成树
- 画最小生成树与权总和
- 根数及其应用
- 哈夫曼算法计算权重与权值。
- 最佳前缀码
-
- 最优二叉树与最佳前缀码
- 题目
- 平面图
-
- 概念
-
- 性质
- 欧拉公式:连通平面图:
- 练习题
- 集合代数
-
- 基本概念
- 对称差
- 包含排斥定理
- 集合恒等式
- 习题:
- 命题逻辑
-
- 概念
- 命题连接词
- 命题符号化重点
- 命题公式及其赋值
-
- 求成真赋值与成假赋值
-
- 优先顺序 () —— ∩ ∪ ➡ ⬅➡
- 重言式与矛盾式
- 习题:
- 命题逻辑等值演算
-
- 等值式
- 常见等值式
- 一个例题
- 析取范式与合取范式
- 求析取和合取范式
- 主析取范式与主合取范式
-
- 极小项与最大项
- 真值表法
- 例题
- 谓词逻辑基本概念
-
- 谓词逻辑命题符号化
- 量词:全称量词与存在量词
- 有人登上月球
- 指导变元,约束出现
- 谓词逻辑的永真与矛盾式
- 谓词逻辑等值式与置换规则
-
- 等值式
- 公式:量词辖域收缩与扩张等值式
- 量词分配等值式
- 全称量词与合取搭配
- 谓词逻辑前束范式
- 量词消去规则
二元关系
0:自反对称传递
1:商集
2:集合的划分
集合不含空集,两集合的交集也为空集,两集合的并集为A,则为A的一个划分。
3:求等价关系
有多少种划分就有多少种等价关系
下图对应的都是恒等关系:
4:等价关系的求证
若xy属于T则有xy属于R且yx属于r。
5:偏序关系的求证,画哈斯图
如果R是自反的,反对称的和传递的,则R为A上的偏序关系。
6:偏序关系的最大元与最小元
最大元:找到最上面的一个元素与其他元素都有线段连接
最小元:找到元素要小于等于集合中的任何元素,且可比(有关系)
最大元与最小元的前提都是可比的,如果元素与元素之间没有关系,也就是不可比,则不是最大元与最小元。
下图中23不可比,所以都不是最小元
7:偏序关系中的极大元与极小元。
孤立的点也可以叫极大元?
极大元:没有比极大元更大的元素,只需要找谁在最上面
极小元:没有比极小元更小的元素,只需要找谁在最下面
不需要满足可比性
8:偏序关系的上界和上确界,下界下确界
比子集大的A中元素都为上界
大的恰到好处不能再少的,为上确界。
同时求上界与上确界需要满足可比,23不可比,所以3不能是上界
下界:比子集小的A中元素都为下界
下确界:下的恰到好处,是下界中的最大
题目:有空就做:
函数
一个x不能对应两个y
1:函数的满射单射与双射
2:函数的复合运算
<1,2>与<2,3>复合为<1,3>,<1,2>不能与<3,3>复合。
3:反函数
课后习题
图
1:基本概念
如图e2的关联为v1与v2,关联数为2
无向图有共同边连接的两个顶点是相邻的
相邻:有向边的两个顶点之间是相邻的,但是必须一条边的终点是另一条边的起点,才能说两条边相邻。
2:有向图和无向图的度数
无向图顶点度数的计算包括起始点和终点,无向图一条边算一度,但是如果是自环,则算两度
3:握手定理
4:出度序列与入度序列
5:最大度与最小度
度数之和要为偶数
6:判断数列是否可图化
1:一定为偶数,最大度小于等于n-1,不能为4,所以选d。
7:无向完全图
定义:
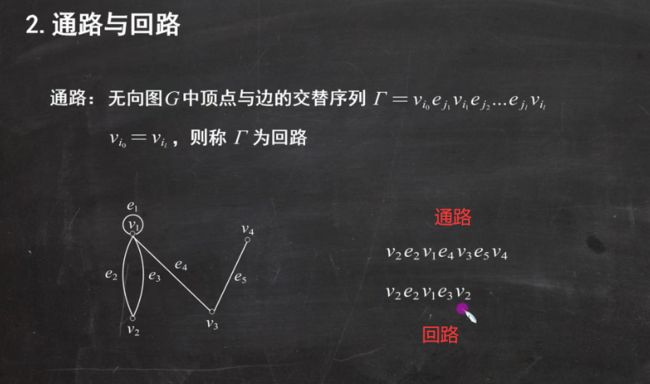
8:通路与回路
定义:顶点边顶点边的交替形式称为回路,没有孤立的点
第一个顶点与最后一个顶点相同为通路,有环且没有孤立 的顶点
8:图的连通性
任何两个顶点联通
9:图的矩阵表示
行对应顶点个数,列对应边的个数。如果顶点重合关联次数为2,顶点不重合,关联次数为1.
有向图的关联矩阵
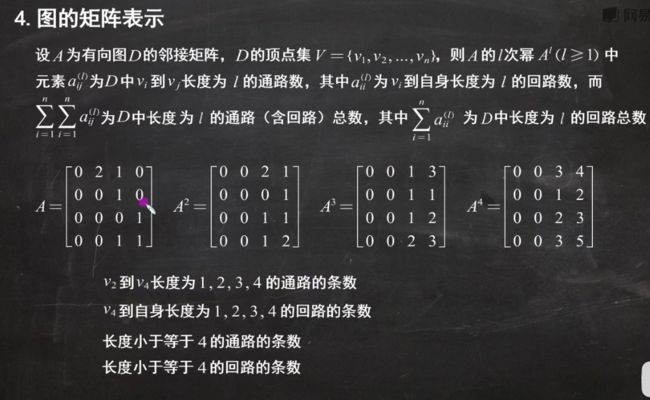
有向图的邻接矩阵
顶点到顶点边的条数
根据矩阵求通路数
长度为1在A1中找长度为2在A^2中找
回路看对角线长度为1的元素
可达矩阵
任何一个元素到达自身都是可达的,所以可达矩阵主对角线上的元素全为1
欧拉图与哈密顿图
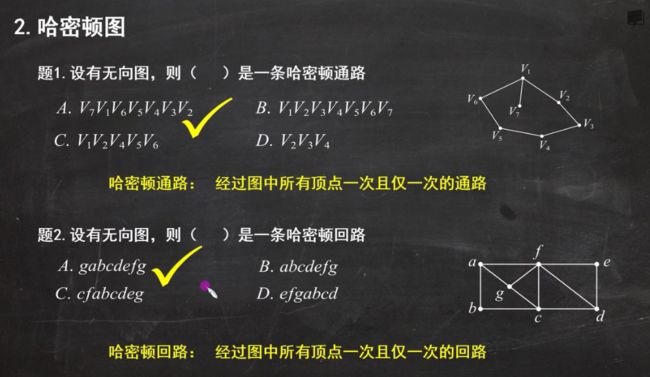
哈密顿图
判断是否存在哈密顿通路:任意两个不相邻顶点的度数大于等于n-1
是否存在哈密顿回路:任意两个不相邻顶点大于n
最短路问题
图中有数字的图叫带权图。
长度就是指权。
迪杰特斯拉算法。顶点到自身的距离看为0,顶点到不相邻点的距离看为∞,然后一直找相邻的距离最小的顶点。
注意是求V1到其余各点
习题
树
无向树:没有环,单连通。树叶:度数等于1的顶点。
平凡图:途中只有一个顶点且没有边
无向树及其性质
握手定理:所有顶点的度数之和等于边数的两倍。树的边数又等于顶点数减一
最小生成树
无向图有生成树当且仅当G是连通图
画最小生成树与权总和
根数及其应用
基图:讲有向树的箭头省去就变成了无向树。根树就是树根。
v1是v5、v8的祖先,v5是v1的后代。
相邻则是父子关系。v8与v9是兄弟关系。
权总和:结点的权值乘以权重
哈夫曼算法计算权重与权值。
最佳前缀码
比如集合中的元素adc,在此集合中可找到a或ad则不能构成前缀码。
A选项中,aa与aaa矛盾。如果是aa找有没有单个a,如果是aba,找有没有单个ab,adc找有没有单个的a或ad
最优二叉树与最佳前缀码
题目
平面图
概念
二部图:上面的顶点必须与下面的所有顶点进行相连。
平面图:除了顶点之外没有边进行相交。如果通过将边往外拉可以不相交,依然可以称为平面图
k5代表顶点为5的完全图,k33代表顶点为3的完全二部平面图。
性质
平面图所有面的次数之和等于边数的两倍。
欧拉公式:连通平面图:
顶点数-边数+面数=2
练习题
集合代数
基本概念
对称差
(A-B)∪(B-A) ~A表示A的补集
![]()
包含排斥定理
||表示元素的个数
集合恒等式
集合证明:
习题:
命题逻辑
概念
命题连接词
否定合取、析取、蕴涵(→)等价(⬅➡)
蕴含:前真后假才为假。等价,同时为0或同时为1为真。
命题符号化重点
排斥或
命题公式及其赋值
pqr都是既可以取0又可以取1,则都是命题变元。
成真赋值:真值为1 的时候pq的取值
成假赋值:真值为0的时候pq的取值。
求成真赋值与成假赋值
优先顺序 () —— ∩ ∪ ➡ ⬅➡
重言式与矛盾式
重言式:在各种情况下都为真为重言式也叫永真式。
矛盾式:在各种情况下取址均为假叫永假式也叫矛盾式。
不是矛盾式,则是可满足式。
习题:
命题逻辑等值演算
等值式
常见等值式
一个例题
析取范式与合取范式
析取范式:由有限个简单合取式的析取构成的命题式。
合取范式:由简单析取式的合取构成的范式。
求析取和合取范式
析取范式:只需要把式子化成括号里面都是合取,括号外面都是析取就可以啦。
主析取范式与主合取范式
极小项与最大项
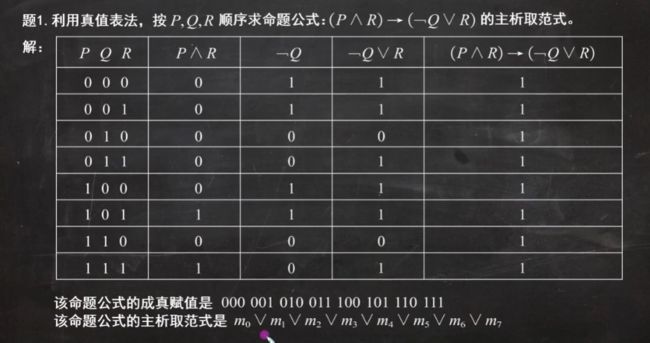
真值表法
例题
连接词的完备集
谓词逻辑基本概念
谓词逻辑命题符号化
量词:全称量词与存在量词
![]()
有人登上月球
人和月球有交叉。如果时蕴含,则变成了,如果他是人则他一定登上过月球。
存在量词用析取,全称量词用蕴含
指导变元,约束出现
指导变元都约束出现。
谓词逻辑的永真与矛盾式
谓词逻辑等值式与置换规则
等值式
公式:量词辖域收缩与扩张等值式
量词分配等值式
全称量词与合取搭配
消去存在量词加析取,消去全称量词加合取
谓词逻辑前束范式
将量词放在括号外
![]()