基于相机模型的单目测距--普通相机
文章目录
-
- 一、相机模型原理
-
-
- 1、像素坐标系(u,v)至图像坐标系(x,y)
- 2、图像坐标系(x,y)至相机坐标系(Xc,Yc,Zc)
- 3、相机坐标系(Xc,Yc,Zc)至世界坐标系(Xw,Yw,Zw)
- 4、像素坐标系(u,v)与世界坐标系(Xw,Yw,Zw)的总关系式
-
- 二、OpenCV 相机标定
- 三、根据内参推导像素坐标(u, v)与图像坐标(x, y)的关系式
- 四、根据内参和畸变系数测量外参
- 五、根据内参和外参推导图像坐标与世界坐标的关系式
- 法一:根据外参和世界坐标点计算距离
- 法二:根据焦距和世界坐标点计算距离
一、相机模型原理
在视觉测量中,需要进行的一个重要预备工作是定义四个坐标系的意义,即 像素坐标系 、 图像坐标系、 相机坐标系 和 世界坐标系(参考坐标系),其中像素坐标系以像素为单位,其它三种坐标系以毫米mm为单位,下图把世界坐标系和相机坐标系以m为单位,我认为是不对的,因为我整个测量过程中物理单位始终是mm单位,但下图总述了相机模型的整体模型关系,所以贴了下来。
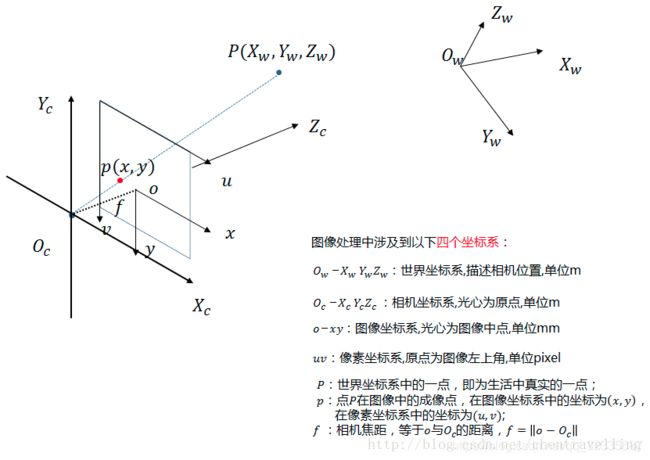
下面是关于这几个坐标系的转换。** 叙述思路从像素坐标系一步一步转换到世界坐标系,意味着如何从一个像素点获得世界坐标系的坐标点,从而可以进行实际距离测量 **。
1、像素坐标系(u,v)至图像坐标系(x,y)
当两个坐标轴互相垂直时,可以得到两者的关系表达式:
 图像坐标系的单位是mm,属于物理单位,而像素坐标系的单位是pixel,我们平常描述一个像素点都是几行几列。所以这二者之间的转换如下:其中dx和dy表示每一列和每一行分别代表多少mm,即1pixel=dx mm
图像坐标系的单位是mm,属于物理单位,而像素坐标系的单位是pixel,我们平常描述一个像素点都是几行几列。所以这二者之间的转换如下:其中dx和dy表示每一列和每一行分别代表多少mm,即1pixel=dx mm
2、图像坐标系(x,y)至相机坐标系(Xc,Yc,Zc)
根据三角形相似性原理得:
 (根据小孔成像原理,图像坐标系应在相机坐标系的另一边,为倒立反向成像,但为方便理解和计算,故投影至同侧。)
(根据小孔成像原理,图像坐标系应在相机坐标系的另一边,为倒立反向成像,但为方便理解和计算,故投影至同侧。)
3、相机坐标系(Xc,Yc,Zc)至世界坐标系(Xw,Yw,Zw)
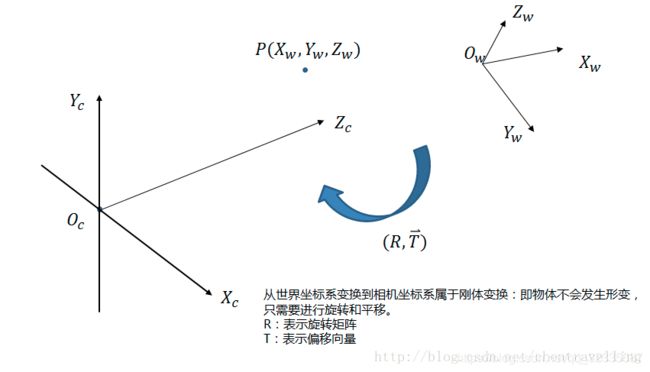 于是,从世界坐标系到相机坐标系,涉及到旋转和平移(其实所有的运动也可以用旋转矩阵和平移向量来描述)。绕着不同的坐标轴旋转不同的角度,得到相应的旋转矩阵,如下图所示:
于是,从世界坐标系到相机坐标系,涉及到旋转和平移(其实所有的运动也可以用旋转矩阵和平移向量来描述)。绕着不同的坐标轴旋转不同的角度,得到相应的旋转矩阵,如下图所示:
 那么从世界坐标系到相机坐标系的转换关系如下所示:
那么从世界坐标系到相机坐标系的转换关系如下所示:

4、像素坐标系(u,v)与世界坐标系(Xw,Yw,Zw)的总关系式
 其中M1称为相机的内参矩阵,包含内参(fx,fy,u0,v0)。M2称为相机的外参矩阵,包含外参(R:旋转矩阵3×3,T:平移矩阵3×1)
其中M1称为相机的内参矩阵,包含内参(fx,fy,u0,v0)。M2称为相机的外参矩阵,包含外参(R:旋转矩阵3×3,T:平移矩阵3×1)
相机模型原理参考:
计算机视觉:相机成像原理:世界坐标系、相机坐标系、图像坐标系、像素坐标系之间的转换
最详细、最完整的相机标定讲解
二、OpenCV 相机标定
相机标定目的是为了得到相机的内参参数和畸变系数
1、找到标定例程
在OpenCV安装目录下,进入samples/cpp/tutorial_code/calib3d/camera_calibration目录,拷贝一份到其它位置
2、修改标定配置参数
找到camera_calibration/in_VID5.xml文件,这是标定程序使用的配置文件,需要设置里面的几个参数。
2.1、设置棋盘格的尺寸,采用宽度为9,高度为6的棋盘格:
<BoardSize_Width>9BoardSize_Width>
<BoardSize_Height>6BoardSize_Height>
 需要特别注意的是,这里的宽度和高度是指内部交叉点的个数,而不是方形格的个数。如下图所示的棋盘格,内部交叉点的宽度是9,高度是6。请务必填写正确,否则无法标定。
需要特别注意的是,这里的宽度和高度是指内部交叉点的个数,而不是方形格的个数。如下图所示的棋盘格,内部交叉点的宽度是9,高度是6。请务必填写正确,否则无法标定。
2.2、设置棋盘格的宽度
每格的宽度应设置为实际的毫米数,该参数的实际用途尚待考证。目前看来,即使设置的不准确也无大碍。我使用1:1的比例用A4纸打印出来测到每格宽度为22mm。
<Square_Size>22Square_Size>
2.3、选择输入方式
例程提供了三种输入方式。不过,如果待标定的摄像头已经接入电脑,建议使用input camera方式。该方式只需要设置视频输入设备号,我的是外接摄像头,即设备号为0。
<Input>"0"Input>
3、编译
新建camera_calibration/CMakeLists.txt文件,写入如下内容。
cmake_minimum_required(VERSION 2.8.7)
project(Camera_Calibration)
set(CMAKE_CXX_STANDARD 11)
find_package(OpenCV REQUIRED)
add_executable(Camera_Calibration camera_calibration.cpp)
target_link_libraries(Camera_Calibration ${OpenCV_LIBS})
编译
mkdir build
cd build
cmake ..
make
4、运行
运行时需要传入配置文件作为主函数的参数:
./Camera_Calibration ../in_VID5.xml
程序启动后会出现当前摄像头拍摄到的画面,画面里有操作提示。按下键盘’g’键开始标定。请务必使摄像头从不同方向拍摄棋盘格,以保证程序准确计算图像畸变。

共拍摄25张照片后自动结束标定,标定结果写入
camera_calibration/out_camera_data.xml。
这里有一些注意事项:
(1) 要在上下左右各个角度拍摄棋盘格,以减少各个图片间的相关性,有利于求解相机参数和畸变系数。
(2) 由于普通相机的畸变不大,所以相机标定后的图像应该保持正常,不会产生畸变才是正确的(这点是否正确,有待考证!),我标定后的图像与标定前差别不大,平均误差为0.57,最后计算外参得到的相机位姿坐标的误差为10mm之内
相机标定参考:opencv相机标定
三、根据内参推导像素坐标(u, v)与图像坐标(x, y)的关系式
根据像素坐标系与图像坐标系的关系式:
u = x / d x + u 0 u = x/dx + u0 u=x/dx+u0 v = y / d y + v 0 v = y/dy + v0 v=y/dy+v0 f x = F c / d x fx = Fc / dx fx=Fc/dx f y = F c / d y fy = Fc / dy fy=Fc/dy
联合上式,可得:
x = ( u − u 0 ) ∗ ( F c / f x ) x = (u - u0) * (Fc / fx) x=(u−u0)∗(Fc/fx) y = ( v − v 0 ) ∗ ( F c / f y ) y = (v - v0) * (Fc / fy) y=(v−v0)∗(Fc/fy)
其中 F c Fc Fc为焦距, f x , f y , u 0 , v 0 fx,fy,u0,v0 fx,fy,u0,v0为相机内参参数, d x , d y dx,dy dx,dy分别为x轴和y轴的尺度因子
四、根据内参和畸变系数测量外参
1、准备好四个特征点的世界坐标,存入Mat矩阵
vector Points3D;
Points3D.push_back(cv::Point3f(0, 0, 0)); //P1 三维坐标的单位是毫米
Points3D.push_back(cv::Point3f(0, 200, 0)); //P2
Points3D.push_back(cv::Point3f(150, 0, 0)); //P3
Points3D.push_back(cv::Point3f(150, 200, 0)); //P4
2、.准备好四个特征点在图像上的对应点坐标,这个像素坐标在实验中我是获取鼠标坐标得到的,目的是为了操作方便。注意,输入坐标的顺序一定要与之前输入世界坐标的顺序一致,就是说世界坐标点与像素点要一一对应上。
vector Points2D; //四个特征点在图像上的对应点坐标的向量
void onMouse(int event, int x, int y, int flags, void* param)
{
cv::Mat im = *(cv::Mat*)param;
switch(event)
{
case CV_EVENT_LBUTTONDOWN:
{
Points2D.push_back(cv::Point2f(x, y));
cv::circle(im, cv::Point(x, y), 2, cv::Scalar(0, 0, 255), 3);
cout<<"x = "<< x << " " <<"y = "<< y << endl;
}
break;
case CV_EVENT_RBUTTONDOWN:
cout << "Please use left BUTTON" << endl;
break;
}
}
但采用鼠标获取坐标势必会增加坐标值的误差,建议采用下面参考链接[2]Opencv:SolvePNP的方法,可以减少手动鼠标选取像素坐标的人为误差,通过查找四个点的轮廓,计算出轮廓质心得到图像上四个点的像素坐标,再通过它们在图像下的相对位置进行排序,最终与世界坐标点一一对应上。
//计算轮廓矩
vector mu(contours.size());
for (int i = 0; i < contours.size(); i++)
{
mu[i] = moments(contours[i], false);
}
//计算轮廓的质心
vector mc(contours.size());
for (int i = 0; i < contours.size(); i++)
{
mc[i] = Point2d(mu[i].m10 / mu[i].m00, mu[i].m01 / mu[i].m00);
//points[0].push_back(mc[i]);
dis[i] = sqrt(double(mc[i].x * mc[i].x + mc[i].y * mc[i].y));
dis_x[i] = mc[i].x;
dis_y[i] = mc[i].y;
//cout << "第" << i << "个轮廓中心为" << mc[i].x << "\t" << mc[i].y << endl;
}
3、使用pnp解算求出相机旋转矩阵与平移矩阵
//初始化输出矩阵
cv::Mat rvec = cv::Mat::zeros(3, 1, CV_64FC1);
cv::Mat tvec = cv::Mat::zeros(3, 1, CV_64FC1);
//三种方法求解
//solvePnP(Points3D, Points2D, camera_matrix, distortion_coefficients, rvec, tvec, false, CV_ITERATIVE); //实测迭代法似乎只能用共面特征点求位置
solvePnP(Points3D, Points2D, camera_matrix, distortion_coefficients, rvec, tvec, false, CV_P3P); //Gao的方法可以使用任意四个特征点
//solvePnP(Points3D, Points2D, camera_matrix, distortion_coefficients, rvec, tvec, false, CV_EPNP);
//旋转向量变旋转矩阵
double rm[9];
cv::Mat rotM(3, 3, CV_64FC1, rm);
Rodrigues(rvec, rotM);
solvePNP函数介绍
void solvePnP(InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess=false, int flags = CV_ITERATIVE)
Parameters:
- objectPoints - 世界坐标系下的控制点的坐标,vector的数据类型在这里可以使用
- imagePoints - 在图像坐标系下对应的控制点的坐标。vector在这里可以使用
- cameraMatrix - 相机的内参矩阵
- distCoeffs - 相机的畸变系数
- rvec - 输出的旋转向量。使坐标点从世界坐标系旋转到相机坐标系
- tvec - 输出的平移向量。使坐标点从世界坐标系平移到相机坐标系
- flags - 默认使用CV_ITERATIV迭代法
4、根据旋转矩阵和平移矩阵求出深度信息(本文章就是借鉴这个思路计算距离的,下面会讲)
P c a m = R ∗ P w o r l d + T Pcam = R * Pworld + T Pcam=R∗Pworld+T P c a m Pcam Pcam 代表物体在相机坐标系下的坐标, P w o r l d Pworld Pworld 代表物体在世界坐标系下的坐标, R R R 和 T T T 代表了将目标点从世界坐标系下转换到相机坐标系下,可以知道solvePnP求出的刚好是这样的映射关系。
使 P c a m = 0 Pcam = 0 Pcam=0,则意味着物体移到了相机坐标系的原点,求出来的 P w o r l d Pworld Pworld代表了相机坐标系原点在世界坐标系中的位置。如果相机摆放在四个特征点的P1与P2的连线方向,那么 P w o r l d Pworld Pworld的y轴坐标就是深度信息;如果相机摆放在四个特征点的P1与P3的连线方向,那么 P w o r l d Pworld Pworld的x轴坐标就是深度信息。
0 = P R + T 0=PR+T 0=PR+T P = − i n v e r s e ( R ) ∗ T P = -inverse(R)*T P=−inverse(R)∗T
5、实际测量过程图片参照链接[1],这里偷偷懒,有空再补上
相机外参测量参考:
[1] 根据四个特征点估计相机姿态
[2] Opencv:SolvePNP
五、根据内参和外参推导图像坐标与世界坐标的关系式
注意:单目测距失去了空间信息,这里是基于世界平面坐标的前提
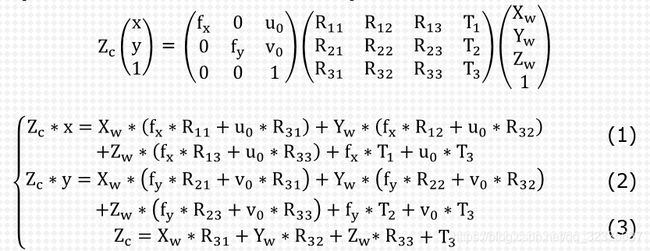
把(3)式代入(1)(2)式,可以得到 图像坐标与世界坐标的关系式 :
X w ∗ ( f x ∗ R 11 + u 0 ∗ R 31 − x ∗ R 31 ) + Y w ∗ ( f x ∗ R 12 + u 0 ∗ R 32 − x ∗ R 32 ) + Z w ∗ ( f x ∗ R 13 + u 0 ∗ R 33 − x ∗ R 33 ) = T 3 ∗ x − f x ∗ T 1 − u 0 ∗ T 3 Xw * ( fx * R11 + u0 * R31 - x * R31) + Yw * (fx * R12 + u0 * R32 - x * R32) + Zw * (fx * R13 + u0 * R33 - x * R33) = T3 * x - fx * T1 - u0 * T3 Xw∗(fx∗R11+u0∗R31−x∗R31)+Yw∗(fx∗R12+u0∗R32−x∗R32)+Zw∗(fx∗R13+u0∗R33−x∗R33)=T3∗x−fx∗T1−u0∗T3 X w ∗ ( f y ∗ R 21 + v 0 ∗ R 31 − y ∗ R 31 ) + Y w ∗ ( f y ∗ R 22 + v 0 ∗ R 32 − y ∗ R 32 ) + Z w ∗ ( f y ∗ R 23 + v 0 ∗ R 33 − y ∗ R 33 ) = T 3 ∗ y − f y ∗ T 2 − v 0 ∗ T 3 Xw * ( fy * R21 + v0 * R31 - y * R31)+ Yw * (fy * R22 + v0 * R32 - y * R32) + Zw * (fy * R23 + v0 * R33 - y * R33) = T3 * y - fy * T2 - v0 * T3 Xw∗(fy∗R21+v0∗R31−y∗R31)+Yw∗(fy∗R22+v0∗R32−y∗R32)+Zw∗(fy∗R23+v0∗R33−y∗R33)=T3∗y−fy∗T2−v0∗T3
由于基于世界平面坐标的考虑,所以世界坐标系的Z轴为0,即 Z w = 0 Zw=0 Zw=0,代入图像坐标与世界坐标的关系式,简化可得 图像坐标与世界平面坐标的关系式 :
X w ∗ ( f x ∗ R 11 + u 0 ∗ R 31 − x ∗ R 31 ) + Y w ∗ ( f x ∗ R 12 + u 0 ∗ R 32 − x ∗ R 32 ) = T 3 ∗ x − f x ∗ T 1 − u 0 ∗ T 3 Xw * ( fx * R11 + u0 * R31 - x * R31) + Yw * (fx * R12 + u0 * R32 - x * R32) = T3 * x - fx * T1 - u0 * T3 Xw∗(fx∗R11+u0∗R31−x∗R31)+Yw∗(fx∗R12+u0∗R32−x∗R32)=T3∗x−fx∗T1−u0∗T3 X w ∗ ( f y ∗ R 21 + v 0 ∗ R 31 − y ∗ R 31 ) + Y w ∗ ( f y ∗ R 22 + v 0 ∗ R 32 − y ∗ R 32 ) = T 3 ∗ y − f y ∗ T 2 − v 0 ∗ T 3 Xw * ( fy * R21 + v0 * R31 - y * R31) + Yw * (fy * R22 + v0 * R32 - y * R32) = T3 * y - fy * T2 - v0 * T3 Xw∗(fy∗R21+v0∗R31−y∗R31)+Yw∗(fy∗R22+v0∗R32−y∗R32)=T3∗y−fy∗T2−v0∗T3
其中 ( x , y ) (x,y) (x,y)表示图像坐标系下的目标点坐标, ( X w , Y w ) (Xw,Yw) (Xw,Yw)表示世界平面坐标系下的目标点坐标, f x , f y , u 0 , v 0 fx,fy,u0,v0 fx,fy,u0,v0为相机内参参数, R 和 T R和T R和T为相机外参参数
法一:根据外参和世界坐标点计算距离
P c a m = R ∗ P w o r l d + T Pcam = R * Pworld + T Pcam=R∗Pworld+T
其中 P c a m Pcam Pcam表示相机坐标系下的目标点坐标, R R R为选择矩阵, T T T为平移向量, P w o r l d Pworld Pworld为世界坐标系下的目标点坐标
相机坐标系的 P c a m Pcam Pcam点的 Z Z Z轴长度 Z c Zc Zc就是距离信息,即:
Z c = X w ∗ R 31 + Y w ∗ R 32 + Z w ∗ R 33 + T 3 Zc=Xw*R31+Yw*R32+Zw*R33+T3 Zc=Xw∗R31+Yw∗R32+Zw∗R33+T3
基于世界平面坐标的前提,简化为:
Z c = X w ∗ R 31 + Y w ∗ R 32 + T 3 Zc=Xw*R31+Yw*R32+T3 Zc=Xw∗R31+Yw∗R32+T3
根据 图像坐标与世界平面坐标的关系式 计算得到的世界平面坐标点 ( X w , Y W ) (Xw, YW) (Xw,YW)代入简化式即可求出 Z c Zc Zc距离信息
法二:根据焦距和世界坐标点计算距离
d i s t a n c e = F c ∗ W / ′ w distance = Fc * W / 'w distance=Fc∗W/′w
其中 d i s t a n c e distance distance表示测量目标与相机的距离, F c Fc Fc表示焦距, W W W表示世界坐标系下的目标宽度, ′ w 'w ′w表示图像坐标系下的目标宽度
图像坐标系的目标宽度 ′ w 'w ′w 可由 像素坐标(u, v)与图像坐标(x, y)的关系式基于两个像素坐标点(u1, v1)和(u2, v2)计算得到两个图像坐标系下的坐标点(x1, y1)和(x2, y2),再通过欧式距离计算得到 ′ w 'w ′w;
世界坐标系的目标宽度 W W W 可由 图像坐标与世界平面坐标的关系式 基于两个图像坐标点(x1, y1)和(x2, y2)计算得到两个世界平面坐标系下的坐标点(Xw1, Yw1)和(Xw2,Yx2),再通过欧式距离计算得到 W W W;