自动驾驶之—2D到3D升维

前言：
最近在学习自动驾驶方向的东西，简单整理一些学习笔记，学习过程中发现宝藏up 手写AI

1. 3D卷积

3D卷积的作用：对于2DCNN，我们知道可以很好的处理单张图片中的信息，但是其对于视频这种由多帧图像组成的图片流，以及CT****等一些医学上的3维图像就会显得束手无策。因为2D卷积没有考虑到图像之间时间维度上的物体运动信息的变化（3维CT图像也可以近似看为是二维图像在时间上的变化）。因此，为了能够对视频（包括3维医学图像）信息进行特征提取，以便用来分类及分割任务，提出了3D卷积，在卷积核中加入时间维度。

1. pytorch中对应函数介绍

class torch.nn.Conv3d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
说明：
参数kernel_size，stride，padding，dilation可以是一个int的数据 - 卷积height和width值相同，也可以是一个有三个int数据的tuple数组，tuple的第一维度表示depth的数值，tuple的第二维度表示height的数值，tuple的第三维度表示width的数值
Parameters：
in_channels(int) – 输入的通道数
out_channels(int) – 输出的通道数
kernel_size(int or tuple) - 卷积核的尺寸
stride(int or tuple, optional) - 卷积步长
padding(int or tuple, optional) - 边缘填充的像素个数
dilation(int or tuple, optional) – 卷积核元素之间的间距
groups(int, optional) – 卷积的组数
bias(bool, optional) - 如果bias=True，添加偏置

举个栗子：

# With square kernels and equal stride
m = nn.Conv3d(16, 33, 3, stride=2)
# non-square kernels and unequal stride and with padding
m = nn.Conv3d(16, 33, (3, 5, 2), stride=(2, 1, 1), padding=(4, 2, 0))
input = autograd.Variable(torch.randn(20, 16, 10, 50, 100))
output = m(input)

1. 3D卷积图示：

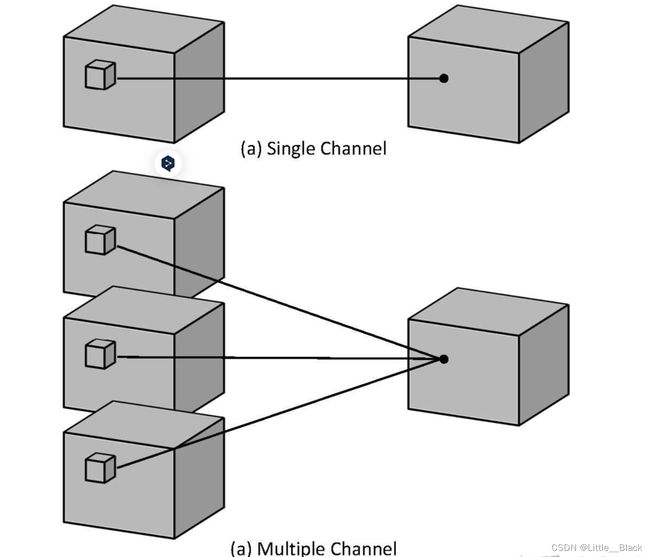
针对单通道，与2D卷积不同之处在于，输入图像多了一个 depth 维度，故输入大小为(1, depth, height, width)，卷积核也多了一个k_d维度，因此卷积核在输入3D图像的空间维度（height和width维）和depth维度上均进行滑窗操作，每次滑窗与 (k_d, k_h, k_w) 窗口内的values进行相关操作，得到输出3D图像中的一个value.

针对多通道，输入大小为(3, depth, height, width)，则与2D卷积的操作一样，每次滑窗与3个channels上的 (k_d, k_h, k_w) 窗口内的所有values进行相关操作，得到输出3D图像中的一个value。

1. 立体视觉

2.1 原理简介

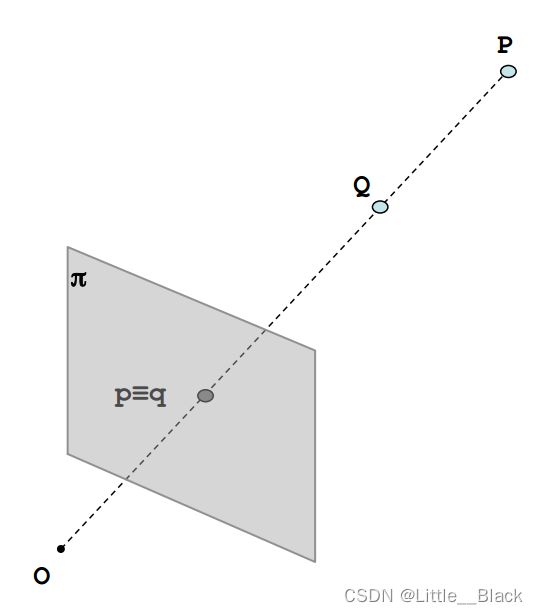
使用两个或多个从不同角度拍摄的2D图像来估计每个像素的深度，从而重建3D场景。.一般而言，立体视觉系统需要有两个（或者两个以上）摄像头的支持，也就正如人类的双眼一样。

2.2 单目视觉

O点为相机的光心，π是摄像头的成像平面。

从图中可以看出，如果P点与Q点在同一条直线上，那么他们在图像上的成像点就是同一个点，也就是$p\equiv q$ ，那么也就看不出来他们在距离上的差异（也就无法知道Q在前还是P在前）。

2.3 双目视觉

正是在发现了单目系统的缺陷之后，我们将系统由一个摄像头增加到两个摄像头，这样也就构成了一个立体系统。如果我们可以在两幅图像中找到对应点，我们就可以通过三角测量的方法来求得深度

从图中可以很明显的看出，在增加了一个摄像头之后，P与Q在目标面T上的成像不在位于同一个点，而是有自己分别的成像点，也就是$q^{{}^{\prime }}$ 与 $p^{{}^{\prime }}$。

那么，在我们给出了Reference与Target之后，我们应该如何解决参考面与目标面之间的对应关系呢？

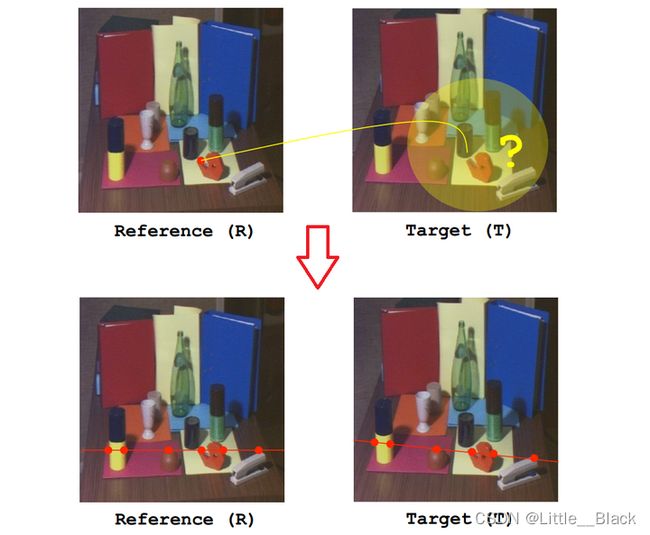
这个时候，就需要对极约束（极线约束），对极约束意味着一旦我们知道了立体视觉系统的对极几何之后，对两幅图像间匹配特征的二维搜索就转变成了沿着极线的一维搜索。

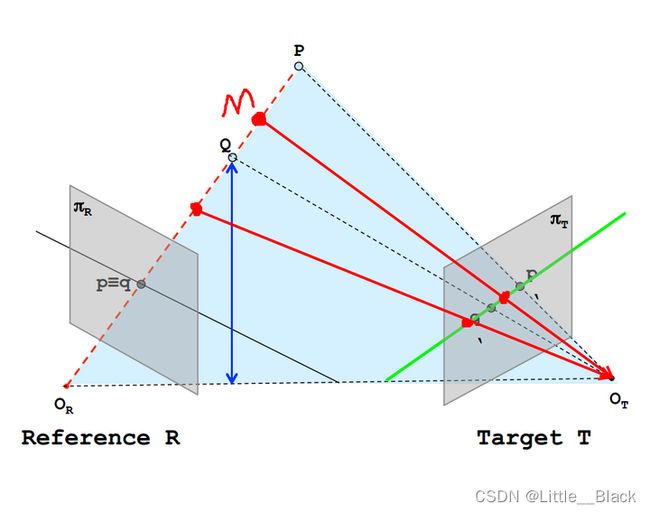
图中黑色实线为R平面一条极线，绿色为T平面一条极线。给定一幅图像上的一个特征，它在另一幅图像上的匹配视图一定在对应的极线上（图中将P，Q视为特征，可以看到在T上的成像在绿色直线上）

通常我们使用的立体视觉系统都是比较标准的系统，如图所示：

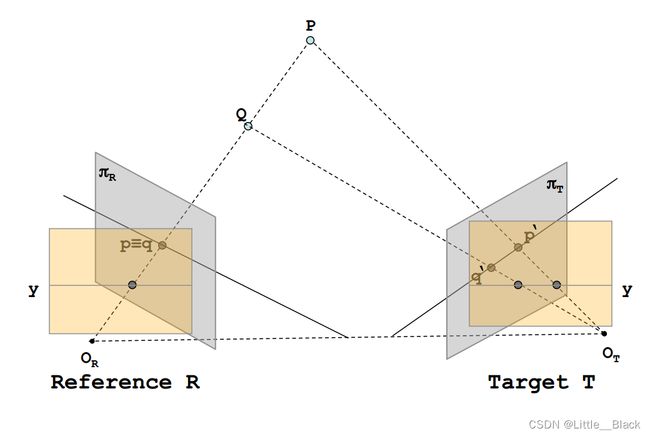
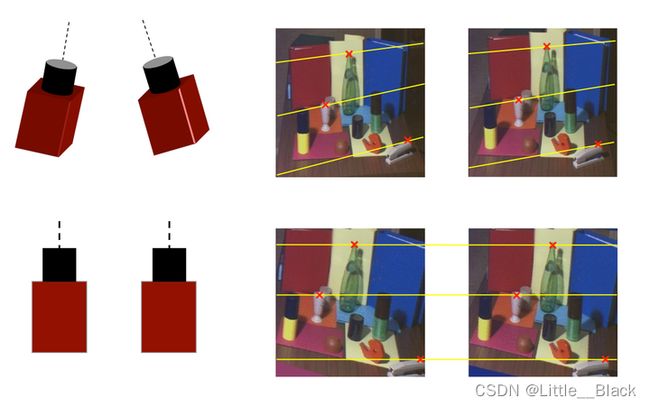
一旦我们知道了对应点的搜索区域，就可以将其从2D降到1D，这样就形成了更加方便的立体视觉，对应点都被约束再同一条极线上，也就是图中的y直线。下面给出一个实际的示例（在理想情况下，我们希望两个摄像头的参数是完全一致的，并且两个相机的位置是平行的）。

2.4 视差和深度计算原理

在我们已经确保两个摄像头的参数是完全一致的，并且两者的位置是平行之后，我们的关注点就落到了如何计算物体的深度信息，这也是最重要最关键的地方。下面给出的是标准立体视觉系统下的计算原理。

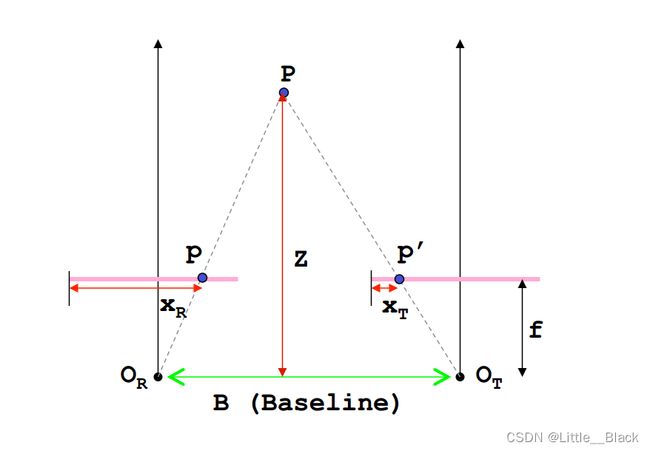
假设 $P$ 为空间中的一点，$O_R$为左边摄像头的光心，$O_T$为右边摄像头的光心，摄像头的焦距为$f$(光心到成像平面的距离)，成像平面在图中用粉色线表示，$B$表示两个摄像头光心之间的距离，也称为基线，$P$在左右两个摄像机成像平面上的成像点分别为$p$与$p^{\prime }$，$x_R$与$x_T$为成像点的水平方向距离(通常我们得到的是像素坐标系下的$x$左边，其单位为像素，因此需要转换为实际的物理长度，涉及到坐标系转换问题)，$Z$就是我们需要求的深度。

根据三角形相似定理($\Delta Pp{p}^{\prime }$~ $\Delta P{O}_R{O}_T$):

$\frac{B}{Z}=\frac{B-(x_R-x_T)}{Z-f}$===> $Z=\frac{B\cdot f}{x_R-x_T}=\frac{B\cdot f}{D}$

其中 $D=x_R-x_T$ 就是我们通常所说的视差(disparity)。

我们可以发现，深度Z是跟视差D成反比关系的，当视差D越小时，Z越大，物体离立体视觉系统也就越远， 当视差D越大，Z越小，物体离立体视觉系统也就越近。这一点和我们人眼系统是一样的，当我们观察离我们比较近的物体的时候，视差很大，可以获得的信息也就越多，当物体离我们很远的时候，视差很小，我们获得的信息也就很少了。

在图像处理中，我们通常用灰度值来表示视差信息，视差越大，其灰度值也就越大，在视差图像的视觉效果上表现出来就是图像越亮，物体离我们越远，其视差越小，灰度值也越小，视差图像也就越暗。

2.5 深度估计

• 工作原理：使用深度学习模型来预测2D图像中每个像素的深度
• 优势：可以从单个2D图像中获得3D深度信息
• 应用：增强现实、虚拟现实、3D重建

1. 3D到2D下采样

3.1

世界坐标系 —> 相机坐标系 —> 投影矩阵 —> 像素映射 —> 生成图片

• 世界坐标系和相机坐标系转换可以通过dcm矩阵计算求出：

def dcm(origin: np.ndarray, target: np.ndarray):
    """
    3 * 3 矩阵 ，{x,y,z}T 将origin坐标系转换到target坐标系的dcm旋转矩阵
    Args:
        origin:
        target:
    Returns:
    """
    matrix = np.zeros((3, 3))
    for i in range(3):
        for j in range(3):
            matrix[i, j] = np.dot(target[i], origin[j])
    return matrix.T

• 投影矩阵，可以参考pyrender.camera.py中的透视投影和正交投影矩阵，也可以根据自己的需求定制
• 通过前两步计算出2d投影点，会落在(-1, 1)范围内，通过像素映射完成3d点到2d点的投影

完整代码：

class Camera:
    def __init__(self, scale, translation, resolution, znear=0.05, zfar=1000):
        self.scale = np.array(scale)  # 相机缩放
        self.translation = np.array(translation)  # 相机位移
        self.resolution = np.array(resolution)  # 2d 分辨率
        self.znear = znear  # 近平面
        self.h_s = self.resolution / 2  # h/2 w/2
        self.center = self.h_s  # 2d投影面中心点

    def camera_matrix(self):
        """
        相机外参矩阵，世界坐标系转相机坐标系
        Returns:
        """
        world = np.eye(3)
        camera = np.eye(3)
        camera[-1, -1] = -1
        matrix = np.eye(4)
        matrix[:3, :3] = dcm(world, camera)
        return matrix

    def get_projection_matrix(self) -> np.ndarray:
        """
        投影矩阵 业务定制
        Returns:
        """
        P = np.eye(4)
        P[0, 0] = self.scale[0]
        P[1, 1] = self.scale[1]
        P[0, 3] = self.translation[0] * self.scale[0]
        P[1, 3] = -self.translation[1] * self.scale[1]
        P[2, 2] = -1
        return P


class Render:
    def __init__(self, camera: Camera):
        self.camera = camera

    def p_point(self, point: np.ndarray):
        """
        投影点坐标
        Args:
            point: 点 4D 例如[0.5,0.5,0.5,1]  3d点需要填充1
        Returns:
        """
        p = self.camera.get_projection_matrix().dot(self.camera.camera_matrix().dot(point)) 
        p = p[:2] / p[-1] * self.camera.h_s * np.array([1, -1]) + self.camera.center
        return p

3.2 2.5D表示：

2D、2.5D和3D是描述物体和场景在空间中表示的三种方式，2D(平面)与3D(立体)又称为二维和三维，他们之间的区别是：2D你只能看到一个面，3D你能看到所有的面。

• 定义：
  • 2D(二维)：在2D中，物体或场景只有长度和宽度两个维度，常见的2D表示有图片、图画和屏幕上的图像
  • 2.5D(二点五维)：介于2D和3D之间，它通常描述的是一个场景从特定角度的深度信息，一个2.5D图像（例如深度图）为每个像素提供了一个深度值。
  • 3D(三维)：3D表示考虑了长度、宽度和深度，它为场景中的每个点提供了完整的三维坐标，常见的3D表示包括3D模型、点云等。
• 区别：
  • 维度和信息完整性：2D缺乏深度信息；2.5D提供了从某个视角的深度信息；3D提供了完整的三维坐标信息。
  • 视角依赖性：2.5D通常与特定的视角相关，而3D表示是视角无关的
  • 数据复杂性：2D数据最简单，只需要x和y坐标；2.5D需要x、y和深度；3D需要x、y和z三个坐标。
• 联系：
  • 从2D到2.5D: 如果你有一个2D图像和与之相关的深度信息，你可以得到一个2.5D表示。例如，使用深度相机如Kinect可以得到深度图。
  • 从2D到3D: 通过多个2D图像和某种形式的结构从运动或立体视觉，你可以重建出3D场景或物体。但这比从2.5D到3D更为复杂。
  • 从2.5D到3D: 从深度图中可以重建3D信息，例如生成一个点云。但由于2.5D信息通常是从一个视角获得的，因此可能不能完全恢复物体或场景的所有3D信息。
  • 简而言之，2D、2.5D和3D代表了逐渐增加的空间信息和复杂性。2.5D是一个中间表示，提供了比2D更多的深度信息，但没有3D那么完整。
• 2D与2.5D的关系可以看成X轴与Y轴旋转了指定的角度后形成的新的屏幕

  • 坐标旋转算法：

  • 

  • 根据三角函数公式：

  • $\sin (A+B)=\sin A\ast \cos B+\sin B\ast \cos A$

  • $\cos (A+B)=\cos A\ast \cos B-\sin A\ast \sin B$

  • 线段由$BO$转到$AO$,旋转后的坐标计算公式如下：

  • $(x,y)\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right]=(x\ast cos\theta -y\ast sin\theta ,x\ast sin\theta +y\ast cos\theta )$

通过矩阵的知识可以知道，X轴的基向量为[1,0]；Y轴的基向量为[0,1]。有X和Y轴基向量组成的矩阵是一个单位矩阵。所以常规的平面直角坐标系的任何一点可以表示为：

$$(x,y)\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=(x1,y1)$$

为了将2D坐标映射到2.5D坐标，需要定义2.5D坐标系统使用的基向量。因为2.5D坐标系实际上是通过旋转X与Y轴实现的，所以通过旋转算法和上面的单位矩阵，可以得到新坐标系的X和Y轴基向量：

$$\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\alpha & cos\alpha \end{array}\right]=\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\alpha & cos\alpha \end{array}\right]$$

可以看出，将2D坐标系中的基向量转换为2.5D坐标系统的基向量时，结果其实就是旋转矩阵本身，这个旋转矩阵就是2.5D坐标系中的X和Y轴基向量。

注意：这里分别使用θ和α，是因为X和Y轴可以旋转不同的角度。如果 θ+α=90度，那么Sin(α)=Cos( θ )；Cos(α)=Sin( θ )。上面的矩阵可以被替换为：

$$\left[\begin{array}{cc}cos\theta & sin\theta \\ -cos\theta & sin\theta \end{array}\right]$$

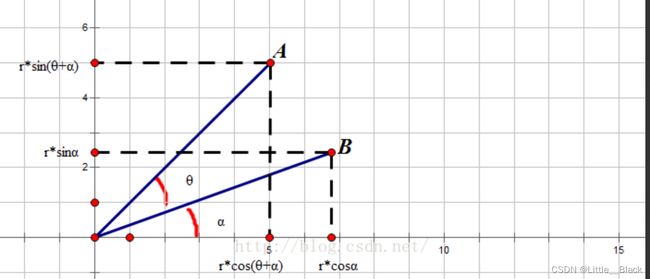
现在定义2D坐标系为W(x,y)，2.5D坐标系为G(x,y)。2D坐标系的X轴相对于2.5D坐标系X轴顺时针旋转30°，Y轴旋转60°。通过上面的公式可以得到W(x,y)对应的G(x,y)：

$G_x=(W_x-W_y)\ast cos\theta$

$G_y=(W_x+W_y)\ast sin\theta$

2.5D坐标只需利用上面的工作进行逆运算就能得到：

$$W_x=(G_x\ast sin\theta +G_y\ast cos\theta )/2\ast sin\theta \ast cos\theta$$

$$W_y=(G_y\ast cos\theta -G_x\ast sin\theta )/2\ast sin\theta \ast cos\theta$$

1. 混合方法

4.1 多视图网络

• 工作原理：使用从不同角度的多个2D视图的信息来提取3D特征。
• 应用：3D物体识别、3D重建。
• 优点：能够从不同的2D视图中捕获3D信息。

4.2 融合2D和3D特征

• 工作原理：将2D图像特征与3D数据特征（例如点云）结合起来。
• 应用：3D物体检测、场景分割。
• 优点：利用了2D图像和3D结构的强大信息。