【数据结构与算法】二叉树的知识讲解
目录
一,二叉树的结构深入认识
二,二叉树的遍历
三,二叉树的基本运算
3-1,计算二叉树的大小
3-2,统计二叉树叶子结点个数
3-3,计算第k层的节点个数
3-4,查找指定值的结点
一,二叉树的结构深入认识
二叉树是不可随机访问的,二叉树的结构是通过双亲结点与孩子结点之间的连接进行遍历访问,因此,二叉树的结构是用链式结构来存储的。如下:
二叉树的结构
#include
#include
typedef struct Tree {
int val;//数据
struct Tree* leftchild;//左孩子结点
struct Tree* rightchild;//右孩子结点
}Tree;
要说明的是,学习二叉树的结构不跟栈和队列之类的一样用于增删查改,二叉树没有这些操作,二叉树的运用比较复杂,下面会依次讲解。
二,二叉树的遍历
二叉树的遍历有:前序遍历,中序遍历,后序遍历,层序。通常,在这些遍历算法中除了层序遍历外,其它的遍历都要运用递归结构。
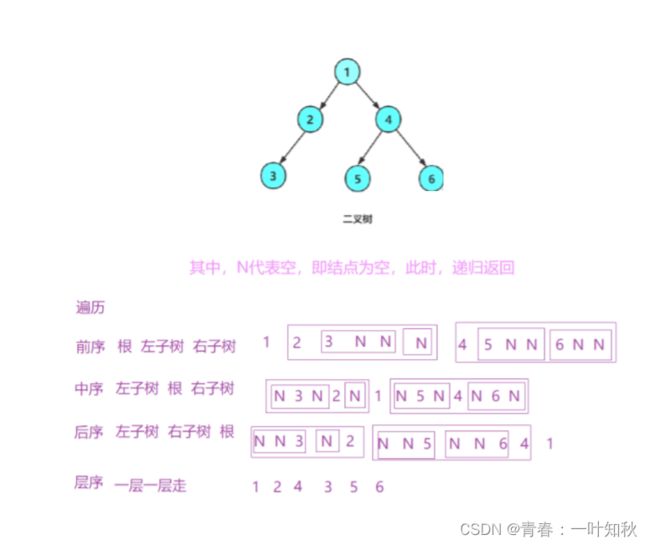
1,前序遍历(也称先序遍历)——访问根结点的操作发生在遍历其左右子树之前,即遍历的
顺序为:根,左子树,右子树。
2,中序遍历——访问根结点的操作发生在遍历其左右子树之间。即遍历的顺序为:左子树,根,右子树。
3,后序遍历——访问根结点的操作发生在遍历其左右子树之后。即遍历的顺序为:左子树,右子树,根。
4,层序遍历——从左到右一层一层的遍历,此遍历非常简单,就如从开始到结尾的遍历顺序表一样。
注意:这里要说明的是,以上的遍历除了层序遍历外,其它的遍历都是递归式的遍历,可不是单纯普通式按照以上顺序循环式的遍历,正确的遍历如下图:
说明一下,在二叉树的遍历中,前,中,后遍历的思路基本相同,而层序遍历一般要借助队的结构来实现,本篇文章先不做介绍,后文深入运用时会详细说明。前中后的三种遍历代码如下:
//前序遍历
void FrontOrder(struct Tree* root) {
//当递归到空结点时退出
if (root == NULL) {
return;
}
//输出
fprintf(stdout, "%d ", root->val);
//递归左子树
FrontOrder(root->leftchild);
//递归右子树
FrontOrder(root->rightchild);
}
//中序遍历
void MiddleOrder(struct Tree* root) {
//当递归到空结点时退出
if (root == NULL) {
return;
}
//递归左子树
MiddleOrder(root->leftchild);
//输出
fprintf(stdout, "%d ", root->val);
//递归右子树
MiddleOrder(root->rightchild);
}
//后序遍历
void RearOrder(struct Tree* root) {
//当递归到空结点时退出
if (root == NULL) {
return;
}
//递归左子树
RearOrder(root->val);
//递归右子树
RearOrder(root->val);
//输出
fprintf(stdout, "%d ", root->val);
}
解析:
递归本身有点不好理解,而上面的递归遍历中,当进行递归遍历时,可看做从此函数的根结点开始不断往下面的左右孩子结点遍历,当递归到根结点为空时结束下一次递归,并返回到此结点的双亲结点,可以说二叉树的递归遍历是不断往下层进行的,只有当遍历到最下层或下层的空结点时才返回,也就是递归遍历是从最后开始,然后不断往回返,直到返回到二叉结构的根节点才结束整个递归程序。
补充:
函数的递归其实跟我们学习的栈结构一样,递归入函数(即进入函数栈帧)相当于入栈,出函数(即函数栈帧的销毁)相当于出栈。
学习建议:
遍历思想是学习二叉树的基本,很多二叉树的算法思想都要在此递归遍历的思想上进行开阔的,因此,如果这中递归思路不明白,一定要先理清思路,不建议先往后面看。
三,二叉树的基本运算
在讲解这一部分内容前,我们要先明白递归中设置局部变量的用法。
二叉树递归设置局部变量的注意:
在二叉树计数中,我们难免要设定局部变量,而在进行递归返回中可能有些人说函数的返回值会覆盖之前的值,不明白为什么覆盖后的值就是我们想要统计的数值。其实这原理很简单,在讲解二叉树遍历的解析说过,二叉树的递归遍历是不断往下层进行的,只有当遍历到最下层时才返回,也就是递归程序是从最后开始,不断往前返回,当我们递归遍历二叉树时,满足计数的条件会不断往上层返,这时计数的值相当于以此函数中root为根结点的子树的以下计数值,也就是我们要统计的数值。
3-1,计算二叉树的大小
计算二叉树的大小说白了就是确定有几个不为空的结点,此算法比较简单,我们可直接遍历整个二叉结构不断加一来实现。代码如下:
//统计二叉树中叶子结点的个数
int TreeSize(Tree* root) {
//当为空结点时说明此时为0
if (root == NULL) {
return 0;
}
//不断递归遍历,遍历一个结点加1。
return TreeSize(root->leftchild) + TreeSize(root->rightchild) + 1;
}以上代码虽然省力,但可能对于部分人来说比较难理解,展开后的代码如下:
int TreeSize(Tree* root) {
if (root == NULL) {
return 0;
}
//遍历左子树的结点个数
int leftsize = TreeSize(root->leftchild);
//遍历右子树的结点个数
int rightsize = TreeSize(root->rightchild);
//返回以此结点为根结点的二叉树结点个数,此二叉树是子二叉树
return leftsize + rightsize + 1;
}对于当初学者笔者建议用展开后的代码,对递归了解比较深入后再用合成版代码。
3-2,统计二叉树叶子结点个数
此算法与计算二叉树的结点个数方法相似,不同的是,当进行递归遍历时,我们可利用叶子结点的左右孩子都为空的特点来计数,当递归遍历时满足这一特点进行计数,不满足进行递归遍历,代码如下:
int LeavesNodeSize(Tree* root) {
if (root == NULL) {
return 0;
}
//当此结点是叶子结点时,计数1
if (root->leftchild == NULL && root->rightchild == NULL) {
return 1;
}
//左孩子结点的叶子结点数
int count1 = LeavesNodeSize(root->leftchild);
//右孩子结点的叶子结点数
int count2 = LeavesNodeSize(root->rightchild);
//返回当前以root为根结点的子二叉树的叶子结点总个数
return count1 + count2;
}当我们明白以上原理后可进行简化算法,跟之前一样,先理清以上思路再进行简化。如下:
int LeavesNodeSize(Tree* root) {
if (root == NULL) {
return 0;
}
if (root->leftchild == NULL && root->rightchild == NULL) {
return 1;
}
return LeavesNodeSize(root->leftchild) + LeavesNodeSize(root->rightchild);
}3-3,计算第k层的节点个数
记录第k层的二叉树结点也是同理,在递归遍历过程中,往下层递归一次将k减1,当k==1时就递归到了第k层,也就是在此时开始计数,而函数返回值将返回以此函数中的root为根结点的子二叉树的第k层结点数。
int NodeCount(Tree* root, int k) {
if (root == NULL) {
return 0;
}
//当k == 1 时此时遍历到了第k层,此时计数
if (k == 1) {
return 1;
}
//以此函数的root为根结点以下的子二叉树第k层的左孩子结点数
int leftchild = NodeCount(root->leftchild, k - 1);
//以此函数的root为根结点以下的子二叉树第k层的右孩子结点数
int rightchild = NodeCount(root->rightchild, k - 1);
//返回以此函数的root为根结点以下的子二叉树第k层的结点数
return leftchild + rightchild;
}算法合并简化后如下:
int NodeCount(Tree* root, int k) {
if (root == NULL) {
return 0;
}
if (k == 1) {
return 1;
}
return NodeCount(root->leftchild, k - 1) + NodeCount(root->rightchild, k - 1);
}3-4,查找指定值的结点
此算法的坑比较多,首先我们要考虑的是当遍历到要查找的结点时如何停止遍历,并最终返回该结点。要知道一点,当我们要查找的结点在中间时,直接返回是上一次的递归函数,因此,我们要做的是让查找的指定结点不断返回,直到递归结束。
算法详细步骤如下:
Tree* FoundNode(Tree* root, int x) {
if (root == NULL) {
return NULL;
}
if (root->val == x) {
return root;
}
Tree* leftchild = FoundNode(root->leftchild, x);
//当左孩子是我们要找的结点时就不往下继续遍历了,直接返回此结点
if (leftchild != NULL && leftchild->val == x) {
return leftchild;
}
Tree* rightchild = FoundNode(root->rightchild, x);
//当左孩子是我们要找的结点时就不往下继续遍历了,直接返回此结点
if (rightchild != NULL && rightchild->val == x) {
return rightchild;
}
//当查找不到返回NULL
return NULL;
}算法的化简代码如下:
Tree* FoundNode(Tree* root, int x) {
if (root == NULL) {
return NULL;
}
if (root->val == x) {
return root;
}
Tree* leftchild = FoundNode(root->leftchild, x);
//当左孩子是我们要找的结点时就不往下继续遍历了,直接返回此结点
if (leftchild != NULL && leftchild->val == x) {
return leftchild;
}
//遍历右结点,当右孩子是我们要找的结点时返回此结点
return FoundNode(root->rightchild, x);
}总结:学习到这里学者们明显感到难度增大了,不过也不用担心,只要我们多多思考并加之练习,其实逻辑也不是那么难,上面的算法程序笔者之所以将步骤展开和步骤合并一并写入,就是为了让大家多多练习以上的思路,其实逻辑也都是一样的,只是为了强化思维罢了。