数据结构和算法（14）：串

串及串匹配

串或字符串（string）属于线性结构，可直接利用向量或列表等序列结构加以实现：结构简单，规模庞大，元素重复率高。

串

由 n 个字符构成的串记作：$S="a_0{a}_1...a_{n-1}"$ 其中，$a_i\in \sum ,0\le i<n$ 其中 $\sum$ 是所有可用字符的集合，称作字符表。

字符串中任一连续的片段，称作其子串。
两种特殊子串：
1.起始于位置0、长度为k的子串称为前缀；
2.终止于位置n - 1、长度为k的子串称为后缀；
空串是任何字符串的子串，也是任何字符串的前缀和后缀；任何字符串都是自己的子串，也是自己的前缀和后缀。
此类子串、前缀和后缀分别称作平凡子串、平凡前缀和平凡后缀。
反之，字符串本身之外的所有非空子串、前缀和后缀，分别称作真子串、真前缀和真后缀。

判等： 字符串S[0, n)和T[0, m)称作相等，当且仅当二者长度相等（n = m），且对应的字符分别相同（对任何 $0\le i<n$ 都有 $S[i]=T[i]$）.

串匹配

如何在字符串数据中，检测和提取以字符串形式给出的某一局部特征？这类操作都属于串模式匹配范畴，简称串匹配

对基于同一字符表的任何文本串 T (|T| = n ) 和 模式串P(|P| = m)：
1.判定T 中是否存在某一子串与P相同；
2.若存在（匹配）， 则报告该子串在T中的起始位置。

蛮力算法

将P与T中长度为m的n - m + 1个子串逐一比对，即可确定可能的匹配位置。

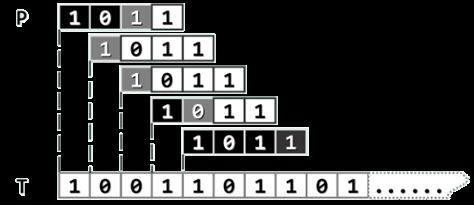
正确性： 只有在某一轮的m次比对全部成功之后才成功返回，故不致于误报；反过来，所有对齐位置都会逐一尝试，故亦不致漏报。

实现1

int match ( char* P,char* T ) { //串匹配算法( Brute-force-1 )
	size_t n = strlen( T ), i = 0;	//文本串长度、当前接受比对字符的位置
	size_t m = strlen( P ), j = 0;	//模式串长度、当前接受比对字符的位置
	while ( j < m && i <n )	//自左向右逐个比对字符
		if ( T[i] == P[j] )	//若匹配
		{ i ++; j ++; }	//则转到下一对字符
		else //否则
		{ i -= j - 1; j= 0; }	//文本串回退、模式串复位
	return i - j;	//如何通过返回值，判断匹配结果?
}

借助整数i和j，分别指示T和P中当前接受比对的字符T[i]与P[j]。若当前字符对匹配，则i和j同时递增以指向下一对字符。一旦j增长到m则意味着发现了匹配，即可返回P相对于T的对齐位置i - j。一旦当前字符对失配，则i回退并指向T中当前对齐位置的下一字符，同时j复位至P的首字符处，然后开始下一轮比对。

实现2

int match ( char* P, char* T ) { //串匹配算法( Brute-force-2 )
	size_t n = strlen ( T ), i = 0;	//文本串长度、与模式串首字符的对齐位置
	size_t m = strlen ( P ), j;	//模式串长度、当前接受比对字符的位置
	for ( i = 0; i <n - m + 1; i++ ) {	//文本串从第i个字符起，与
		for ( j = 0; j <m; j++ )	//模式串中对应的字符逐个比对
			if ( T[i + j] != P[j] ) break;//若失配，模式串整体右移一个字符，再做一轮比对
		if ( j >= m ) break;//找到匹配子串
	}
	return i; //如何通过返回值，判断匹配结果?
}

借助整数i指示P相对于T的对齐位置，且随着i不断递增，对齐的位置逐步右移。在每一对齐位置i处，另一整数j从0递增至m - 1，依次指示当前接受比对的字符为T[i + j]与P[j]。因此，一旦发现匹配，即可直接返回当前的对齐位置i。

复杂度

从理论上讲，蛮力算法至多迭代 n - m + 1 轮，且各轮至多需进行 m 次比对，故总共只需做不超过 (n - m + 1)∙m 次比对。
因 m << n，渐进的时间复杂度应为O(n∙m)。最好为O(n)。

KMP 算法

蛮力算法在最坏情况下所需时间，为文本串长度与模式串长度的乘积。
问题在于这里存在大量的局部匹配：每一轮的m次比对中，仅最后一次可能失配。而一旦发现失配，文本串、模式串的字符指针都要回退，并从头开始下一轮尝试。

蛮力算法会令两个字符指针同步回退（即令i = i - j + 1和j = 0），然后再从这一位置继续比对。

记忆法

用T[i]和P[j]分别表示当前正在接受比对的一对字符。

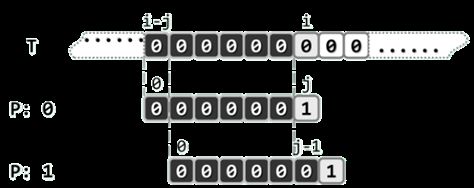
利用以往的成功比对所提供的信息（记忆），不仅可避免文本串字符指针的回退，而且可使模式串尽可能大跨度地右移（经验）。
子串T[i - j, i)完全由0组成，在回退之后紧接着的下一轮比对中，前j - 1次比对必然都会成功。因此，可直接令i保持不变，令j = j - 1，然后继续比对。如此，下一轮只需1次比对，共减少j - 1次。即令P相对于T右移一个单元，然后从前一失配位置继续比对。

查询表

假设前一轮比对终止于T[i] ！= P[j]，指针i不必回退，而是将T[i]与P[t]对齐并开始下一轮比对。那么，t准确地应该取作多少？

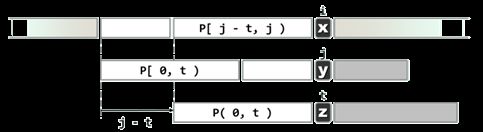
经过此前一轮的比对，已经确定匹配的范围应为：P[0, j) = T[i - j, i)
若模式串P经适当右移之后，能够与T的某一（包含T[i]在内的）子串完全匹配，则一项必要条件就是：P[0, t) = T[i - t, i) = P[j - t, j)

在P[0, j)中长度为t的真前缀，应与长度为t的真后缀完全匹配，故t必来自集合：$N(P,j)=\{0\le t<j|P[0,t)=P[j-t,j)\}$

若下一轮比对将从T[i]与P[t]的比对开始，这等效于将P右移j - t个单元，位移量与t成反比。因此，为保证P与T的对齐位置（指针i）绝不倒退，同时又不致遗漏任何可能的匹配，应在集合N(P, j)中挑选最大的t。也就是说，当有多个值得试探的右移方案时，应该保守地选择其中移动距离最短者。

若令：next[j] = max(N(P, j))，则一旦发现P[j]与T[i]失配，即可转而将P[next[j]]与T[i]彼此对准，并从这一位置开始继续下一轮比对。
对于任一模式串P，不妨通过预处理提前计算出所有位置j所对应的next[j]值，并整理为表格以便此后反复查询——亦即，将“记忆力”转化为“预知力”

实现

int match ( char* P, char* T ) {	//KMP算法
	int* next = buildNext ( P );	//构造next表
	int n = ( int ) strlen ( T ), i = 0;	//文本串指针
	int m = ( int ) strlen ( P )， j = 0;	//模式串指针
	while ( j <m && i <n ) //自左向右逐个比对字符
		if ( 0 > j || T[i] == P[j])	//若匹配，或P已移出最左侧（两个判断的次序不可交换)
			{ i ++; j ++;}	//则转到下一字符
		else //否则
			j = next[j];	//模式串右移（注意∶文本串不用回退)
	delete [] next;	//释放next表
	return i - j;
}

理解 next[ ] 表

next[ 0 ] = -1

只要 $j>0$ 则必有 $0\in N(P,j)$。此时 $N(P,j)$ 非空，从而可以保证“在其中取最大值”这一操作的确可行。

若在某一轮比对中首对字符即失配，则应将P直接右移一个字符，然后启动下一轮比对。

假想地在P[0]的左侧“附加”一个P[-1]，且该字符与任何字符都是匹配的。
就实际效果而言，这一处理方法完全等同于“令next[0] = -1”

next[ j + 1]

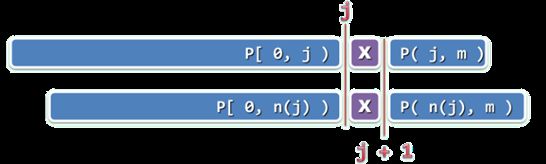
若next[j] = t，则意味着在P[0, j)中，自匹配的真前缀和真后缀的最大长度为t，故必有 next[j + 1] <= next[j] + 1；
P[j] = P[ next[j] ]时，必有 next[j + 1] = next[j] + 1

若next[j] ！= t，next[j + 1]的下一候选者应该依次是next[ next[j] ] + 1, next[ next[ next[j] ] ] + 1, …

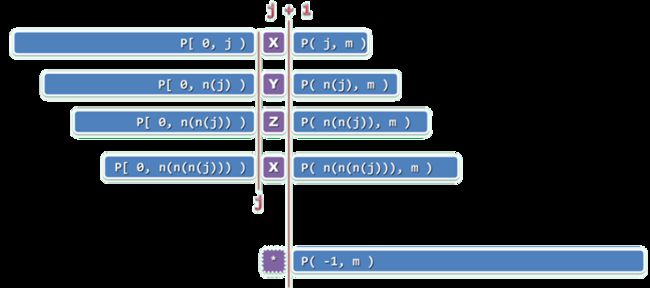
反复用next[t]替换t（即令t = next[t]），即可按优先次序遍历以上候选者；一旦发现P[j]与P[t]匹配（含与P[t = -1]的通配），即可令next[j + 1] = next[t] + 1。

总有next[t] < t，在此过程中t必然严格递减；同时，即便t降低至0，亦必然会终止于通配的next[0] = -1，而不致下溢。

构造 next[ ] 表

int* buildNext ( char* P ) {	//构造模式串P的next表
	size_t m = strlen ( P )， j = 0; 	//“主”串指针
	int* N = new int[m]; //next表
	int t = N[0] = -1;	//模式串指针
	while ( j < m - 1 )
		if ( 0 > t || P[j] == P[t] ) {	//匹配
			j ++; t ++;
			N[j] = t; //此句可改进...
		}else //失配
			t = N[t];
	return N;
}

分摊分析

纵观算法的整个过程：启动时有i = j = 0，即k = 0；算法结束时i <= n且j >=0，故有k<= 2n。在此期间尽管整数k从0开始持续地严格递增，但累计增幅不超过2n，故while循环至多执行2n轮。另外，while循环体内部不含任何循环或调用，故只需O(1)时间。因此，若不计构造next表所需的时间，KMP算法本身的运行时间不超过O(n)。

也就是说，尽管可能有O(n)个对齐位置，但就分摊意义而言，在每一对齐位置仅需O(1)次比对。
既然next表构造算法的流程与KMP算法并无实质区别，故仿照上述分析可知，next表的构造仅需O(m)时间。综上可知，KMP算法的总体运行时间为O(n + m)。

改进

按照此前定义的next表，仍有可能进行多次本不必要的字符比对操作。

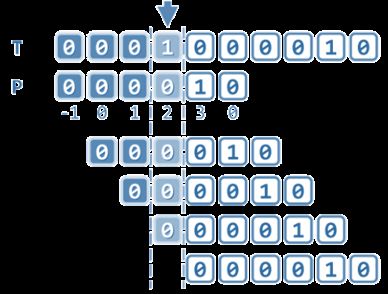
经过此前的比对已发现 T[i] != P[3]，那么继续将T[i]和那些与P[3]相同的字符做比对，既重蹈覆辙，更徒劳无益。

集合N(P, j)的定义修改为：N(P, j) = { 0 <= t < j | P[0, t) = P[j - t, j) 且 P[t] != P[j] }。
也就是说，除“对应于自匹配长度”以外，t只有还同时满足“当前字符对不匹配”的必要条件，方能归入集合N(P, j)并作为next表项的候选。

int* buildNext ( char* P ) {	//构造模式串P的next表（改进版本)
	size_t m = strlen ( P ),j = 0; 	//“主”串指针
	int* N = new int[m]; 			//next表
	int t = N[0] = -1;				//模式串指针
	while ( j < m - 1 )
		if ( 0 > t ll P[j] == P[t] ) { 	//匹配
		j ++; t ++;
		N[j] = (P[j] != P[t] ? t : N[t] );	//注意此句与未改进之前的区别
	} else //失配
		t = N[t];
		return N;
}

改进后的算法与原算法的唯一区别在于，每次在P[0, j)中发现长度为t的真前缀和真后缀相互匹配之后，还需进一步检查P[j]是否等于P[t]。唯有在 P[j] != P[t] 时，才能将t赋予next[j]；否则，需转而代之以next[t]。

这里讲的好：KMP 算法详解

BM 算法

KMP算法思路： 当前比对一旦失配，即利用此前的比对（无论成功或失败）所提供的信息，尽可能长距离地移动模式串
其核心为： 无需显式地反复保存或更新比对的历史，而是独立于具体的文本串，事先根据模式串预测出所有可能出现的失配情况，并将这些信息“浓缩”为一张next表。

BM算法思路： 模式串P与文本串T的对准位置依然“自左向右”推移，而在每一对准位置却是“自右向左”地逐一比对各字符。具体地，在每一轮自右向左的比对过程中，一旦发现失配，则将P右移一定距离并再次与T对准，然后重新一轮自右向左的扫描比对。为实现高效率，BM算法同样需要充分利用以往的比对所提供的信息，使得P可以“安全地”向后移动尽可能远的距离。

主体框架

int match ( char* P, char*T ) { //Boyer-Morre算法（完全版，兼顾Bad Character与Good Suffix）
	int* bc = buildBC ( P ); int* gs = buildGS ( P );	//构造BC表和Gs表
	size_t i = 0;	//模式串相对于文本串的起始位置（初始时与文本串左对齐)
	while ( strlen ( T ) >= i + strlen ( P ) ) {	//不断右移（距离可能不止一个字符）模式串
		int j = strlen ( P ) - 1;	//从模式串最末尾的字符开始
		while ( P[j] == T[i + j]）	//自右向左比对
			if ( 0 > --j ) break;
		if ( 0 >j )	//若极大匹配后缀== 整个模式串（说明已经完全匹配)
			break;	//返回匹配位置
		else //否则，适当地移动模式串
			i += __max ( gs[j], j - bc[ T[i+ j] ] );	//位移量根据BC表和Gs表选择大者
	}
	delete [] gs; delete [] bc;//销毁Gs表和BC表
	return i;
}

借助整数i和j指示文本串中当前的对齐位置T[i]和模式串中接受比对的字符P[j]。不过，一旦局部失配，这里不再是机械地令i += 1并在下一字符处重新对齐，而是采用了两种启发式策略确定最大的安全移动距离。为此，需经过预处理，根据模式串P整理出坏字符和好后缀两类信息。

坏字符策略

若模式串P当前在文本串T中的对齐位置为i，且在这一轮自右向左将P与substr(T, i, m)的比对过程中，在P[j]处首次发现失配：T[i + j] = 'X' != 'Y' = P[j]，则将'X'称作坏字符。
问题的关键是： 接下来应该选择P 中哪个字符对准T[i + j] ，然后开始下一轮自右向左的比对？

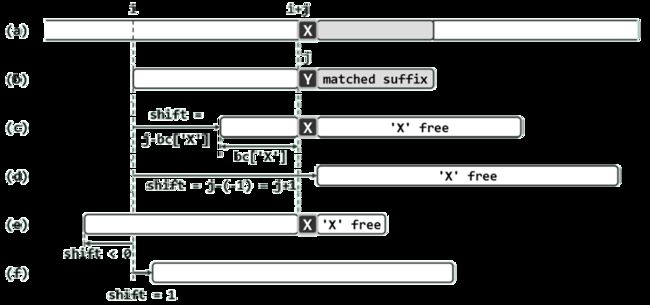
若P与T的某一（包括T[i + j]在内的）子串匹配，则必然在T[i + j] = 'X'处匹配；反之，若与T[i + j]对准的字符不是'X'，则必然失配。
如图 (c )所示，只需找出P中的每一字符 'X'，分别与T[i + j] = 'X'对准，并执行一轮自右向左的扫描比对。
对应于每个这样的字符'X'，P的位移量仅取决于原失配位置j，以及'X'在P中的秩，而与T和i无关！

bc[ ] 表

若P中包含多个'X'，仅尝试P中最靠右的字符'X'（若存在），可在确保不致遗漏匹配的前提下，始终单向地滑动模式串。
如图(c )所示，若P中最靠右的字符'X'为P[k] = 'X'，则P的右移量即为j - k。
对于任一给定的模式串P，k值只取决于字符T[i + j] = 'X'，因此可将其视作从字符表到整数（P中字符的秩）的一个函数：$$bc(c)=\{\begin{array}{ll}k& \text{若 p[k] =c，且对所有的 i>k 都有 p[i] != c}\\ -1& \text{若 p[ ] 中不含字符 c }\end{array}$$

预先将函数bc()整理为一份查询表，称作BC表。

若P根本就不含坏字符'X'，则如图(d)所示，应将该串整体移过失配位置T[i + j]，用P[0]对准T[i + j + 1]，再启动下一轮比对；
即使P串中含有坏字符'X'，但其中最靠右者的位置也可能太靠右，以至于k = bc['X']>= j。此时的j - k不再是正数，故若仍以此距离右移模式串，则实际效果将如上图(e)所示等同于左移；
如图(f)所示，简单地将P串右移一个字符，然后启动下一轮自右向左的比对。

实现

//*****************************************************************************************
// 0						bc['X']			 						m-1
// | 						| 										|
// .........................X***************************************
// 						    .|<------------- 'X' free ------------->|
//*****************************************************************************************
int* buildBc ( char* P ) {	//构造Bad Charactor Shift表: o(m + 256)
	int* bc = new int[256]; //Bc表，与字符表等长
	for ( size_t j = 0; j < 256; j ++ ) bc[j] = -1;	//初始化︰首先假设所有字符均未在P中出现
	for ( size_t m = strlen ( P )， j = 0; j <m; j ++ )	//自左向右扫描模式串P
		bc[ P[j] ] = j;	//将字符P[j]的Bc项更新为j(单调递增)——画家算法
	return bc;
}

对BC初始化之后，对模式串P做一遍线性扫描，并不断用当前字符的秩更新BC表中的对应项。因为是按秩递增的次序从左到右扫描，故只要字符c在P中出现过，则最终的bc[c]必将记录下其中最靠右者的秩。
运行时间可划分为两部分，分别消耗于其中的两个循环。前者是对字符表 $\sum$ 中的每个字符分别做初始化，时间量不超过$\mathcal{O}(|\sum |)$。后一循环对模式串P做一轮扫描，其中每个字符消耗O(1)时间，故共需O(m)时间。由此可知，BC表可在$\mathcal{O}(|\sum |+m)$时间内构造出来，其中$|\sum |$为字符表的规模，m为模式串的长度。

复杂度
BM算法本身进行串模式匹配所需的时间与具体的输入十分相关。
低于O(n)——实际情况，通常情况下；
最好：O(n / m)
最坏：O(n × m)——P总要完整地扫描一遍才发现失配并向右移动一个字符。

好后缀策略

坏字符：一旦发现P[j]与T[i + j]失配，就将P与T重新对齐于至少可使T[i + j]恢复匹配（含通配）的位置——有时计算效率将退化为几乎等同于蛮力算法。
坏字符策略仅利用了此前（最后一次）失败比对所提供的“教训”，成功比对的“经验”却被忽略了。

每轮比对中的若干次（连续的）成功匹配，都对应于模式串P的一个后缀，称作 “好后缀”。 （good suffix）

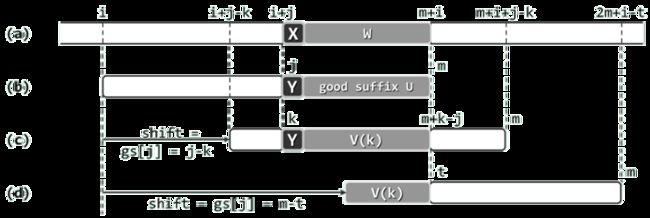
如图(a)和(b)所示，设本轮自右向左的扫描终止于失配位置：T[i + j] = 'X' != 'Y' = P[j]
若分别记：W = substr(T, i + j + 1, m - j - 1) = T[i + j + 1, m + i)，U = suffix(P, m - j - 1) = P[j + 1, m)
则U即为当前的好后缀，W为T中与之匹配的子串。
好后缀U长度为m - j - 1，故只要 j <= m - 2，则U必非空，且有U = W。

图( c)所示，设存在某一整数k，使得在将P右移j - k个单元，并使P[k]与T[i + j]相互对齐之后，P能够与文本串T的某一（包含T[m + i - 1]在内的）子串匹配，亦即：P = substr(T, i + j - k, m) = T[i + j - k, m + i + j - k)
于是，若记：V(k) = substr(P, k + 1, m - j - 1) = P[k + 1, m - j + k)
则必然有：V(k) = W = U
若值得将P[k]与T[i + j]对齐并做新的一轮比对，则P的子串V(k)首先必须与P自己的后缀U相互匹配——这正是从好后缀中“挖掘”出来的“经验”。

复杂度
同时结合以上BC表和GS表两种启发策略，加快模式串相对于文本串的右移速度。可以证明，对于匹配失败的情况，总体比对的次数不致超过O(n)

在兼顾了坏字符与好后缀两种策略之后，BM算法的运行时间为O(n + m)。

算法纵览

时间效率的变化范围

典型串匹配算法的复杂度

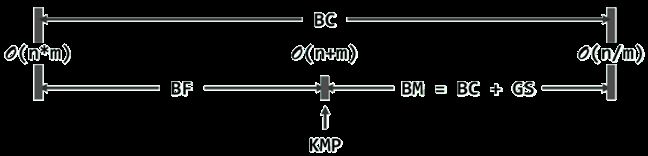
蛮力（BF）算法的时间效率介于O(n * m)至O(n + m)之间，而且其最好情况与KMP算法相当。

KMP 的优势在于，无论何种情况，时间效率均稳定在O(n + m)。因此在蛮力算法效率接近或达到最坏的O(n * m)时，KMP算法的优势才会十分明显。

仅采用坏字符启发策略（BC）的BM算法，时间效率介于O(n * m)至O(n / m)之间。其最好情况与最坏情况相差悬殊。
结合了好后缀启发策略（BC + GS）后的BM算法，则介于O(n +m)和O(n / m)之间。可见，在改进最低效率的同时，保持了最高效率的优势。

单次比对成功概率

随着单次比对成功概率（横轴）的提高，串匹配算法的运行时间(纵轴）通常亦将增加。

各种算法的最坏情况均可概括为：因启发策略不够精妙甚至不当，在每一对齐位置都需进行多达O(m)次成功的比对（另加最后一次失败的比对）。

将单次比对成功的概率记作Pr，纵坐标为运行时间，分为O(n / m)、O(n + m)和O(n * m)三档

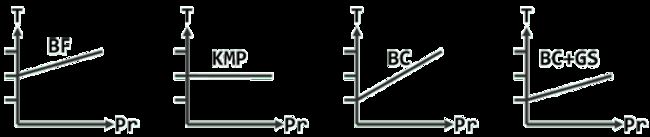
消耗于每一对齐位置的平均时间成本随Pr的提高而增加

字符表长度

在所有字符均等概率出现的情况下，Pr的取值将主要决定于字符表的长度 $|\sum |$，并与之成反比关系：字符表越长，其中任何一对字符匹配的概率越低。

这里讲的好：BM(Boyer-Moore) 算法详解