13. 机器学习 - 数据集的处理

Hi， 你好。我是茶桁。

上一节课，咱们讲解了『拟合』，了解了什么是过拟合，什么是欠拟合。也说过，如果大家以后在工作中做的就是机器学习的相关事情，那么欠拟合和过拟合就会一直陪伴着你，这两者是相互冲突的。

现在，让我们一起来思考一个问题：overfitting，过拟合产生的原因是什么？

如果这是在模型层面的话，参数过多还是过少？如果从数据层面来看，是过多还是过少呢？

好，我们来揭晓答案。如果模型层面思考，那是就是参数过多。如果从数据层面来看， 那是数据过少。

现在我们需要理解一件事情，这两个事情其实是一回事，数据量多和模型复杂其实是一回事。它背后的原因就是因为任何一个f(x)如果有很多的参数，拟合的时候随着这个参数数量越多，那么我们所需要的训练数据集也要增多。也就是说当模型非常复杂，参数特别多，只要数据量特别大，那就不算多。就说现有的数据量对于参数不够，训练力度不够。

这就好比是有一个天才的孩子，脑子极其聪明，就跟茶桁一样。哎， 这个孩子呢智商极其高，但是他想事情想的特别的复杂，结果他现在见到的事情都是太过于简单的东西。那么就不能把他的这个潜力发挥出来。

好，我们接着下一个问题：如何判断一件事情有没有发生过拟合或者欠拟合呢？

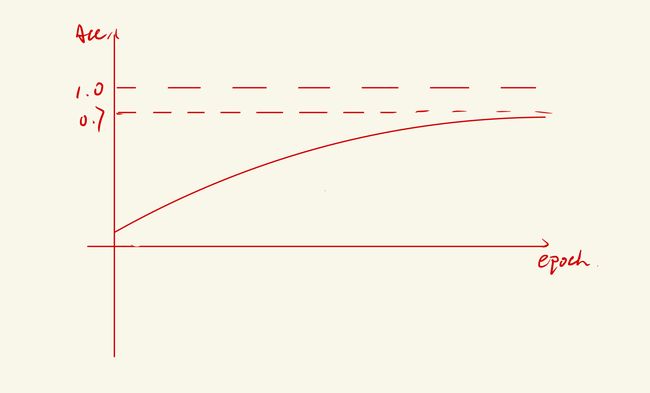
我们看这张图，假如这是一个2分类问题，咱们训练时候结果的准确度是0.7左右。那么大家想一下， 这个是过拟合还是欠拟合呢？

如果模型训练的时候效果还不错，快接近于1了，达到了百分之九十几。但是实际上用validation数据集去测的时候发现准确度下到百分之八十几，或者百分之七十几，总之就是比在训练的时候那个效果要差。这个就叫作过拟合。

咱们上节课给大家说的就是这个问题，机器学习的整个流程最终的目的不是为了把loss函数降到最低，我们要关心的是像recall，precition，这种信息才是最关键的。

Training data split

接下来，咱么要再讲几个机器学习里面极其重要的几个概念，第一个是数据集的切分(Training data split)。第二个是Normalization。第三个，Standardized。

其实上节课，咱们已经说过了数据集的切分问题。数据集切分最主要的原因是因为我们经常会遇见过拟合的情况，为了避免我们把所有的数据拿来不断的做training, 然后在使用的时候效果变得不好，那我们不如自己找一些数据出来做test sets，为了可以反复多次的去检验效果好不好，就增加了一个validation sets。

在真实环境下我们是怎么去做这样一件事呢？我们来简单的演示下：

from sklearn.model_selection import train_test_split
import numpy as np

sample_data = np.random.random(size(100, 5))

train, test = train_test_split(sample_data, train_size=0.8)
train

---
array([[1.55582066e-01, 8.19437761e-01, 3.54628257e-02, 5.53248385e-01,
        4.23785508e-01],
...
       [7.24889349e-01, 1.23458057e-01, 9.74101303e-01, 1.72605427e-01,
        6.59164912e-01]])

非常的简单，我们来看，sklearn里自带了这种分割方法。我们随机了100行5列的数据，然后使用train_test_split将其分割成train和test两份，在后面的参数内设置了百分位。

这样，这个数据就做了一个拆分。值得注意的是，给大家教一个小技巧，这是第一种方法：split。其实不只是sklearn， pytorch和keras也都有split方法。

但是我们去看一下源码会发现， 这个split方法是没有validation，它的输出只有train和test两部分。

为了解决这个问题，我们可以用一个简单的方法。这次我们使用Numpy。

indices = np.random.choice(range(len(sample_data)), size=int(0.8*(len(sample_data))), replace=True)

indices

---
array([39, 65,  5, 13, 69,  8, 49,  2, 16, 16, 28, 28, 99, 13, 64, 76, 55,
       96, 12, 87, 81, 55, 96, 54, 94, 15, 44, 23, 17, 76, 98, 84, 21, 50,
       62, 58, 21, 95, 22,  3,  6, 35, 93, 34, 68, 49, 29, 81, 58, 45, 95,
       26, 21, 97, 43, 30, 40, 52, 93, 34, 17, 71, 76, 38, 92, 62, 21, 98,
       56, 28, 54, 39, 15, 17, 62, 81, 61,  4, 51, 71])

这里我们等于是把它的整体的顺序打乱，后面的replace就是可以重复的去取。这样我们就随机的取了一些下标。

这是一个比较简单的方法, 那么我们为什么要设置replace=True呢？当数量特别大的时候，多取几个少取几个其实不是很影响，另外replace的话，他内部的那个随机的算法其实是不一样的，速度会快的多。以后如果遇到类似的事情，你也可以去用这个方法去做它。

Normalization

除了这个以外， 做机器学习的时候，要做数值的归一化(Normalization)和标准化(Standardized)这样一个动作。

我们这么做的目的是什么呢？假设我们现在有多个特征的数据集，不过我们注意到一点，就是这些特征值跨越的范围是无法进行比较的。

比如，一个特征在1和10之间变化，但是另外一个实在1和1000之间变化。如果我们忽略了这一点而直接进行建模，模型分配给这些特征的权重将会受到严重影响，模型最终会为较大的变量分配较高的权重。

现在要解决这个问题，将这些特征置于相同或者至少是可比较的范围内，那就需要对数据做一个数据归一化。

归一化的目标是讲数据缩放到特定范围内，一般来说是[0,1]或者[-1,1]之间。这有助于消除不同特征之间的尺度差异，确保它们对模型的权重贡献大致相等。

数据归一化对于每个特征x，归一化后的值Xnormalized计算如下：

其中min是特征的最小值，max是特征的最大值。这个操作确保了数据的最小值映射到0， 最大值映射到1.

在数据预处理过程中，首先计算每个特征的最小值和最大值，然后使用上述公式对数据进行归一化。这通常通过一次遍历数据来实现。

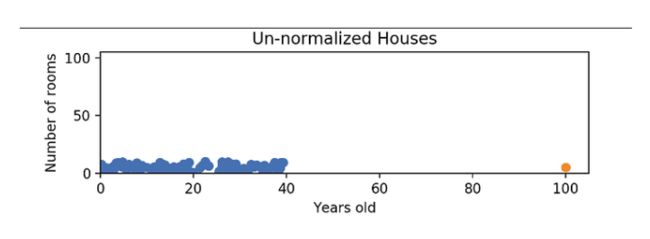
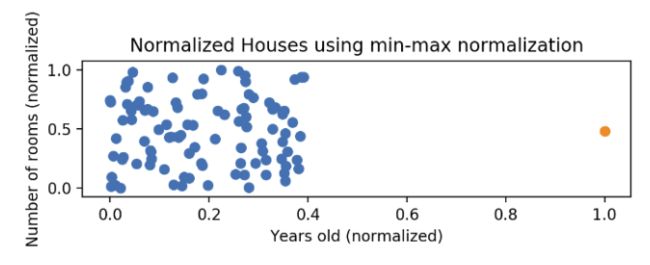
在进行归一化的时候，我们所使用的那个公式会有一个缺点，就是它并不能很好的去处理异常值。比方说，如果有0到40之间的99个值，其中一个值为100， 则这99个值讲全部转换为0到0.4之间的值。这些数据和以前一样被压缩！下图就是个示例：

这些数据在进行归一化之后，解决的是y轴上堆集的问题，但是x轴上的问题依然存在，就像途中橙色点那个异常值：

关于这个知识点，我们来看一个极其简单的例子：

some_large_number = [23421421,42155151,25531238,21826139, 32189732, 32103721]
def normalize(x):
    return (x - np.min(x)) / (np.max(x) - np.min(x))
ic(normalize(np.array(some_large_number)))

---
array([0.07847317, 1., 0.18225672, 0., 0.50979325, 0.5055623 ])

我手动定义了6个比较大的数字，在进行处理之后我们看到了，都变成了一些特别小的数字。

同样的，对于特别小的数字，它一样可以进行处理：

some_small_number = [0.00000231213,  0.0005600321, 0.0000041412892, 0.000987890576, 0.0000578921764]
ic(normalize(np.array(some_small_number)))

--- 
array([0., 0.56588085, 0.00185592, 1., 0.05639333])

Standardized

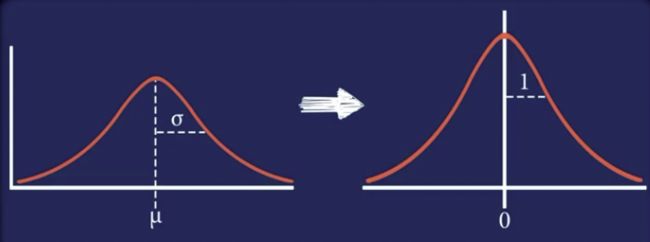
那么还有就是标准化，对于标准化，其目标是讲数据转化为均值为0， 标准差为1的分布，也就是标准正态分布。这有助于处理偏斜分布的数据，并确保数据的均值和方差在模型中起到合适的作用。

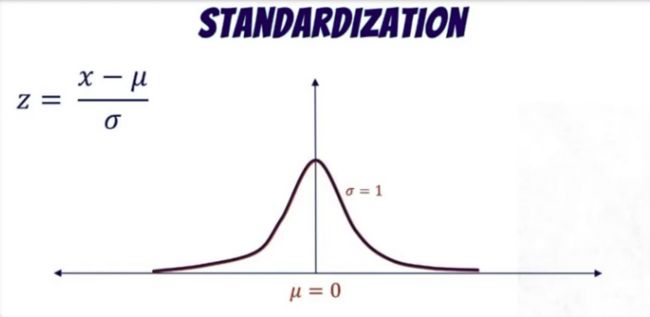
那对于每一个特征x，标准化的值z计算如下：

$\mu$是特征的均值，$\sigma$是特征的标准差。这个操作使数据的均值为0，标准差为1。

在数据预处理的过程中，首先计算每个特征的均值和标准差，然后使用上述公式对数据进行标准化处理。标准化后的数据具有均值0和标准差1，这有助于模型更好的理解和捕捉数据之间的关系。

无论是归一化还是标准化，其实依据来源都是基于线性代数的变化理论，这确保了归一化和标准化后的数据分布具有特定的属性，这些属性对于机器学习算法的表现非常有帮助。

我们来看一个标准化的例子，为了让大家更为明显的了解其意义，我做了一些非常大的数据，但是每一个都不相同。这些数据有一个特点，就是相对于数值本身的大小来说，几个数值之间的差距可以说是非常微小的：

some_dense_number = [47238941, 47238946, 47238951, 47238931, 47238949, 47238936]
def standarlize(x):
    return (x - np.mean(x))/ np.std(x)

ic(standarlize(np.array(some_dense_number)))

---
array([-0.18752289,  0.51568795,  1.2188988 , -1.59394459,  0.93761446, -0.89073374])

我们定义的数据实际上是非常密集，但是使用standarlize公式之后，就变得比较的分散，比较的均匀了。这个情况还是很多的。

ONE-HOT

在讲完training data split, normalization, Standardized之后，我们来看下面一点： ONE-HOT。

为什么要用ONE-HOT？ 我们都直到，咱们计算机里其实都是数字，包括视频，图片，声音，文字等其实都是数字。

数字和数字其实是不一样的。比如，有一群人分成了4组：

然后有一个女生的GPA是4:

那么分组的4和GPA的4有什么区别？最明显的一个区别就是，分组的4只是一个组名，那么假如和1组交换组名并没有太大的关系，但是GPA的这个4如何和1交换一下，那就从4分变成1分了，那这两个是不能相互变换的。本质上，其区别就是一个可比一个不可比。

我们也就发现了，数字其实是有区别的。这个世界中，数字其实可以分成两类：

第一类叫作Categorical，叫作分类数据，也被称为离散数据或名义数据。它们之间不能被比较，也不能被排序，这些数字也仅仅是表示一个和另外一个不一样。就我们刚才讲人群分为1、2、3、4组，其实分成A、B、C、D组也是一样的，只是表示区别。

第二类是Numerical，数值数据，也被称为连续数据。这个是可以比较的，也可以进行排序。这种数据包括可以用来进行数学运算的实数值。

Numerical还可以进一步分为整数和浮点数。

知道了这一点之后，那我们以后遇到类似的情况不要随便的做加减乘除。

那我们有了Categorical和Numerical这两种类型之后，会对我们有一些什么比较重要的影响？

如果现在有一个函数，这个函数输入一个x向量，它输出就是分为一个Categorical和numerical。

输出是0-1这样一个数字，是一个典型的逻辑回归。

假如有一个人在北京，年龄27，性别男，月入一万二。然后还有一个人，生活在安徽，年龄28，性别女，月入8,000。第三个住在上海，年龄28，性别男，月入一万三。

1. 北京, 27, 12000
2. 安徽, 28, 8000
3. 上海, 28, 13000

我们注意这三组数据，如果现在做一个向量表证。

关于地域，我们常常使用的方法包括邮编排序，或者使用拼音排序。假如这里我们就使用拼音首字母来进行排序，安徽假如是1， 北京是2， 上海是27。

我们的数据进行向量化可能就会变成下面这样：

# 1. 北京
vec(2, 27, 12000)
# 2. 安徽
vec(1, 28, 8000)
# 3. 上海
vec(27, 28, 13000)

然后我们定义一个函数：

def f(x):
    return (0, 1)

非常简单一个函数，返回表示对某一样东西买还是不买。

函数的实现过程就是类似于wi * xi + b这种形式。

我们观察向量发现，就向量值而言，北京这个人和安徽这个人之间的向量差比北京和上海这两人之间的向量差还要小。

$$|v_1-v_2|<|v_1-v_3|$$

我们假如说经过函数f(x)之后，输出的结果分别为Y1, Y2, Y3。因为v1和v2离的更近，就会有一个结果，Y1和Y2的结果其实会更相似。但是其实呢，这种结果完全不对。这样乱比其实会出问题，会让程序出错。

我们现在知道，这其实是一个Categorical的问题。为了解决Categorical的这种问题，我把Categorical改成这样：

北京: [1, 0, 0]
安徽: [0, 1, 0]
上海: [0, 0, 1]

改成这样之后这个向量就变成了这样：

# 1. 北京
vec(1, 0, 0, 27, 12000)
# 2. 安徽
vec(0, 1, 0, 28, 8000)
# 3. 上海
vec(0, 0, 1, 28, 13000)

向量变成这样之后，就解决了我们刚刚说的那个问题。不会导致因为分类过于相似让北京和安徽向量相似度大于北京和上海的相似度。

对于这样一个向量，三组数据中改变的那个值向量值就都为$\sqrt{2}$，这一种方式就被称为ONE-HOT。

那这种方式也是存在问题的，目前我们只去考虑三个城市。可是当存在成百上千个城市的时候，比如说Google地图等等这些应用。

当城市越来越多的时候，那它的维度就会变得很高：

Beijing     = [1, 0, 0, 0, 0, 0, ..., 0]
Shanghai    = [0, 1, 0, 0, 0, 0, ..., 0]
Chengdu     = [0, 0, 1, 0, 0, 0, ..., 0]
Shenzhen    = [0, 0, 0, 1, 0, 0, ..., 0]
...

我们想想一下，这样得有多少个地址？可能空间会极其的大，你这样的话数字光存起来得上亿个存储单元。

ONE-HOT就有这样的问题：

1. 耗费空间
2. 数据量大，更新起来，效率极低
3. 遗漏了很多重要新息

就比如，我们再增加几个人如下：

- 重庆 27 9000
- 成都 26 8500
- 呼和浩特 26 8500

在这三个城市中，我们脑子里其实就直到，重庆和成都是非常接近的。但是在ONE-HOT里是体现不出来，其向量值依然是根号2。

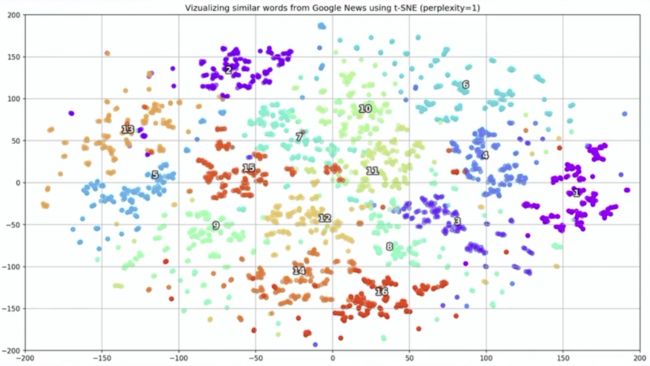
为了解决这些问题，人们就用到了更先进的一种方法：embedding，
叫作嵌入。

嵌入就是把东西放在固定的位置，这个就是嵌入的意思。在这里，就我们空间中如果有几个实体NTT1 NTT2 NTT3，我们把这些实体放到这个空间中，要达到一个结果就是如果实体1和实体2的相似度小于实体1和实体3的相似度，这个相似度我们可以自己来定义，比如成都和重庆的生活方式，再比如重庆和北京都是直辖市。

在这个问题场景下，我们期望达到的结果是如果这两个实体相似那么他们在空间中的距离也接近。

如何实现Embedding, 这本身是一个研究领域, 是现在非监督学习，表证学习里面非常重要的一个研究领域，属于比较高级的一个知识点。

第二就是如果之后咱们学NLP，那么一定会讲到这个，因为要把文本单词进行嵌入，到时候会学到。如果是学推荐系统的，大家也会学什么Graph embedding，基于图的用户行为。

那之后咱们学习NLP，其基础就是Embedding。关于这个问题，我们其实目前了解到这里就行了。再往下延展下去，又是一个专门的研究话题。延展后的这个问题解决方案，在我们后面的课程中会等着大家去学习。

我们再来看看ONE-HOT的实际展示：

array = ['北京','上海','广州','宁夏','成都','上海','北京']

def one_hot(elements):
    pure = list(set(elements))
    
    vectors = []

    for i in elements:
        vec = [0] * len(pure)
        vec[pure.index(i)] = 1
        vectors.append(vec)

    return vectors
ic(one_hot(array))

---
one_hot(array): [[0, 0, 0, 1, 0],
                [0, 0, 0, 0, 1],
                [0, 0, 1, 0, 0],
                [1, 0, 0, 0, 0],
                [0, 1, 0, 0, 0],
                [0, 0, 0, 0, 1],
                [0, 0, 0, 1, 0]]

其实ONE-HOT非常简单，但是基本上很多面试官都喜欢问这个问题。这个问题主要就是一个可以考察一下你的Python编程能力，其次他可以去问一下你one hot的作用是什么，再者还可以往后问你one hot有什么缺点，怎么解决等等。一个问题就可以问你半个小时。

补充：SOFTMAX 和 CROSS-ENTROPY

好，在本节课最后，我们来做一个前面课程的补充，在今天才想起来，有一个相关的点遗漏了没有讲到。

之前我们讲过逻辑回归的loss函数：

假如y=1， loss可以等于-log(yhat), 如果y等于0， loss就可以写成-log(1-yhat)。两个合并后就组成了最终的loss函数：

$$loss=-(ylog\hat{y}+(1-y)log(1-\hat{y}))$$

那么，这个是解决二分类的，结果才不是0就是1。现在的问题就是如果我们要解决多分类的问题怎么办。

如果要解决多分类的话，需要把x变成一种能预测多分类的东西。那最终yhat可以表示成 $\hat{y}=(0.25,0.20,0.75)$。

也就是，现在要表示三个类别，那我们可以用三个小数来表示。这个向量经过各种计算，如果能够变成一个三维的向量，然后再去优化里边的参数就可以做到。

那这也就代表的是类别1、类别2、类别3的概率。ytrue就可以写成yhat的形式，就变成(1, 0, 0)。

就是我们给定一个$x$, 它实际的y是(1, 0, 0)， 那么yhat就是估计值等于0.25、0.20和0.75。然后对比一下两组数据之间的差别，这样我们就可以优化其中的形成参数(w, b)。

通过不断优化, 就可以计算到更接近于(1, 0, 0)这样的值。

首先就是怎么样把x向量变成3维的。

这个其实不难，如果x是10维的，110。那么给他再乘以一个
103的矩阵，它最后就会变成一个1行乘3列的矩阵。

那么现在假如说现在有这样一个x:

x = [1231, 12314, 4341, 1542, 4123, 4512, 3213, 1241, 1231, 6842]

然后我们来做这样一件事:

x = np.array(normalize(x))
weights = np.random.random(size=(10, 3))
np.dot(x, weights)

---
array([0.86907231, 1.32234548, 0.88170994])

这样，我们就生成了一个维度是3的一串数字。在机器学习里面，我们把这个叫做算子：logits。

现在我们将一个10维的x变成了一个3维的logit，下一步我们就要考虑，怎么将这个logit变成一个概率分布呢？

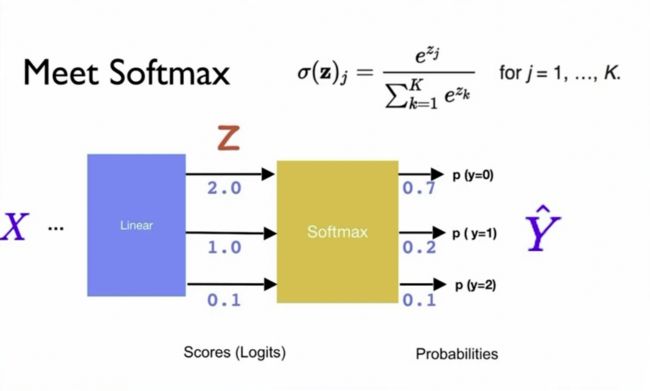
我们就要用到一个和逻辑函数特别像的一个函数，Softmax：

我把它写出来:

logits = np.dot(x, weights)

def softmax(x):
    return np.exp(x) / np.sum(np.exp(x))

ic(softmax(logits))

---
array([0.27884889, 0.43875588, 0.28239524])

这样，我们输入的是logits，输入到Softmax，输出的就是概率了。

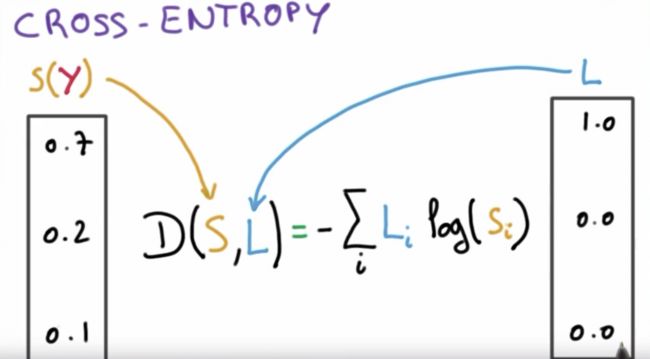
输出成概率之后，我们定义一个依然和逻辑函数很像的一个函数，叫做Cross-entropy。

我们刚才使用softmax输出的数组就是概率，也就是估算的yhat。这个Cross-entropy的loss就是：

求得loss，然后再对x求偏导，就可以通过梯度下降让输入的x得到和真正的y相近的yhat。

那我们将cross-entropy也写一下：

def cross_entropy(yhat, y):
    return -np.sum(y_i * np.log(yhat_i) for y_i, yhat_i in zip(y, yhat))

现在我们需要一组真正的y，也就是真实值，和我们预测房价时所使用的真实值是一样的东西，只是现在我们的y的维度不太一样：

y = [0, 1, 0]

接着我们使用cross_entropy将我们之前使用softmax计算的概率分布和真实的y放进去：

ic(cross_entropy(softmax(logits),y))

---
1.040664959870481

这个时候我们就得到了一个loss值。

我们现在去给weights求偏导。然后通过不断的迭代，就能找到一组wi， 和x进行点乘就能够生成和y接近的值。

以上这些就是softmax和cross-entropy的作用。

cross-centropy就是用来衡量产生的yhat和y之间的相似程度差距的。 Softmax是把任意的一组数字变成概率分布，然后这个概率分布就可以送到loss函数里面和实际上的y进行对比。

Softmax有这么几个特性，它的结果是一个典型的概率分布。还有就是Softmax中有e的n次方，可以把Max变得更大。除了把Max变得更大，还保留原来小的数字。

理论上完全可以找别的函数代替，计算机里边很多东西，只要好用就行。这就是放大特征，正是面对多分类任务的一个做法。

Softmax在实现的时候有个坑稍微要注意一下，在实现的时候我们多加一句：

def softmax(x):
    x = np.array(x)
    x -= np.max(x) # 多加这么两句
    return np.exp(x) / np.sum(np.exp(x))

ic(softmax(logits))

首先，如果x的输入是一个array就不用管了，但是如果不是，我们就要强制转换一下。

下一句代码是因为e的x次方可能非常的大，但是我们计算机的存储是有限的，最大只能表示2^63的数字，再大就表示不了了。所以我们就需要这样一段代码来处理一下，让最后结果的数字不要那么大。

好，那这一节课的内容到这里也就结束了。