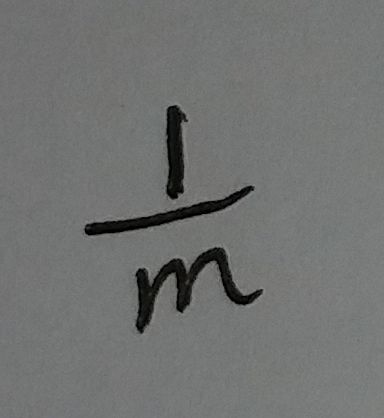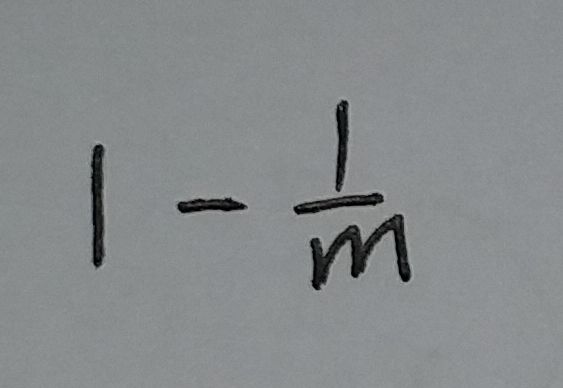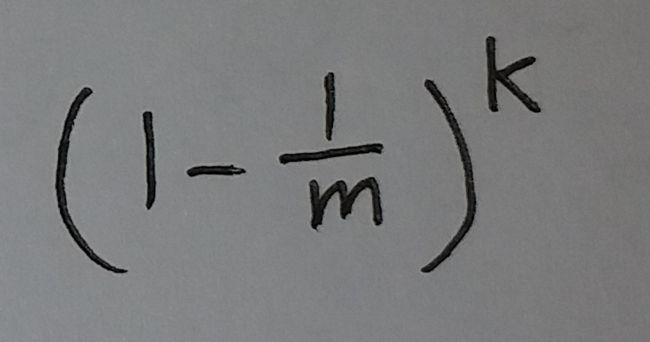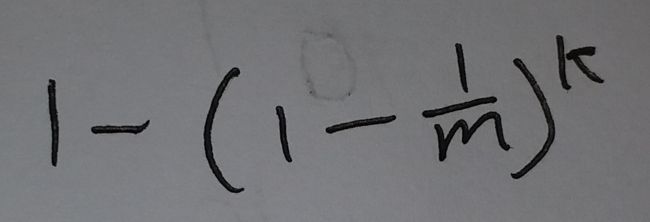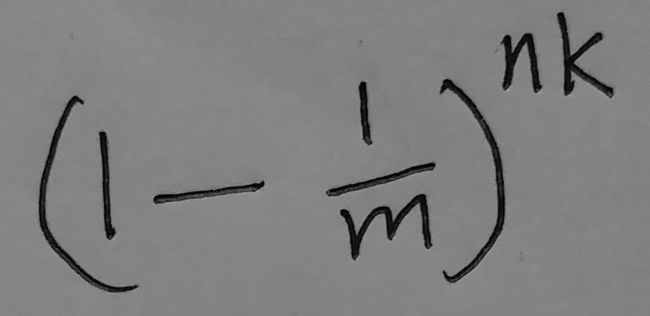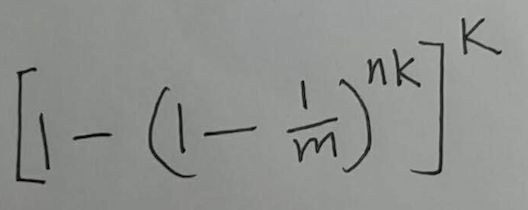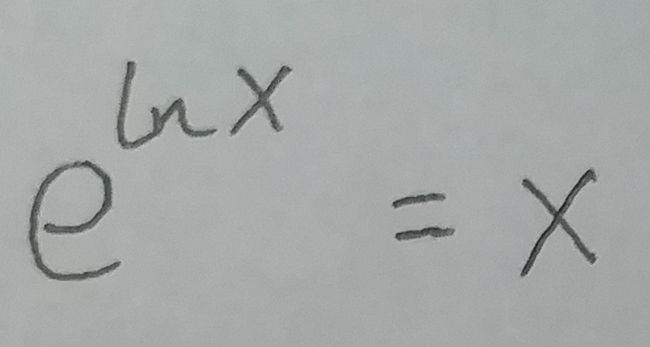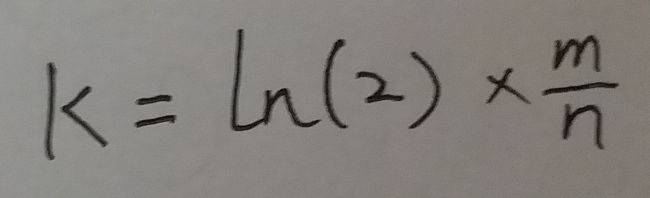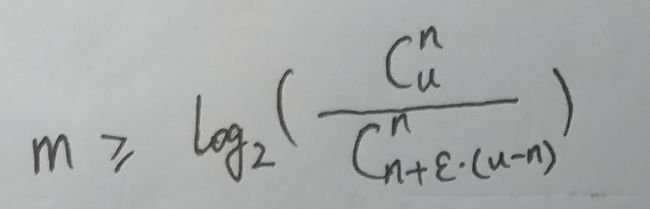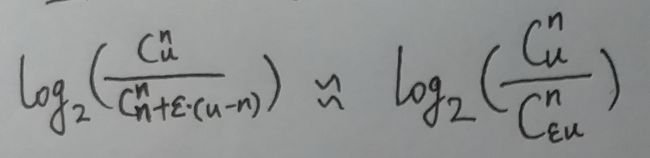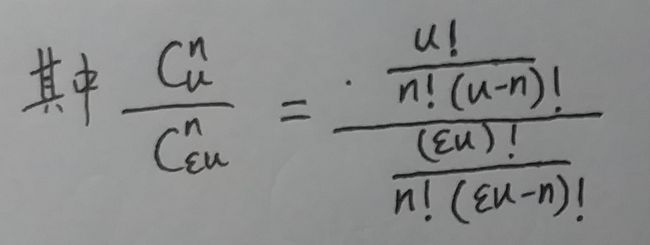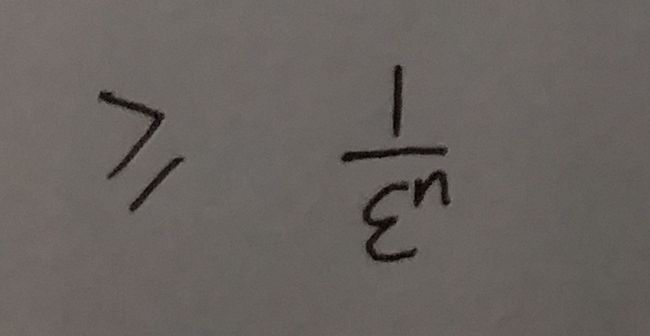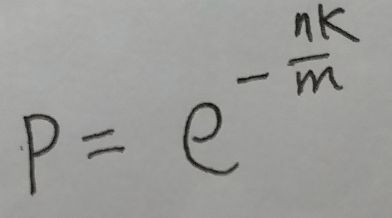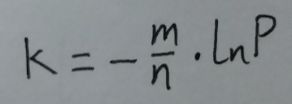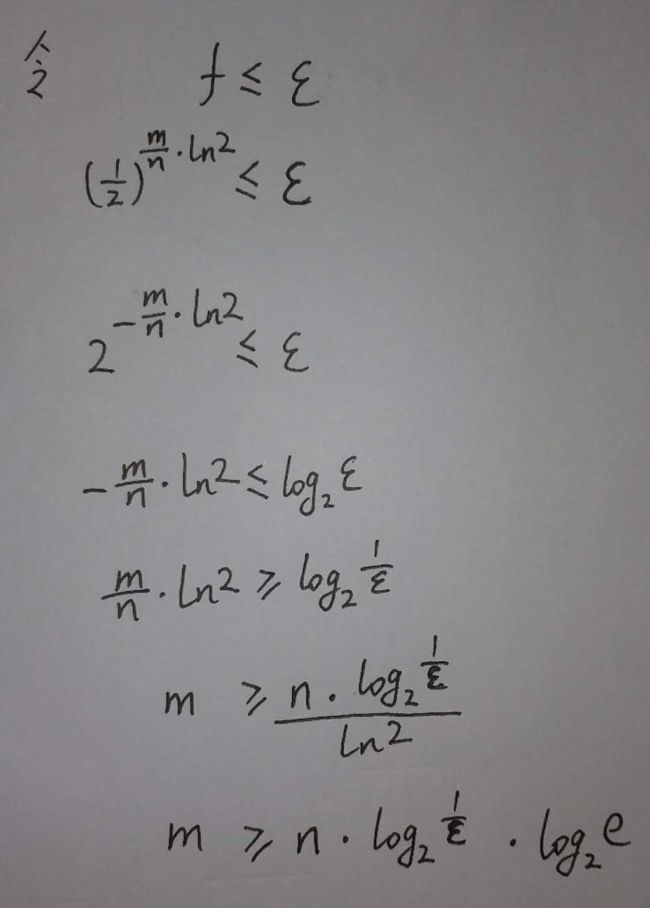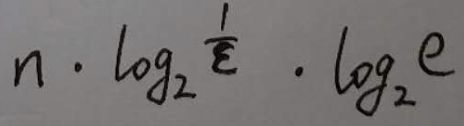布隆过滤器雏形
未完待续.....
计算错误率
现在有一个空额布隆过滤器, 过滤器里的bit array的大小是m. 咱来插入一个元素. 这次插入过程中的第一个hash函数会算出一个位置, 然后把这个位置设置为1. 此时如果在这个过滤器中随机选取一个位置, 这个位置的值是1的概率为:
这个位置的值是0的概率为:
插入这个元素需要进行k个hash运算, 然后把相应的位置的值都改为1. 这个元素插入完之后, 从这个过滤器中, 随机取一个位置, 这个位置的值是0的概率为:
这个位置的值是1的概率为:
如果在这个布隆过滤器中, 插入了n个元素. 然后随机取其中一个位置, 这个位置的值是0的概率为:
这个位置的值是1的概率为:
(式⑥)
现在这个布隆过滤器里有n个元素. 现在来了一个新元素. 这个新元素用k个hash函数, 分别计算了hash值, 结果k个位置在之前就已经被设置为了1. 这就是错误了, 把不存在于集合中的元素, 判断为了在集合中, 被称为假阳性. 这种情况的概率是:
上面式子整理一下指数nk, 就等价于下面这个式子:
(式⑧)
这是一个极限公式:
上面的式⑧可以根据这个极限公式, 转化为下面这个式子:
(式⑨)
函数 f 就是误判率了.
最优的哈希函数个数
根据上面这个公式, 可以将 f 转化为:
(式⑩)
式10的表达式太长了...咱们引入两个新的符号p 和 g :
咱们回到话题"最优的hash函数个数k".
k是自变量, f是因变量. 让 f 取值最小的那个k值, 就是最有解. 也就是最优的hash函数个数.
让f最小, 也可以转化为: 让g最小. 所以咱们求一下"令g值最小的k值"
(式⑪)
把上面这个k带入到g中, 可以得到:
想让g取最小值, 其实就是让 ln(p) * ln(1-p) 取最大值.
当p = 1/2 时 . ln(p) * ln(1-p) 取最大值. 也就是 g 取最小值. 也就是 f 取 最小值.
将 p = 1/2 带入式11, 得:
位数组的大小
咱们模拟一个场景: 使用布隆过滤器来做URL的过滤. 将含有不良信息的URL作为黑名单, 存入到布隆过滤器中, 进行过滤.
咱么假设全世界有u个URL. 其中有n个是含有不良信息的. 布隆过滤器的 `位数组` 的大小是m.
咱们把这n个黑名单URL插入到布隆过滤器中.
这n个URL, 在被访问时, 会直接被布隆过滤器判定为含有不良信息的URL.
但是如果布隆过滤器的误判率是ϵ的话, 那么会有 ϵ*(u - n) 个元素, 明明是正常的URL, 却会被布隆过滤器认定为是含有不良信息的URL.
在这个场景中, 布隆过滤器的作用就是判断URL, 判断并过滤掉有不良信息的URL. 他会正确地判断出n个黑名单URL, 还会误判ϵ*(u - n) 个URL.
所以这个布隆过滤器, 会过滤 n + ϵ*(u - n) 个URL. 而当前的布隆过滤器中, 实际只有n个元素.
所以当前的布隆过滤器的`位数组`的状态, 可以表示的集合数量为:
(式⑫)
式⑫只是在刚才的那个特定条件下的`位数组`可以表示的集合数量.
如果咱们改变布隆过滤器的其中一个位. 那么此时就表示了新的ω个集合.
刚刚讲了, 只要改动其中一个位, 新的`位数组`就可以表示新的ω个集合. m 位的`位数组`共有 2m 个不同的组合来进行改变. 进而可以推出, m位的`位数组`可以表示的集合数量为:
全集中 n个元素的集合总共的数量为:
要让 m 位的位数组能够表示所有 n 个元素的集合, 必须有:
整理一下, 也就是:
如果n 远小于 ε·u
接下来咱们对于上式中的真数进行计算:
所以, 式⑬中的:
于是我们得出结论1 : 在错误率不大于 ϵ 的情况下, m 至少要等于 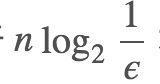 才能表示任意 n 个元素的集合.
才能表示任意 n 个元素的集合.
在计算错误率的小节中, 最后得出了式⑨:
在计算最优函数个数的小节中, 定义了:
而且在最后p = 1/2 时, 为最优函数个数.
又根据上面小节的式⑪:
在取最优函数个数的时候:
咱们令 f ≤ ε
于是我们有了结论2: 如果想采用最优函数个数, 那么m值就得是结论1的 1.44倍.
总结一下结论1 和 结论2 :
(式①②③④⑤⑥⑦⑧⑨⑩⑪⑫⑬⑭⑮⑯)
[1].<<数学之美>>第23章. 作者: 吴军
[2].https://blog.csdn.net/maoke2005191/article/details/78977277