leetcode鸡蛋掉落问题
转自:https://github.com/Shellbye/Shellbye.github.io/issues/42
前几天尝试了一下leetcode中文版通过率最低的一个题( #41 ),后来发现是关于动态规划的题目,然后听几个人说动态规划是算法题里面比较难的一类,于是就有找了一个动态规划的题目,自己思考了很久,最后依然是通过理解网络上的资源才有了着手之处。
题目
你将获得 K 个鸡蛋,并可以使用一栋从 1 到 N 共有 N 层楼的建筑。
每个蛋的功能都是一样的,如果一个蛋碎了,你就不能再把它掉下去。
你知道存在楼层 F ,满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎,从 F 楼层或比它低的楼层落下的鸡蛋都不会破。
每次移动,你可以取一个鸡蛋(如果你有完整的鸡蛋)并把它从任一楼层 X 扔下(满足 1 <= X <= N)。
你的目标是确切地知道 F 的值是多少。
无论 F 的初始值如何,你确定 F 的值的最小移动次数是多少?
示例 1:
输入:K = 1, N = 2
输出:2
解释:
鸡蛋从 1 楼掉落。如果它碎了,我们肯定知道 F = 0 。
否则,鸡蛋从 2 楼掉落。如果它碎了,我们肯定知道 F = 1 。
如果它没碎,那么我们肯定知道 F = 2 。
因此,在最坏的情况下我们需要移动 2 次以确定 F 是多少。
示例 2:
输入:K = 2, N = 6
输出:3
示例 3:
输入:K = 3, N = 14
输出:4
提示:
1 <= K <= 1001 <= N <= 10000
错误的第一感觉
计算机这个领域,在成为真正的大神之前,大多数人的第一感觉都是不准的,因为这是一个极度理性的领域,至于那些已经封神的大牛,他们几乎已经通过长久的练习与见多识广把很多理性的耗时的分析都转化成了O(1)的感觉。
在最初看这个题目的时候,我的第一反应就是二分查找,简单来看,这个题目就是通过二分查找来确定F的索引,于是第一反应就是logN。但是仔细一看就发现是不对的,那必须啊,因为还有已知条件(K)还没用上呢!根据初高中的理科经验可知,如果题目中有一些已知条件你没用就把题目做完了,那很大概率是你题目做错了(也有可能你是天才)。那么在这个题目中,问题出在哪里呢?这个题目与二分查找不一样的地方在于它的每一次比较大小——即扔鸡蛋——都是有代价的,这种代价就是因为鸡蛋摔破而导致的后面比较机会的减少。下面我就来看看“正确”的解法。
暴力解法
相比上一个题目( #41 ),这个题目暴力解法也不是很简单就能想到的——起码我是没想到。当然,看过答案之后就会觉得“很明显”了,这样的流程其实是不科学的,下面我就尝试引导读者一步步走向答案。
首先,我们来看扔鸡蛋这个事儿本身,假设在N层的高楼中有K个鸡蛋,这个时候我们在n层扔了一个鸡蛋,那么这一次动作,把整个高楼其实就分成了两部分,一部分是1楼到n楼,这是一个层高为n的新楼,我们暂时叫它一号楼;另一部分是n+1到N楼,这是一栋新产生的层高为N-(n+1)+1=N-n的新楼,我们叫他二号楼。
然后,我们来看刚扔下去的鸡蛋,如果它碎了,说明楼层太高(起码高于F),那么F应该是在一号楼,那么我们就带着剩下的K-1个鸡蛋去一号楼继续,当我们站在一号楼的某一层的时候,其实和最开始是一样的(递归的信号)。如果鸡蛋没碎,说明楼层不够高(低于F),此时我们要去二号楼,但是这里有一点点需要注意的,就是我们在二号楼的某一层的时候,其实该层在原始的楼里是要比当前楼层高n层的,其他同理。
最后,因为我们是要找无论 F 的初始值如何的条件下的查找次数,所以我们要在一号楼和二号楼各自的查找次数中选择那个最大的值,用计算机语言描述整个过程,就是
searchTime(K, N) = max( searchTime(K-1, X-1), searchTime(K, N-X) )
其中的X就是我们刚才扔鸡蛋做在的楼层,它具体是哪一层并不重要。对于从1到N的每一个X,都可以计算出一个对应的searchTime的值,在这N个值中,最小的那个就是本题的答案了!
class Solution {
public int superEggDrop(int K, int N) {
return Solution.recursive(K, N);
}
public static int recursive(int K, int N) {
if (N == 0 || N == 1 || K == 1) {
return N;
}
int minimun = N;
for (int i = 1; i <= N; i++) {
int tMin = Math.max(Solution.recursive(K - 1, i - 1), Solution.recursive(K, N - i));
minimun = Math.min(minimun, 1 + tMin);
}
return minimun;
}
}
上面的这个方法有多暴力呢?通过推导式我们发现它和斐波那契数列第N项的计算方法(Fib(n) = Fib(n-1) + Fib(n-2))类似,那么,这个东西的时间复杂度又怎么计算呢?对于第N项 Fib(n) = Fib(n-1) + Fib(n-2),这个计算本身就是一个加法,其时间复杂度是O(1),但是其中包含了第N-1和第N-2两项,他们又同理本身需要一个O(1),且也分别包含了第N-1-1、第N-1-2和第N-2-1、第N-2-2四项,以此类推,这就是一个满二叉树的节点总数求和(如图),即O(2^n),同样的,其空间复杂度很低,仅仅是O(1)。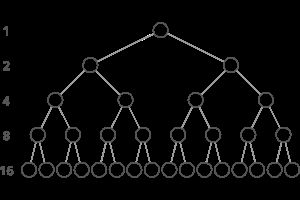
空间换时间解法
上面的计算之所以时间复杂度高,与递归版本的斐波那契数列一样,就是因为重复计算了很多遍底部节点的值,为了加快这个计算过程,一个简单的提升方法就是拿空间换时间,把计算的中间结果都存储起来,后面直接查表即可。
class Solution {
public:
int superEggDrop(int K, int N) {
int middlevalue[K+1][N+1];
for(int i=1;i<=N;i++){
middlevalue[0][i]=0;
middlevalue[1][i]=i;
}
for(int i=1;i<=K;i++){
middlevalue[i][0]=0;
}
for(int k=2;k<=K;k++){
for(int n=1;n<=N;n++){
int TminDrop=N*N;
for(int x=1;x<=n;x++){
TminDrop = min(TminDrop, 1 + max(middlevalue[k - 1][x - 1], middlevalue[k][n - x]));
}
middlevalue[k][n]=TminDrop;
}
}
return middlevalue[K][N];
}
};
这个解法利用了一个二维数组存储了部分计算结果(空间复杂度O(KN)),使得时间复杂度降低到了O(KN^2)。但是依然是一个平方级别的时间复杂度,不够快,还能优化吗?
基于二分查找的动态规划法
最开始的时候,我们就想到了二分查找,但是因为发现不对,就果断抛弃了,事实上它还是有利用价值的。在上一个O(KN^2)的算法中,我们拿着K个鸡蛋检查了每一个楼层来寻找F,但是事实上这并不是必须的,为什么呢?我们来看我们上面总结的这个递归的等式
searchTime(K, N) = max( searchTime(K-1, X-1), searchTime(K, N-X) )
现在我们令T1 = searchTime(K-1, X-1),T2 = searchTime(K, N-X),其中,T1是随着X的增长而增长的,T2是随着X的增长而降低的,如下图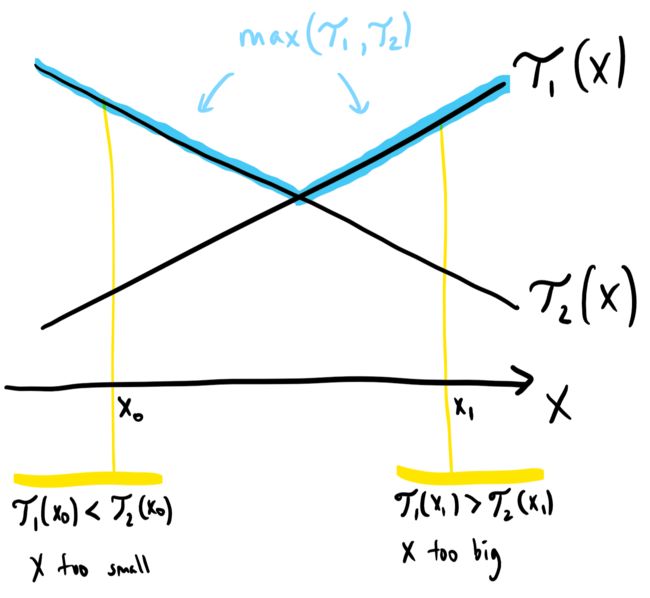
其中蓝色描出来的部分,就是searchTime(K, N)了,我们可以看出来它是局部有序的,所以可以考虑二分查找之!这里有一些与简单二分查找不一样的地方,就是在简单二分查找中,我们拿到输入数组A和它的下标low,high,mid之后,比较大小直接就是用下标读取数组的值A[low] < A[mid],但是在我们这个二分查找中,这个值是需要依赖与本题逻辑相关的一些计算的,具体看代码
class Solution {
public:
unordered_map cache;
int superEggDrop(int K, int N) {
if (N==0 || K==0)
return 0;
if (K==1)
return N;
int key = N * 1000 + K; // K <= 100
if (cache.find(key)!=cache.end())
return cache[key];
int low=1,high=N;
while(low+1highValue){
high=middle;
}
else
low=high=middle;
}
int minimum = 1 + min(
max(superEggDrop(K - 1, low - 1), superEggDrop(K, N - low)),
max(superEggDrop(K - 1, high - 1), superEggDrop(K, N - high)));
cache[key]=minimum;
return cache[key];
}
};
在while循环中,我们利用了上文中提到的T1和T2的单调性,计算出了它们内部分别的最大值,因为在while循环之后我们是要先取最大值,然后在众多的最大值中取最小值,所以while内部是通过二分查找的思想找到最大值。这个版本的空间复杂度依然是O(KN),但是因为利用到了二分查找,所以其时间复杂度就降到了O(KNlogN),这在很多的算法中,已经是一个可以接受的时间复杂度了,只是并不是最优雅的而已。
更快的方法
这个方法是上一个方法的延续,并把时间复杂度从O(KNlogN)降到了O(KN),下面我们看一下它的思路。
首先令Xa = opt(K,N)是能够找最小移动次数的最小的X,根据上一个方法中我们分析T1和T2的单调性的方法,我们可以再次分析,并可以最终得出opt(K,N)是随着N的增长而增长的,这个我们也可以从下图中看到
随着N的增长,T2在向上移动,他们的交叉点Xa也在向上移动,那么在上一个方法中需要遍历从1到X的循环就可以改成从Xa到X了,因为小于Xa的都找不到最小移动次数。
与上一个方法自顶向下的方法不同,这次的解法是自底向上的,它每次的计算都是会先找到Xa,然后就可以直接计算出结果。
class Solution {
public:
int superEggDrop(int K, int N) {
vector dp(N+1);
for (int i = 0; i <= N; ++i) {
dp[i] = i;
}
// two and more eggs
for (int k = 2; k <= K; ++k) {
vector dp2(N + 1);
int x = 1;//start from floor 1
for (int n = 1; n <= N; ++n) {
while (x < n && (max(dp[x - 1], dp2[n - x]) > max(dp[x], dp2[n - x - 1]))) {
x++;
}
dp2[n] = 1 + max(dp[x - 1], dp2[n - x]);
}
for (int i = 0; i <= N; i++) {
dp[i] = dp2[i];
}
}
return dp[N];
}
};
这里需要特别注意一下dp,在for循环中,它代表是上一次循环解出来的最小值,也就是比当前楼层低一层的情况下的最优解。所以while条件中的max(dp[x - 1], dp2[n - x]) > max(dp[x], dp2[n - x - 1]),
带入T1 =dp(K−1,X−1),T2 =dp(K,N−X),就会发现其实是max(T1(x-1), T2(x-1)) > max(T1(x), T2(x))( ?)。
换个思路
上面的方法的思路,都还是顺着题目的思路的进行的,其实我们可以换一个思路来想:“求k个鸡蛋在m步内可以测出多少层”。我们令dp[k][m]表示k个鸡蛋在m步内可以测出的最多的层数,那么当我们在第X层扔鸡蛋的时候,就有两种情况:
- 鸡蛋碎了,我们少了一颗鸡蛋,也用掉了一步,此时测出
N - X + dp[k-1][m-1]层,X和它上面的N-X层已经通过这次扔鸡蛋确定大于F; - 鸡蛋没碎,鸡蛋的数量没有变,但是用掉了一步,剩余
X + dp[k][m-1],X层及其以下已经通过这次扔鸡蛋确定不会大于F;
也就是说,我们每一次扔鸡蛋,不仅仅确定了下一次扔鸡蛋的楼层的方向,也确定了另一半楼层与F的大小关系,所以在下面的关键代码中,使用的不再是max,而是加法(这里是重点)。评论里有人问到为什么是相加,其实这里有一个惯性思维的误区,上面的诸多解法中,往往求max的思路是“两种方式中较大的那一个结果”,其实这里的相加,不是鸡蛋碎了和没碎两种情况的相加,而是“本次扔之后可能测出来的层数 + 本次扔之前已经测出来的层数”。
class Solution {
public int superEggDrop(int K, int N) {
int[][] dp = new int[K + 1][N + 1];
for (int m = 1; m <= N; m++) {
dp[0][m] = 0; // zero egg
for (int k = 1; k <= K; k++) {
dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1;
if (dp[k][m] >= N) {
return m;
}
}
}
return N;
}
}
这个算法的空间复杂度没有啥疑问,就是O(KN),关于时间复杂度,原文说是O(KlogN),但是说实话我还没完全搞懂为啥,因为在我看来两层循环一个K,一个N,应该是O(KN)才对呀,如果有人知道这个是什么回事,还麻烦赐教下了。