算法通关村第十一关白银挑战——位运算符的高频算法题
大家好,我是怒码少年小码。
今天讲讲几个位运算的经典算法。
位移的妙用
1. 位1的个数
LeetCode 191:编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1’ 的个数。
- 输入:n = 00000000000000000000000000001011
- 输出:3
- 解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 ‘1’。
方法一
还记得我们上一篇()最后写的位运算代码套路的获取吗?与运算的特点是只有两边都为1结果才为1,否则结果为零。利用这个特点我们可以解决这个问题,例如数字3和数字1的二进制串进行与运算:
00000000000000000000000000001011
& 00000000000000000000000000000001
= 00000000000000000000000000000001
只用我们把1左移或者把原始数字右移然后进行与运算,结果为1说明这一位上是1,就记录“1”的数量加1,知道把32为都比较完后,有多少个记录就可以了。原始数字右移的代码如下:
int hammingWeight(int n) {
int count = 0;
for (int i = 0; i < 32; i++) {
count += (n >> i) & 1;
}
return count;
}
方法二:
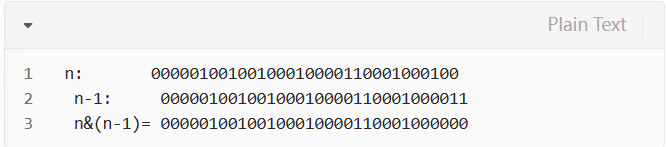
按位与运算有个性质:对于整数n,计算n & (n-1)的结果为将n的二进制表示的最后一个1变成0。利用这条性质,令n = n & (n-1),则n最后的二进制表示中的1数量减少一个。例如:
重复该操作,直到n的二进制表示中的全部数位都变成0,则操作次数即为n的位1的个数。代码如下:
int hammingWeight01(int n) {
int count = 0;
while (n != 0) {
n = n & (n - 1);
count++;
}
return count;
}
这两种方法,第一种的循环次数取决于原始数字的位数,第二种取决于原始数字种"1"的个数,效率自然高不少。
###2. 比特位计数
LeetCode 338:给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
- 输入:n = 2
- 输出:[0,1,1]
- 解释:
0 --> 0
1 --> 1
2 --> 10
自己先思考一下这题真的很简单!!
分析:遍历0 <= i <= n中的每一个数字,获取它们二进制串中的“1”的个数(可以单独设置一个函数),然后把个数保存到数组对应的位置上。
int helper(int n){
int count = 0;
while(n != 0){
n = n & (n-1);
count++;
}
return count;
}
vector<int> countBits(int n) {
vector<int> ans(n+1);
for(int i =0; i < n+1; i++){
int count = helper(i);
ans[i] = count;
}
return ans;
}
这就是一通百通吧。
3. 颠倒无符号整数
LeetCode 190:颠倒给定的 32 位无符号整数的二进制位。
分析:肯定是先要获取某一位,然后再把它放到应该的位置上去。获取就用原始数字与1进行与运算,然后原始数字右移,这样我们就能得到低位置上的二进制数,然后通过左移power个来放到高位
int reverseBits(int n) {
int reversed = 0, power = 31;
while (n != 0) {
reversed += (n & 1) << power;
n >>=1;
power--;
}
return reversed;
}
n >>= 1是一个右移操作符,它将变量n的值向右移动一位。类似于n+=1是把n的值加一。
位实现加减乘除专题
在计算机中,位运算的效率比单纯加减乘除的效率更高,因此在高性能软件的源码中大量应用。
1. 位运算实现加法
LeetCode 371:给你两个整数 a 和 b ,不使用 运算符 + 和 - ,计算并返回两整数之和。
两个位加的时候,需要考虑两个问题:进位部分是什么?不进位部分是什么?
- 对于不进位部分(0+0,1+0,0+1)的情况是:相同为0,不同为1(其实是a⊕b)
- 对于进位部分(1+1),a和b的这一位都是1的时候才会进位,而且进位只能是1(其实是a&b=1),然后位数由1位变成两位,需要手动移位(a & b) << 1
所以:
- 不进位部分:用a⊕b计算就可以
- 是否进位,以及进位值使用(a & b) << 1计算即可
int getSum(int a, int b) {
while (b != 0) {
int sign = (a & b) << 1;//计算出哪些位同时为1(这些需要进位)
a = a ^ b; //无进位和
b = sign;
}
return a;
}
从低位开始,处理每一位,考虑进位,并逐步向高位移动。
2. 递归乘法
LeetCode 08.05:递归乘法。 写一个递归函数,不使用 * 运算符, 实现两个正整数的相乘。可以使用加号、减号、位移,但要吝啬一些。
示例:
- 输入: a=1,b=10
- 输出:10
不用*计算,一种方法是将一个作为循环的参数,对另一个进行累加,但是这样效率太低,所以还要考虑位运算。
首先,需要求得a和b的最小值和最大值,把其中的最小值当做乘数(选最小值当乘数,后续计算算的少),将其拆分成2的幂的和(方便左移),
即min = a0 * 2^0 + a12^1 + a2 2^2 + … + ai2i+…,其中ai取0或者1,相当于用二进制的视角去看待min,比如12用二进制来表示就是1100,即1000+0100
13 * 12 = 13 * (8+4)= 138 + 13*4 = (13<<3)+(13<<2);
上面仍然需要左移5次,存在重复计算,可以进一步简化:
假设我们需要的结果是ans
定义临时变量 :tmp = 13<<2 = 52计算后,可以先让ans = 52
然后tmp继续左移一次tmp = 52<<1 = 104,此时再让ans = ans + tmp
此时只要执行三次移位和一次加法
int multiply(int a, int b) {
int min = a < b ? a : b;
int max = a > b ? a : b;
int ans = 0;
for (int i = 0; min != 0; i++) {
if ((min & 1) == 1) {
ans += max;
}
min >>= 1;
max += max;
}
return ans;
}
END
本文的主要内容来自算法通关村。