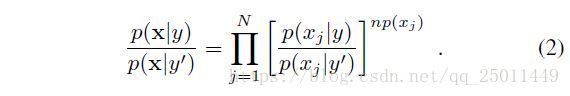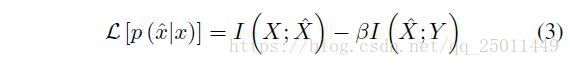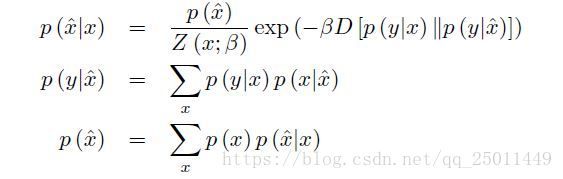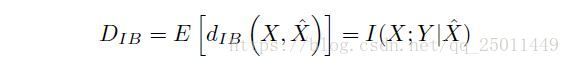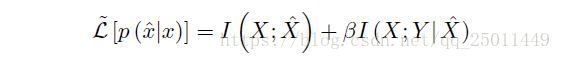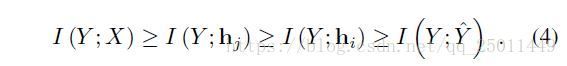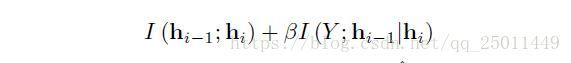【论文精读】Deep Learning and the Information Bottleneck Principle

Deep Learning and the Information Bottleneck Principle

原文链接：Deep Learning and the Information Bottleneck Principle

上次读了《Deep Learning under Privileged Information Using Heteroscedastic Dropout》这篇文章，里面提到了信息瓶颈（Information Bottleneck）这个概念，据说这是能揭示深度学习原理的一个想法，所以这次找来了深度学习IB理论的开山之作，由Tishby写的这篇文章拜读一下，本人水平有限，有些理论上不能理解，望各位大佬见谅和指教。

大家也可以参考一下B站UP主深度碎片的系列视频中对这篇文章的解读，也可以看一下这篇博文中的评述。

Abstract

利用信息瓶颈原理的理论框架对神经网络进行了深入分析。这篇文章首先展示了任何DNN都可以通过隐层与输入和输出变量之间的共享信息（mutual information）来量化。利用这种表示方法，可以计算出DNN的最优信息理理论极限，得到有限样本泛化边界。接近理论极限的优势可以体现在泛化边界和网络的简易程度。作者认为，最优体系结构、每个层的层数和每个层的特征/连接数都与信息瓶颈权衡的分叉点有关，即输入层相对于输出层的相关压缩。层状网络的层次化表示自然对应于信息曲线上的结构相变（应该就是信息保留程度随着网络层级的变化）。这种新的见解能够带来新的最优边界和深度学习算法。

I. Introduction

深度学习在监督学习中表现优异，但其原理方面的研究还很少。Metha和Schwab的论文提出当隐层接近RG fixed point的时候，各层之间的特征在统计上变得越来越不相关。由此受到启发，根据信息瓶颈原理，作者提出深度学习的目标就是在学习的过程中最大化地压缩输入信息，最大化地保留输出信息。

应用了信息瓶颈理论，DNNs的层级结构可以生成一个连续的Markov链，这个Markov链可以近似地表示出所有的关系和数据。这样的话网络上每一层都可以被保留的输入信息、输出信息和预测信息来量化。这样的Markov链和数据处理的不对等可以更有效地检验隐层的表示效率。它还为我们提供了压缩/预测问题的信息理论极限，并从理论上量化了给定训练数据下提出的每个DNN。此外，利用已知的IB上的有限样本边界，DNNs的这种表示给出了一个新的理论样本复杂度界。

这里作者说，在给定输出分类的条件下，只有当输入单元是有条件的独立的时候线性可分才是有可能的。这种不可分性是由于IB曲线上representational phase transition (bifurcation)和数据二级依赖性造成的（不懂啥意思）。所以作者提出了一些新的信息理论优化条件、采样复杂度边界和DNN的设计原则。

文章的剩余部分组织结构如下：首先将DNNs看作一个看成各个层之间的一个Markov级联；接着将DNNs当作特殊的rate-distortion distortion plane结合IB理论来研究；第三部分应用一个新的优化学习理论有限采样边界到IB问题，当作信息理论约束来研究DNNs；最后介绍一个IB结构phase transitions和DNNs层级结构之间有趣的联系。

II. Background

A. Deep Neural Networks

DNNs善于使用层级的处理从维度很高的输入数据中提炼出与输出直接相关的信息。目前DNNs的训练用到了随机的一些算法，比如SGD和RBM中的随机映射，但还不清楚为什么和在什么时候使用随机的技巧有用。在CNNs中数据的对称性也通过权值共享被考虑进来。

然后作者从理论上解释了为什么只有当输入数据是条件独立的，它们才是线性可分的。根据贝叶斯定理：

上面式子经过化简可以变成贝叶斯定理的一般形式，为什么要这样写呢，这样写是为了方便与sigmoid激活函数形式类似，其中：

很容易想到如果 wj=logp(xj|y)p(xj|y′) w j = l o g p ( x j | y ) p ( x j | y ′ ) ， b=logyy′ b = l o g y y ′ ，同时满足 hj=np(xj) h j = n p ( x j ) ，那么贝叶斯公式就完全变成了神经元的激活函数。但是这种条件独立在一般的输入数据中很难实现。

对于基于DNN结构的RBM可以通过连续RG变换来实现近似的条件独立，但对于其他的DNN没有一般的方法来实现，在这篇文章中，作者提出了一种纯粹的信息理论观点，该观点可以量化它们的性能，为它们的效率提供理论限制，并为它们的泛化能力提供新的有限样本复杂度边界。此外，分析表明，最优的DNN体系结构也仅仅是由数据联合分布的信息理论分析所决定的。

B. The Information Bottleneck Principle

IB被用来作为从输入 X∈X X ∈ X 中提取输出 Y∈Y Y ∈ Y 的相关信息的准则，他们之间相关的信息可以被定义为共享信息 I(X,Y) I ( X , Y ) 。最优的输入可以捕获到所有与输出相关的信息，并且摒弃掉所有与输出不相关的部分。

输入 X X 中与输出Y Y 相关的部分可以用 X^ X ^ 表示， X^ X ^ 是能够代表 Y Y 的minimal sufficient statistics。也就是说，它是能都获取到I(X;Y) I ( X ; Y ) 的 X X 的最简单的映射。因此，为了找到X^ X ^ ，要使得 I(X;X^) I ( X ; X ^ ) 尽量小（就是说让 X^ X ^ 尽量简单），并且 I(X^;Y) I ( X ^ ; Y ) 尽量大（就是说让 X^ X ^ 尽量抓住与输出的相关信息）。那么可以构造Lagrange方程如下：

对于一般的分布 p(X,Y) p ( X , Y ) 来说，准确的minimal sufficient statistics或许并不存在，在预测时的Markov链也不成立。如果令 Y^ Y ^ 作为预测变量，根据DPI，那么 I(X;Y)≥I(Y;Y^) I ( X ; Y ) ≥ I ( Y ; Y ^ ) ，当且仅当 X^ X ^ 是一个充分代表 Y Y 的数据的时候等号成立。

根据文献要满足以下等式IB问题才有最优解：

上面的IB问题可以看作是一个rate-distortion问题，然后作者定义了：

这是在计算KL散度，我觉得可以理解为两个分布之间的偏差，它的期望：

上式就代表着两个分布之间的偏差的期望，并将其定义为I(X;Y|X^) I ( X ; Y | X ^ ) ，当然我们希望这个期望越小越好，所以IB的拉格朗日公式可以写成：

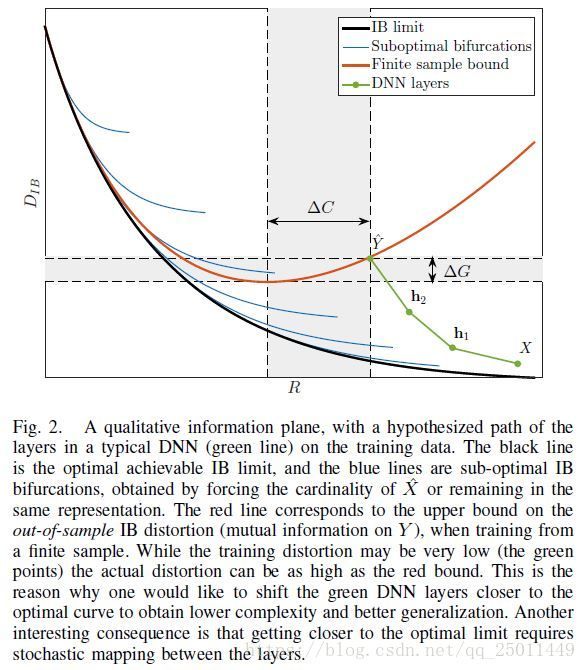
下面的部分作者开始介绍图2，这部分不太懂，大致是在说由拉格朗日方程得到的IB曲线在不同的 β β 下会产生不同的 X^ X ^ ，最优的情况就是能够学到最为minimal sufficient的 X^ X ^ ，同时网络结构也能最为精简。（要理解这一部分的内容，应该再看一看rate-distortion的文献）

III. A NEW INFORMATION THEORETIC LEARNING PRINCIPLE FOR DNNs

A. Information characteristics of the layers

之前第II节中用信息理论分析了Markov链中神经网络输入和输出的联系，这里讨论了每一层的联系，类似地，可以用以下不等式表示：

同样，对于神经网络中的每一层而言都要最大化 I(Y;hi) I ( Y ; h i ) 同时最小化 I(hi−1;hi) I ( h i − 1 ; h i ) 。之前提到的 I(X^;Y) I ( X ^ ; Y ) 在这里对应着 I(Y;hi) I ( Y ; h i ) 可以有效地约束预测的误差（这个值越大，说明网络与输出的共享信息越多，预测越准确），同时 I(Y;Y^) I ( Y ; Y ^ ) 可以用来衡量DNN的好坏。这样IB原则中的信息扭曲也可以来衡量每个隐层甚至每个神经元的表现，根据下面的拉格朗日方程：

Finite Samples and Generalization Bounds

这一小节的前半部分不太理解，后面讲了作者定义的两个概念，一个叫做泛化间隔（generalization gap，指的是确定了输出中本应该被捕获但却未被捕获的信息量），一个叫做复杂度间隔（complexity gap，确定了网络中不必要的复杂度），然后以这IB套理论做指导，可以找到更好的网络。

IV. IB PHASE TRANSITIONS AND THE BREAKDOWN OF LINEAR SEPARABILITY

这里讨论了IB的曲线跟之前说过的那个可分割性之间的联系，这里还得再研究一下。

Conclusion

作者总结了以上工作，指出了这篇文章所提出的理论的几点优势：

1. 通过估计每个隐层和输入输出变量站之间的共享信息，整个网络和他的隐层可以在information plane上直接得到最优的IB limit。
2. 一个新的基于信息理论的DNN的最优化准则。
3. 使用IB有限采样边界的网络泛化能力上的采样复杂度边界。
4. 随机DNN架构可以与最优的理论限制更接近。
5. 网络架构，隐层的数量和结构，IB问题中的phase transitions之间存在着联系都和在关键点上数据的二阶相关性有关。