详解二叉树之堆
文章目录
-
- •知识回顾
- • 知识点一：二叉树的存储结构
-
- • 1. 二叉树的顺序结构
- • 2. 二叉树的链式结构
- • 知识点二：堆的概念及结构
-
- • 1. 二叉树和堆
- • 2. 堆的概念及结构
-
- •2.1 堆的概念
- •2.2 堆的结构
- •2.3 堆的性质
- • 3. 堆调整算法
-
- •3.1 小根堆向下调整算法
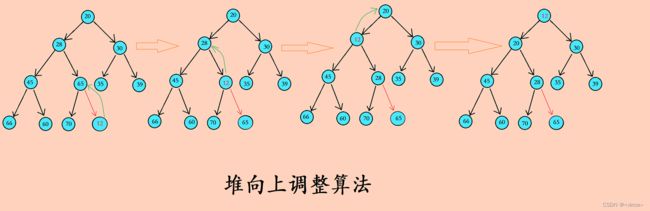
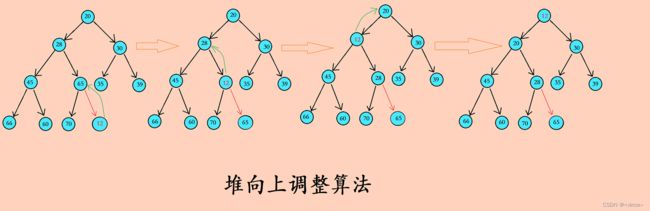
- •3.1 小根堆向上调整算法
- • 4. 堆的实现
-
- •4.1 堆的初始化
- •4.2 堆的销毁
- •4.3 堆的插入
- •4.4 堆的删除
- •4.5 堆的判空
- •4.6 返回堆顶数据
- •4.7 统计堆内数据个数
- •4.8 打印堆内数据
- •4.9 头文件
- •4.10 主函数源文件
- • 知识点三：堆的应用
-
- • 1. 堆排序
- • 2. TOP-K问题
- •vince 结语
•知识回顾
大家好啊！我是vince，我们继续进入纯C实现数据结构的坑里来，上一篇文章 vince 详解了树的概念和结构，里面包含了树和二叉树的相关术语及其概念，相对来说是比较好理解的~
vnce今天给大家带来二叉树的堆结构实现，这里的堆学习为后面的堆排序打基础。☀️也希望 vince 的总结在方便后面复习的同时也能给大家带来帮助。
当然在大家看这篇文章之前，vince 还是建议大家先复习复习前面的顺序表和链表，毕竟这里堆的实现以及后面树链式结构的学习也与他们息息相关。
知识连线时刻（直接点击即可）
复习回顾
详解顺序表
详解双向带头循环链表
学习数据结构当然离不开大量操作练习，因此在这里 给爱学习的小伙伴们推荐个学习、刷题的网站——牛客网，其中面试题应有尽有，真的能够给你带来很好的学习体验。
爱学习的亲们！请点击我开始注册！学习、刷题
我们先来看看今天学习的思维导图（主要是顺序结构中的堆）
• 知识点一：二叉树的存储结构
二叉树一般可以使用两种结构存储，一种是顺序结构，一种是链式结构。
• 1. 二叉树的顺序结构
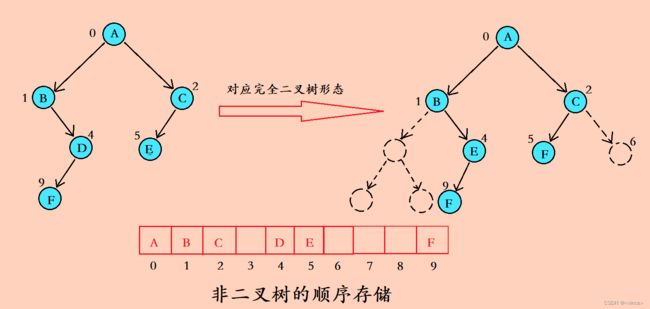
顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树， 因为不是完全二叉树会有空间的浪费。而现实使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。
图解完全二叉树的顺序存储：
图解非完全二叉树的顺序存储：
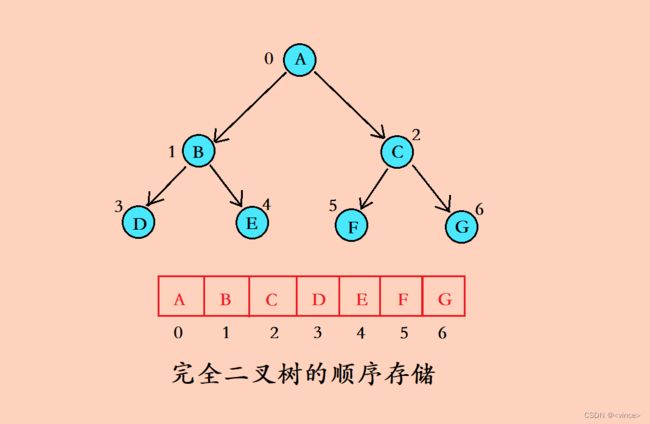
文字分析：
非完全二叉树利用顺序结构来存储，在上图中你就会发现有空间浪费现象。因此，一般只有完全二叉树即堆拿顺序结构存储。
• 2. 二叉树的链式结构
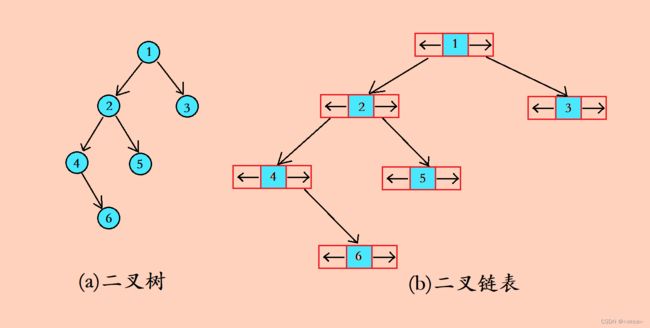
二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链，当前我们介绍学习一般都是二叉链，后面学到高阶数据结构如红黑树等会用到三叉链。
图解分析：
二叉链代码示例：
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{
struct BinTreeNode* _pLeft; // 指向当前节点左孩子
struct BinTreeNode* _pRight; // 指向当前节点右孩子
BTDataType _data; // 当前节点值域
}
二叉链图解分析：
三叉链代码示例：
typedef int BTDataType;
// 三叉链
struct BinaryTreeNode
{
struct BinTreeNode* _pParent; // 指向当前节点的双亲
struct BinTreeNode* _pLeft; // 指向当前节点左孩子
struct BinTreeNode* _pRight; // 指向当前节点右孩子
BTDataType _data; // 当前节点值域
}；
• 知识点二：堆的概念及结构
• 1. 二叉树和堆
普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常对堆(一种二叉树)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。 这里数据结构中的堆和操作系统中的堆是两个概念，前面还介绍学习过数据结构中的栈和内存中的栈两个概念也不同哈~
• 2. 堆的概念及结构
•2.1 堆的概念
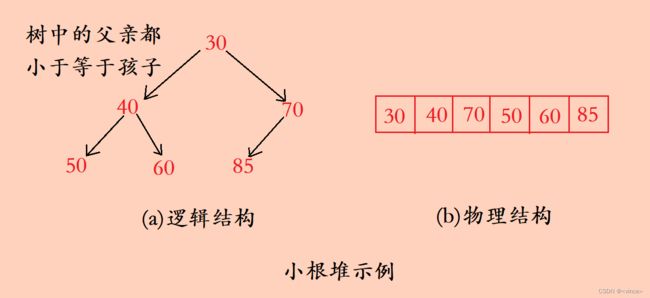
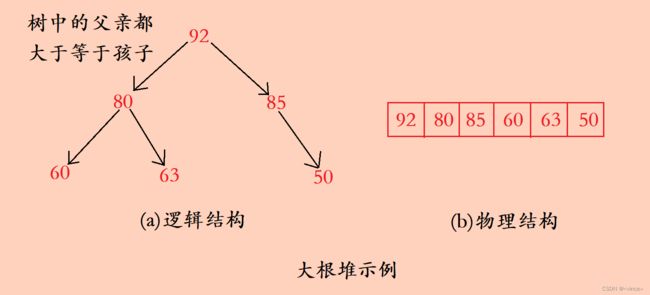
如果有一个关键码的集合k = { k 0 k_{0} k0， k 1 k_{1} k1， k 2 k_{2} k2，…， k ( n − 1 ) k_{(n-1)} k(n−1)}，把所有元素按完全二叉树的顺序存储方式存储在一个数组中，并且满足： k i k_{i} ki <= k 2 ∗ i + 1 k_{2*i+1} k2∗i+1 且 k i k_{i} ki <= k 2 ∗ i + 2 k_{2*i+2} k2∗i+2（或 k i k_{i} ki >= k 2 ∗ i + 1 k_{2*i+1} k2∗i+1 且 k i k_{i} ki <= k 2 ∗ i + 2 k_{2*i+2} k2∗i+2），i = 0, 1 , 2……则称为小堆（或大堆）。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。
•2.2 堆的结构
小根堆结构图解分析：（树中的父亲都小于孩子）
大根堆结构图解分析：（树中的父亲都大于孩子）
•2.3 堆的性质
堆中某个节点的值总是不大于或不小于其父节点的值；
堆总是一棵完全二叉树。（堆和二叉树的关系）
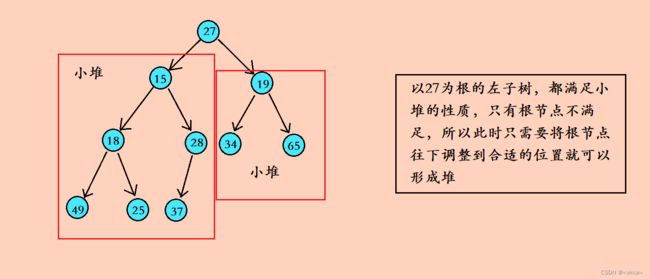
• 3. 堆调整算法
•3.1 小根堆向下调整算法
小根堆向下调整过程图解：
•3.1 小根堆向上调整算法
小根堆向上调整过程
• 4. 堆的实现
这里拿实现小根堆来举例详解。
•4.1 堆的初始化
//堆的初始化
void HeapInit(HP* php)
{
assert(php);
php->a = NULL;
php->size = php->capacity = 0;
}
文字分析：
这里的结构还是和之前学过的顺序表结构类似，因此前面也希望大家去复习一下前面的顺序表结构，这样这里就能够很容易理解。
•4.2 堆的销毁
//堆的销毁
void HeapDestory(HP* php)
{
assert(php);
free(php->a);
php->a = NULL;
php->size = php->capacity = 0;
}
•4.3 堆的插入
堆的插入，不只是插入数据，还要使得插入数据后整体依然保持为堆。因此，此时就需要用到调整算法，这里是建小根堆，在数据插入这里需要用到向下调整算法。
//交换函数
void Swp(HPDataType* p1, HPDataType* p2)
{
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
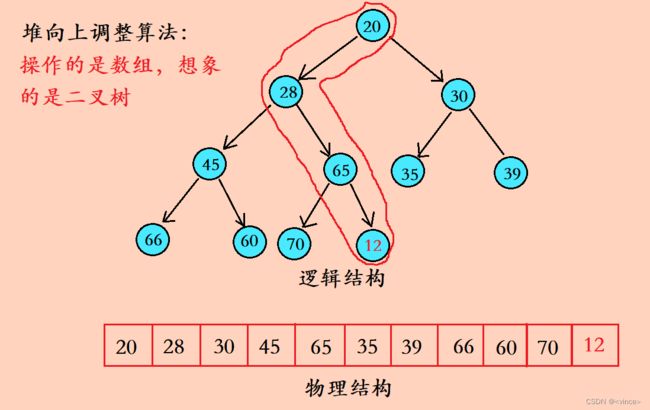
//小堆向上调整算法
//这里算法逻辑思想是二叉树，物理上实际操作的是数组中的数据
void Adjuestup(HPDataType* a, size_t Child)
{
size_t Parent = (Child - 1) / 2;
while (Child > 0)
{
if (a[Child] < a[Parent])//这里条件是Child < Parent 值时交换实现的是小根堆，大于的时候交换实现的是大根堆
{
Swp(&a[Child], &a[Parent]);
Parent = (Child - 1) / 2;
}
else
{
break;
}
}
}
//堆的插入 O(logN)
void HeapPush(HP* php, HPDataType x)
{
assert(php);
if (php->size == php->capacity)
{
size_t newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
else
{
php->a = tmp;
php->capacity = newcapacity;
}
}
php->a[php->size] = x;
php->size++;
//以上实在数组尾部插入数据，插入完成后，
//还需要通过算法调整，保证让其还是堆
//以下就是堆的向上调整算法
Adjuestup(php->a, php->size - 1);
}
文字分析：
这里是对小堆进行数据插入，用到了向上调整算法，算法逻辑思想是二叉树，物理上实际操作的是数组中的数据。因为插入一个数据之后，可能整体结构就被破坏，所以这里利用向上调整法是为了每插入一个数据后，将整体进行调整使其依然保持一个堆的结构。
图解分析：
•4.4 堆的删除
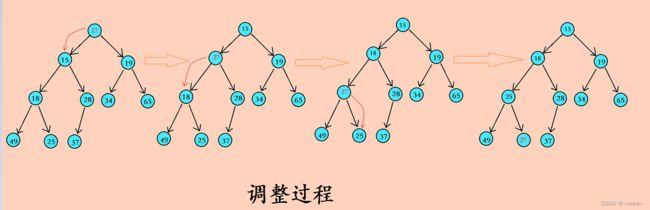
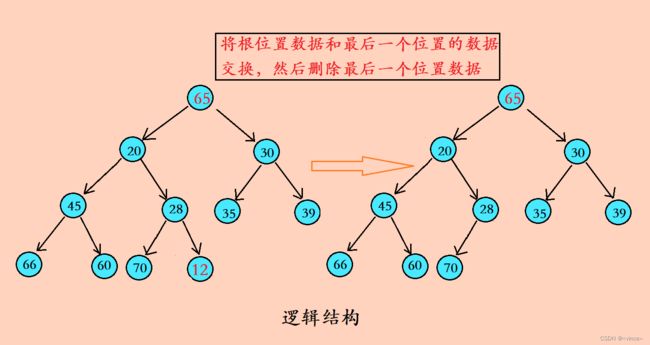
堆的删除这里有一种更优的方法：将第一个位置的数和最后一个位置的数交换，然后删除最后一个位置的数，最后进行向下调整。这里就用到了向下调整算法，向下调整的目的还是让其保持成一个堆的结构。
//向下调整算法
void AdjuestDown(HPDataType* a, size_t size, size_t root)
{
size_t Parent = root;
size_t LeftChild = Parent * 2 + 1;//计算该parent的左孩子
while (LeftChild < size)
{
//这种方法是保证一直指向左孩子，避免右孩子不存在而出现越界情况
//LeftChild + 1 即指向右孩子
if (LeftChild + 1 < size && a[LeftChild + 1] < a[LeftChild])//如果这里和下面 < 换成 >
//则是大根堆的向下调整算法
{
++LeftChild;//得到右孩子
}
if (a[LeftChild] < a[Parent])
{
Swp(&a[LeftChild], &a[Parent]);
Parent = LeftChild;
LeftChild = Parent * 2 + 1;//始终都指向左孩子
}
else
{
break;
}
}
}
//删除堆顶元素
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);//size大于0才能进行删除
Swp(&php->a[0], &php->a[php->size - 1]);//将根位置数据与最后一个位置数据交换
--php->size;
//利用向下调整算法进行调整
AdjuestDown(php->a,php->size,0);
}
文字分析：
堆的删除这里利用了一种最优的方法，就是第一个数和最后一个数交换后，删除最后一个数，然后利用向下调整算法进行调整。向下调整算法过程：找出左右孩子中较小的那个然后跟父亲进行比较，如果比父亲小就进行交换，依次向下比较调整。这里实际删除的是原来根位置的数据，即删除堆顶数据。
图解分析：
•4.5 堆的判空
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
•4.6 返回堆顶数据
HPDataType HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);//size大于0，才能获取到
return php->a[0];
}
•4.7 统计堆内数据个数
//计算堆内数据个数
size_t HeapSize(HP* php)
{
assert(php);
return php->size;
}
•4.8 打印堆内数据
//打印堆内数据
void HeapPrint(HP* php)
{
assert(php);
for (int i = 0; i < php->size; i++)
{
printf("%d ", php->a[i]);
}
printf("\n");
}
•4.9 头文件
#include •4.10 主函数源文件
简单举例测试一下：
#include "Heap.h"
void TestHeap1(HP* hp)
{
HeapInit(hp);
HeapPush(hp, 2);
HeapPush(hp, 9);
HeapPush(hp, 3);
HeapPush(hp, 0);
HeapPush(hp, 7);
HeapPush(hp, 10);
HeapPrint(hp);
HeapDestory(hp);
}
int main()
{
HP h;
TestHeap1(&h);
return 0;
}
运行结果：
• 知识点三：堆的应用
• 1. 堆排序
//玩一个堆排序（升序）O(N*logN)
void HeapSort(HPDataType* a,size_t size)
{
assert(a);
HP H;
HeapInit(&H);//初始化
for (size_t i = 0; i < size; i++)
{
HeapPush(&H, a[i]);//将数据插入堆中
}
size_t j = 0;
while( !HeapEmpty(&H))
{
a[j++] = HeapTop(&H);//这里是小根堆，因此将堆顶数据依次放入数组中，就是先从小到大排序
HeapPop(&H);//结束后再将堆数据删除
}
HeapDestory(&H);//最终销毁堆
}
int main()
{
int a[] = { 4, 2, 3, 0 , 1, 6, 9, 7 };
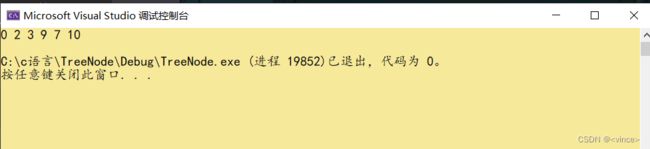
HeapSort(a, sizeof(a) / sizeof(a[0]));
for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
printf("%d ", a[i]);
}
printf("\n");
return 0;
}
文字分析：
这里的堆排序实际上是因为建立的小根堆，所以堆顶位置的数据一定是堆内最小的数据，因此每次取出当前的堆顶数据，然后再删除堆顶数据，此时就会再得到一个次小的数据放在堆顶，就这样依次取出，就能得到一个升序的数组，从而达到数据进行升序排序。堆排序属于一个选择排序。时间复杂度：O(N*logN)
运行结果：
• 2. TOP-K问题
TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：
1.用数据集合中前K个元素来建堆：前k个最大的元素，则建小堆；前k个最小的元素，则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
时间复杂度：O(K+logk*(N-K)
空间复杂度：O(K)
如果N非常大，K非常小，那基本上就是O(N)
举例如下：
void PrintTopK(int* a, int n, int k)
{
//1.建堆--用a中前K个元素建堆
int* KminHeap = (int*)malloc(sizeof(int) * k);
assert(a);
assert(KminHeap);
for (int i = 0; i < k; ++i)
{
KminHeap[i] = a[i];
}
//建小堆 （注意这里利用向下调整法调整建立小根堆）
for (int j = (k - 1 - 1) / 2; j >= 0; --j)
{
AdjuestDown(a, k, j);
}
//2.将剩余n-k个元素一次与堆顶元素进行比较
for (int i = k; i < n; ++i)
{
if (a[i] > KminHeap[0])
{
KminHeap[0] = a[i];
AdjuestDown(KminHeap, k, 0);
}
}
for (int j = 0; j < k; j++)
{
printf("%d\n", KminHeap[j]);
}
printf("\n");
free(KminHeap);
}
void TestTopK()
{
int n = 10000;
int* a = (int*)malloc(sizeof(int) * n);
assert(a);
srand(time(0));
for (int i = 0; i < n; ++i)
{
a[i] = rand() % 1000000;
}
a[24] = 1000000 + 1;
a[12] = 1000000 + 2;
a[51] = 1000000 + 3;
a[511] = 1000000 + 4;
a[115] = 1000000 + 5;
a[2331] = 1000000 + 6;
a[9999] = 1000000 + 7;
a[766] = 1000000 + 8;
a[4235] = 1000000 + 9;
a[316] = 1000000 + 10;
PrintTopK(a, n, 10);
}
运行结果：
•vince 结语
二叉树和堆的相关概念和结构的介绍和学习到这里就结束啦~但是数据结构的学习之路远没有结束哈！这是非线性结构的开端，后面还有大力输出学习非线性结构。但是在这里，希望大家能够将前面的树的基础概念以及之前的线性结构知识进行回顾复习，使整个纯C数据结构学习是连贯的，这样更加利于我们的学习和理解以及继续拓展。
如果各位大佬们觉得有一定帮助的话，就来个赞和收藏吧，如有不足之处也请批评指正。
学习数据结构当然离不开大量操作练习，因此在这里 给爱学习的小伙伴们推荐个学习、刷题的网站——牛客网，其中面试题应有尽有，真的能够给你带来很好的学习体验。
爱学习的亲们！请点击我开始注册！学习、刷题
代码不负有心人，98加满，向前冲啊
以上代码均可运行，所用编译环境为 vs2019 ,运行时注意加上编译头文件#define _CRT_SECURE_NO_WARNINGS 1