并查集

一、并查集定义

1. 并查集是一种树型的数据结构，用于处理一些不相交集合（disjoint sets）的合并及查询问题。
2. 并查集通常包含两种操作

• 查找(Find)：查询两个元素是否在同一个集合中
• 合并(Union)：把两个不相交的集合合并为一个集合

注意：双亲结点就是父结点

二、并查集思想

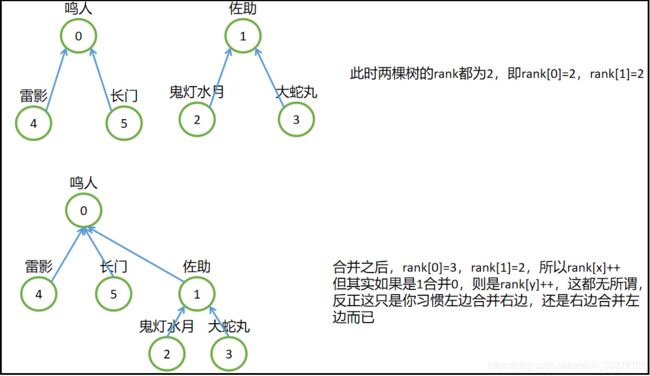
如图现在大陆上有下面六位鼎鼎大名的忍者，且各自为王！

      奈何鸣人用嘴遁，轻而易举的让雷影和长门相信自己，所以就这样被鸣人收服了，以后就跟着鸣人混日子了。（此时鸣人就是雷影和长门的老大，即雷影集合以及长门集合就被合并到鸣人集合中，并且鸣人为代表元素，即0号为代表元素）。佐助为了力量，直接秒杀了大蛇丸，并且释放鬼灯水月，让他跟着自己混日子，大蛇丸这个时候却不记仇，十分欣赏佐助，所以他们两个就跟随佐助，一起搞事情。（此时，大蛇丸集合以及鬼灯水月集合就被合并到佐助集合中，并且佐助为大蛇丸和鬼灯水月的代表，即1号为代表元素）现在的局势如下图所示：

      此时鬼灯水月看雷影不爽，想扇他一巴掌，奈何发现自己好像打不过，于是向自己的老大佐助求助，让他去KO雷影，结果刚劈了雷影一只手，雷影果断喊出自己的老大鸣人，只见鸣人一招螺旋丸再加一招嘴遁，顺利收服了佐助，让他成为村里的情报人员。此时两大阵营合并为一个阵营，即佐助集合被合并到鸣人集合：

三、并查集代码：

(1)初始化

#define MAXN 100
int Parent[MAXN];

void init(int n){
    for(int i=0;i<n;i++){
        Parent[i]=i;        //存放每个结点的结点（或双亲结点）
    }
}

现在每个结点各自为王，所以自己就是自己的老大，所以Parent数组指向的就是自己本身。

(2)查找

//查询根结点
int find(int x){
    if(Parent[x]==x)
        return x;
    else
        return find(Parent[x]);
}

      查找自己的老大是谁，用递归的方法实现对集合中的代表元素(老大)的查询：一层一层访问双亲结点，直至根结点（根结点的标志就是根结点本身）。要判断两个元素是否属于同一个集合，只需要看它们的根结点是否相同即可，即看他们的老大是否是同一个人。

例如查找鬼灯水月的老大是谁？

• 通过递归查找，先查找数组下标为2的元素，为1，所以他自己不是自己的老大，他的老大是1号，也就是佐助
• 接下来看看佐助的老大是谁，查看数组下标为1的元素，为0，所以佐助也不是自己的老大，佐助的老大是0号，也就是鸣人
• 接下来看看鸣人的老大是谁，查看数组下标为0的元素，为0，所以鸣人自己就是老大，所以递归结束，这个集合的老大为0号。

(3)合并

//合并,把 j 合并到 i 中去，就是把j的双亲结点设为i
void merge(int i,int j){
    Parent[find(j)] = find(i);
}

      例如，此时要合并结点3和结点5，并不是直接把他们两个合并，而是先查找到他们各自的老大是谁，结点3的老大是结点1，结点5的老大是结点0，然后结点1被结点0收服了，所以结点0成为了结点1的老大，此时就把结点1指向到结点0，即把数组下标为1的元素内容改为0。结果如下图所示：

注意：这里为什么一定是结点0打败结点1？其实这是随意的，不过我习惯左边的结点合并右边的结点而已。

四、路径压缩

用于提高并查集的效率

假设有这样的场景：

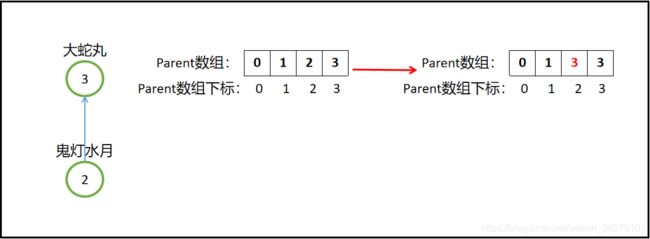
• 一开始大蛇丸直接KO鬼灯水月，收入麾下，即执行merge(3,2)操作，就是把集合2合并到集合3中，即parent[2]=3；

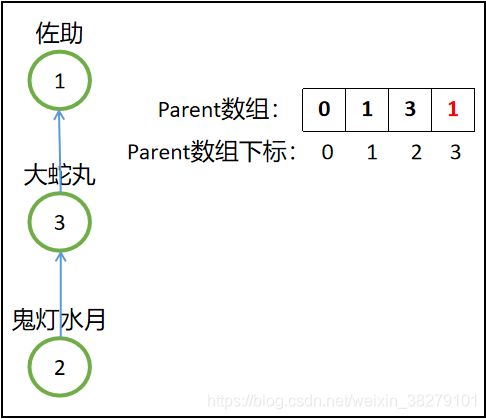
• 然后佐助想要收服鬼灯水月，但是得经过鬼灯水月的老大，大蛇丸的同意才行，无奈之下佐助一招千鸟秒杀了大蛇丸，从此鬼灯水月和大蛇丸就加入到佐助这个阵营了，即执行merge(1,2)，就是把2号合并到集合1中，于是先找到2号的老大，即3号，所以1号直接就收服3号，即parent[3]=1，这样一来集合3就被合并到集合1中去了;（注意，集合3代表了元素2和3）
  

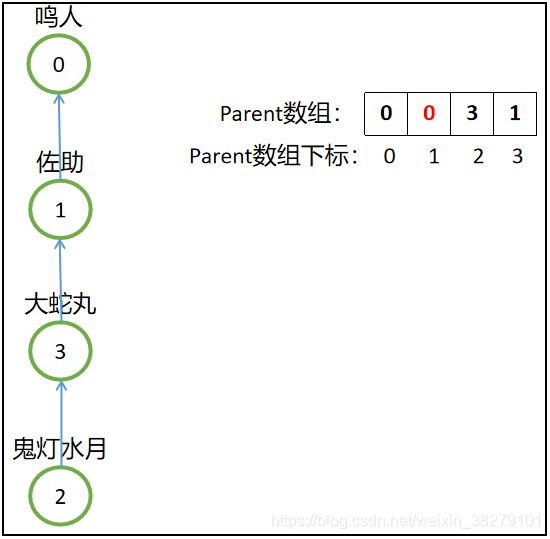
• 然后鸣人想要收服鬼灯水月，所以就得要一层一层往上找鬼灯水月的老大是谁，先是找到了大蛇丸，结果大蛇丸只是一个小队长，然后再往上找，发现真正的老大是佐助，所以就直接收服佐助，即执行merge(0,2)，从2找到3，再从3找到1，最后进行合并，parent[1]=0;
  

• 最后四个元素合并成上面这样一个大集合，但是这样就变成了一条长长的链，想要找到根结点（老大）是谁就变得越来越难，因为要一层一层的往上找才行，鸣人就不乐意了，鸣人希望他们每个人的直接上司就是自己，所以突发奇想，想到了路径压缩这一招！

• 既然判断两个元素是否是同一个集合看的是他们的根结点是否一样，那么还不如直接把每个元素的父结点改为这个集合的代表元素（即根结点），就像下图一样：
  
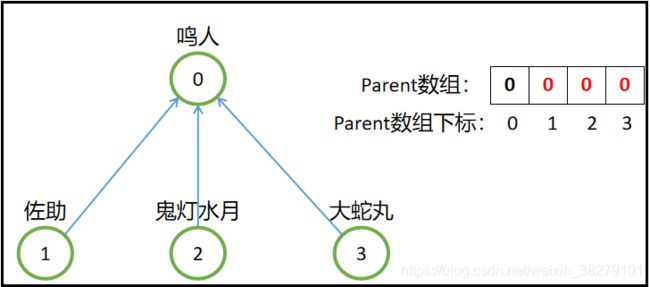
         这样一来就方便多了，就不用一层一层往上找自己的老大是谁了，就直接向上找一层就行了。那么应该要怎么实现呢？只要在查找的过程中，把沿途的每个双亲结点都设为根结点即可！下一次查找的时候就可以省去很多查找步骤了。

(1)查找代码：

//查询根结点
int find(int x){
    if(Parent[x]==x)
        return x;
    else{
            Parent[x]=find(Parent[x]);
            return Parent[x];
    }
}

查找代码通常简化为下面一行：

int find(int x)
{
    return x == Parent[x] ? x : (Parent[x] = find(Parent[x]));
}

(2)路径压缩完整代码：

#include 
using namespace std;

#define MAXN 100
int Parent[MAXN];

//初始化，现在各自为王，自己就是一个集合
void init(int n){
    for(int i=0;i<n;i++){
        Parent[i]=i;
    }
}

//查询根结点
int find(int x){
    if(Parent[x]==x)
        return x;
    else{
            Parent[x]=find(Parent[x]);   //顺便把双亲结点也设置为根结点，路径压缩
            return Parent[x];
    }
}

//合并,把 j 合并到 i 中去，就是把j的双亲结点设为i
void merge(int i,int j){
    Parent[find(j)] = find(i);
}

int main()
{
    return 0;
}

五、按秩合并

很多人有一个误解，就是认为并查集经过路径压缩优化之后，并查集是只有两层的一颗树，其实不是的。因为路径压缩只在查找的时候进行，也只压缩一条路径，所有并查集的最终结构仍然可能是比较复杂的。

(1)按秩合并的思想

       假设，我们现在有一颗比较复杂的树，需要和一个单个元素的集合进行合并，您认为要怎么合并？是左边合并右边，还是右边合并左边？

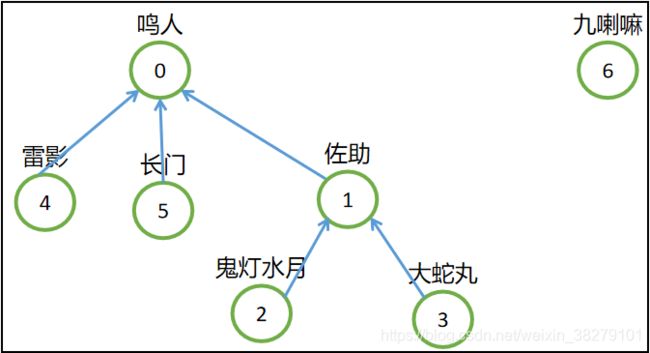
• 如果您选择九喇嘛收服了鸣人，即集合0合并到集合6中去，这样合并之后就会使树的深度加深，原来集合0中的树的每个元素到根结点的距离都变长了，之后我们寻找根结点的路径也就会相应变长，即使我们有路径压缩的方法，但是进行路径压缩之前还是会消耗时间；
• 如果选择鸣人收服九喇嘛，即集合6合并到集合0中去，则不会有这个问题，即树的深度不会增加。
  
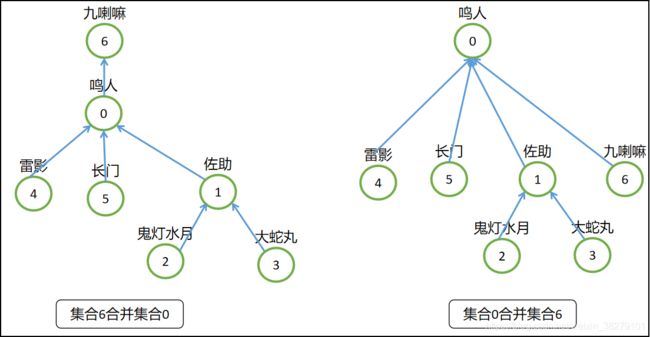
• 所以这启发我们：应该把简单的树往复杂的树上合并，即把树的深度小的树合并到树的深度大的树中，这样合并之后，每个元素到根结点的距离变成的元素个数最少。

(2)按秩合并的做法

       我们用rank[ ]数组来记录每个根结点对应的树的深度（如果不是根结点，则rank中的元素大小表示的是以当前结点作为根结点的子树的深度）；一开始，把所有元素的rank设为1，即自己就为一颗树，且深度为1；合并的时候，比较两个根结点，把rank较小者合并到较大者中去。

(2.1)按秩合并的初始化：

void init(int n){
    for(int i=0;i<n;i++){
        Parent[i]=i;
        Rank[i]=1;
    }
}

(2.2)按秩合并的合并代码：

//合并
void merge(int i,int j){
    int x = find(i),y = find(j); //分别找到结点i和结点j的根节点
    if(Rank[x] < Rank[y]){       //如果以x作为根结点的子树深度小于以y作为根结点的子树的深度，则把x合并到y中
        Parent[x]=y;
    }
    else{
        Parent[y]=x;
    }
    if(Rank[x] == Rank[y] && x != y){  //如果深度相同且根结点不同，以x为根结点的子树深度+1
        Rank[x]++;
    }
}

为什么深度相同，以x为根结点的子树深度要+1呢？

六、并查集类通用模板

//并查集类
class DisJointSetUnion
{
private:
    // 所有根结点相同的结点位于同一个集合中
    vector<int> parent;    // 双亲结点数组，记录该结点的双亲结点，用于查找该结点的根结点
    vector<int> rank;      // 秩数组，记录以该结点为根结点的树的深度，主要用于优化，在合并两个集合的时候，rank大的集合合并rank小的集合

public:
    DisJointSetUnion(int n)          //构造函数
    {
        for (int i = 0; i < n; i++)
        {
            parent.push_back(i);      //此时各自为王，自己就是一个集合
            rank.push_back(1);        //rank=1，此时每个结点自己就是一颗深度为1的树
        }
    }

    //查找根结点
    int find(int x)
    {
        if(x==parent[x])
            return x;
        else
        {
            parent[x] = find(parent[x]);   // 路径压缩， 遍历过程中的所有双亲结点直接指向根结点，减少后续查找次数
            return parent[x];
        }
    }

    void merge(int x,int y)
    {
        int rx = find(x);                    //查找x的根结点，即x所在集合的代表元素
        int ry = find(y);

        if (rx != ry)                           //如果不是同一个集合
        {
            if (rank[rx] < rank[ry])     //rank大的集合合并rank小的集合
            {
                swap(rx, ry);               //这里进行交换是为了保证rx的rank大于ry的rank，方便下面合并
            }

             parent[ry] = rx;              //rx 合并 ry

            if (rank[rx] == rank[ry])
                rank[rx] += 1;
        }
    }
};