【C语言刷题】猜名次、猜凶手、杨辉三角、杨氏矩阵、字符串左旋、判断是否为左旋子串
目录
一、猜名次
二、猜凶手
三、杨辉三角
解法一:
解法二
四、杨氏矩阵
解法一
解法二
五、字符串左旋
解法一
解法二
六、判断是否为字符串左旋字串
解法一
解法二
总结
一、猜名次
5位运动员参加了10米台跳水比赛,有人让他们预测比赛结果:
A选手说:B第二,我第三;
B选手说:我第二,E第四;
C选手说:我第一,D第二;
D选手说:C最后,我第三;
E选手说:我第四,A第一;
比赛结束后,每位选手都说对了一半,请编程确定比赛的名次。
对于这道题我们是这样思考的,五次循环遍历,穷举所有可能性,然后由于题目描述说每人说对了一半,而他们正好每人说了两句话,那么也就是我们让两句话都与真进行比较,如果为真则为1,如果为假则为0,加起来就是1即可。具体代码如下
#include
int main()
{
int a = 0;
int b = 0;
int c = 0;
int d = 0;
int e = 0;
for (a = 1; a <= 5; a++)
{
for (b = 1; b <= 5; b++)
{
for (c = 1; c <= 5; c++)
{
for (d = 1; d <= 5; d++)
{
for (e = 1; e <= 5; e++)
{
if ( (b == 2) + (a == 3) == 1
&& (b == 2) + (e == 4) == 1
&& (c == 1) + (d == 2) == 1
&& (c == 5) + (d == 3) == 1
&& (e == 4) + (a == 1) == 1
&& a*b*c*d*e==120)
{
printf("A:%d B:%d C:%d D:%d E:%d\n", a, b, c, d, e);
}
}
}
}
}
}
return 0;
} 要注意的是,为了保证不会出现重复,我们使用一个相乘来缩小结果
运行结果如下
二、猜凶手
日本某地发生了一件谋杀案,警察通过排查确定杀人凶手必为4个嫌疑犯的一个。
以下为4个嫌疑犯的供词:
A说:不是我。
B说:是C。
C说:是D。
D说:C在胡说
已知3个人说了真话,1个人说的是假话。
现在请根据这些信息,写一个程序来确定到底谁是凶手。
对于这道题,我们的思路和上一题基本一致,我们穷举每一个人都可能使凶手,然后判断每个人的话是否为真,最终相加结果为3即可
#include
int main()
{
char killer;
for (killer = 'A'; killer <= 'D'; killer++)
{
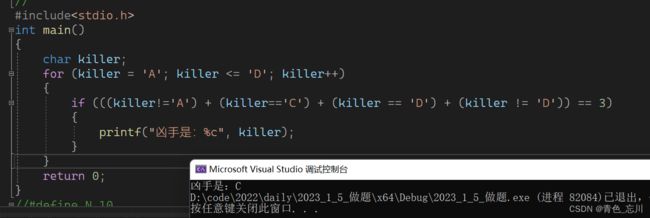
if (((killer!='A') + (killer=='C') + (killer == 'D') + (killer != 'D')) == 3)
{
printf("凶手是:%c", killer);
}
}
return 0;
} 三、杨辉三角
在屏幕上打印杨辉三角。
1
1 1
1 2 1
1 3 3 1
……
解法一:
对于这道题,我们最简单最暴力的思路就是直接创建一个二维数组,然后将杨辉三角的数据都存储到这个数组中去,我们这个打印的杨辉三角其实它是把前面的空格都给删除了,就一边倒的样子,导致有点跟数学中的杨辉三角长得有点不太一样。但是没关系它也是有规律的
它的规律是这样的:第一列和主对角线都是1,然后其他位置的元素都是由于这个位置的上方的元素加上左上角的元素的。所以我们可以写出如下代码
#define N 10
#include
int main()
{
int arr[N][N] = { 0 };
int i = 0;
int j = 0;
for (i = 0; i < N; i++)
{
for (j = 0; j < N; j++)
{
if (j == 0 || i == j)
{
arr[i][j] = 1;
}
if (i > 0 && j > 0)
{
arr[i][j] = arr[i - 1][j] + arr[i - 1][j - 1];
}
}
}
for (i = 0; i < N; i++)
{
for (j = 0; j < N; j++)
{
if (i >= j)
{
printf("%d ", arr[i][j]);
}
}
printf("\n");
}
return 0;
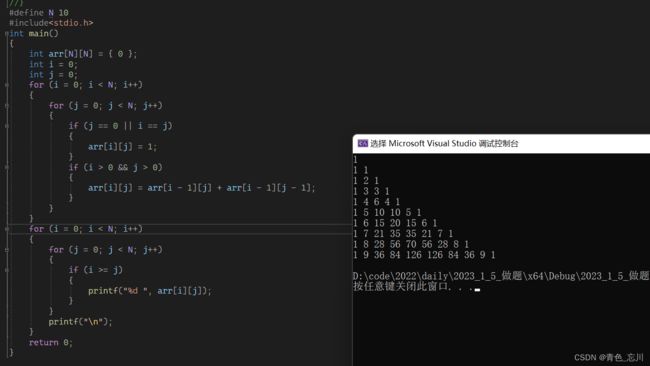
} 也就是,一开始让整个数组都置为0,然后我们让对角线的第一列的元素都置为1。除此以外的,其他元素也就是i>0并且j>0的时候,都是由上方元素和左上方元素相加得到的。这个思路很简单
运行结果如下
解法二
其实我们也能发现,第一种解法的空间复杂度太大了,始O(N^2),那么我们可不可以使用一个一维数组来解决呢?答案当然是可以的。
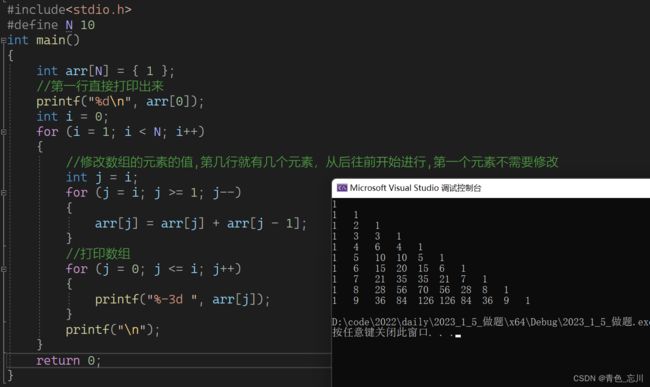
我们的思路是这样的,先创建一个一维数组,然后这个数组每次存储一行的数据。根据我们的规律,第一个元素必须得是1才可以。这个是不可以修改的。然后其他位置的元素就简单了,我们从后往前赋值,就是它原来这个位置的元素加上前一个元素的值。所以我们得到代码如下
#include
#define N 10
int main()
{
int arr[N] = { 1 };
//第一行直接打印出来
printf("%d\n", arr[0]);
int i = 0;
for (i = 1; i < N; i++)
{
//修改数组的元素的值,第几行就有几个元素,从后往前开始进行,第一个元素不需要修改
int j = i;
for (j = i; j >= 1; j--)
{
arr[j] = arr[j] + arr[j - 1];
}
//打印数组
for (j = 0; j <= i; j++)
{
printf("%-3d ", arr[j]);
}
printf("\n");
}
return 0;
} 四、杨氏矩阵
有一个数字矩阵,矩阵的每行从左到右是递增的,矩阵从上到下是递增的,请编写程序在这样的矩阵中查找某个数字是否存在。
要求:时间复杂度不超过O(N);
解法一
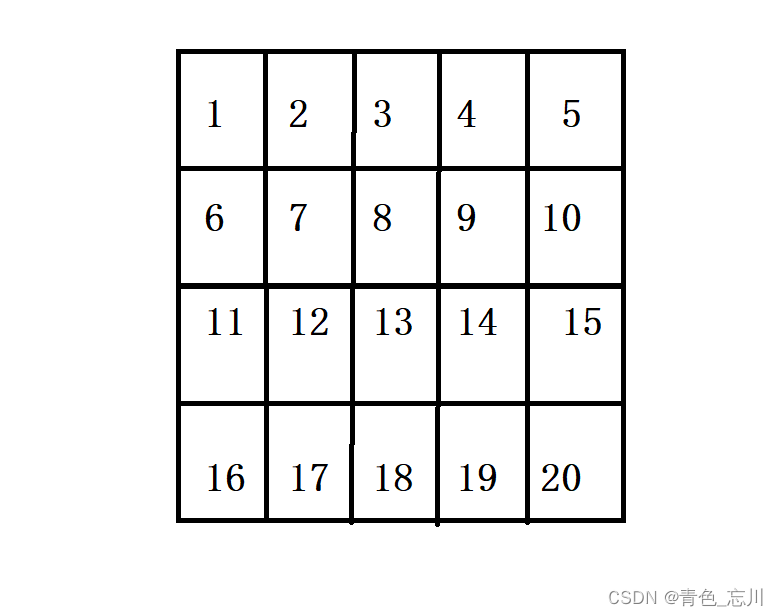
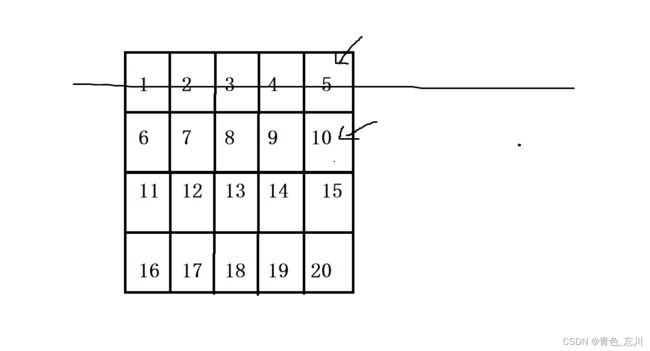
假如说我们有这样一个矩阵
我们可以从右上角开始找起来,如果比这个数大,则砍掉一行,如果比这个数字小,则砍掉一列,假如说我们要找13,那么一开始13比5大。砍掉一行
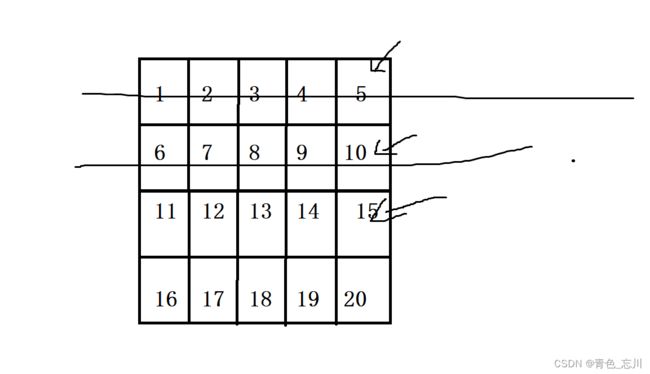
13还是比10大,继续砍掉一行
13比15小,砍掉一列
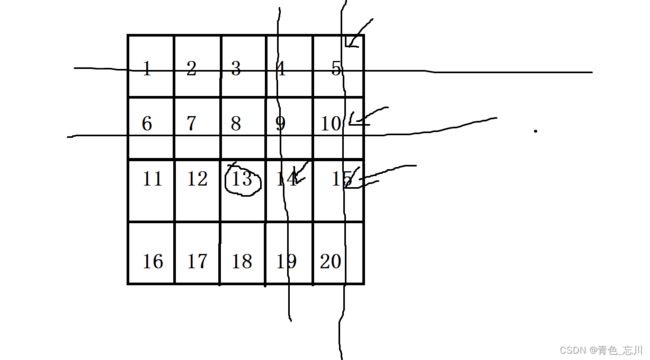
继续砍掉一列
最终我们就找到了这个数了。而且这种算法的最坏情况就是左下角是2N,最好情况是右上角是1,所以平均时间复杂度为O(N)
代码如下
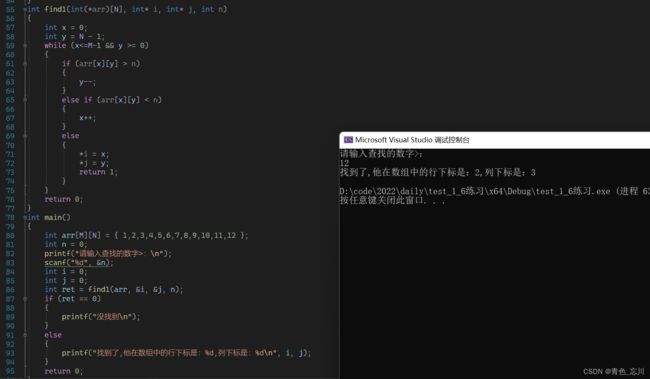
#define M 3
#define N 4
int find1(int(*arr)[N], int* i, int* j, int n)
{
int x = 0;
int y = N - 1;
while (x<=M-1 && y >= 0)
{
if (arr[x][y] > n)
{
y--;
}
else if (arr[x][y] < n)
{
x++;
}
else
{
*i = x;
*j = y;
return 1;
}
}
return 0;
}
int main()
{
int arr[M][N] = { 1,2,3,4,5,6,7,8,9,10,11,12 };
int n = 0;
printf("请输入查找的数字>:\n");
scanf("%d", &n);
int i = 0;
int j = 0;
int ret = find1(arr, &i, &j, n);
if (ret == 0)
{
printf("没找到\n");
}
else
{
printf("找到了,他在数组中的行下标是:%d,列下标是:%d\n", i, j);
}
return 0;
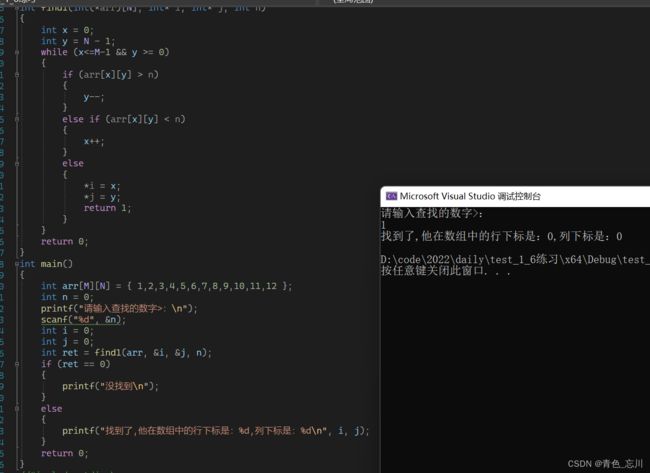
}当然对于这种方法而言,也可以从左下角进行入手。但是绝对不可以从左上角和右下角入手
解法二
其实对于上面的方法还不是最优的解法,我们之前说过二分查找算法,我们这道题也可以使用二分法,我们只需要先对第一列进行二分查找,然后找到行下标,然后在对行二分查找,就找到了行下标了
#define _CRT_SECURE_NO_WARNINGS 1
#define M 3
#define N 4
#include
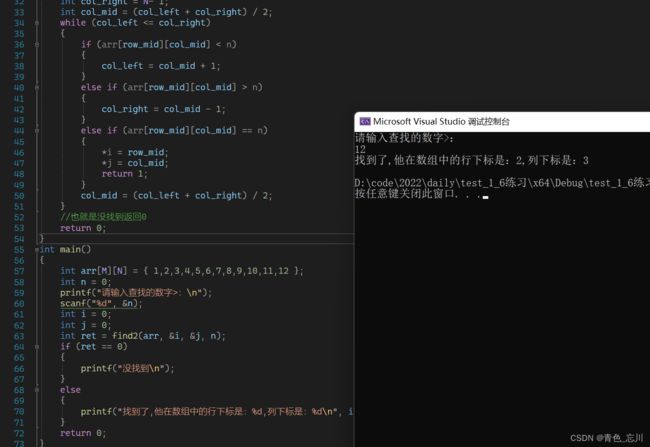
int find2(int arr[M][N], int* i, int* j, int n)
{
//先在第一列中找到行下标的范围,也就是纵向寻找
int row_left = 0;
int row_right = M - 1;
int row_mid = (row_left + row_right) / 2;
while (row_left <= row_right)
{
if (arr[row_mid][0] < n)
{
row_left = row_mid + 1;
}
else if (arr[row_mid][0] > n)
{
row_right = row_mid - 1;
}
else if (arr[row_mid][0] == n)
{
*i = row_mid;
*j = 0;
//返回1代表找到了,返回0代表没找到
return 1;
}
row_mid = (row_left + row_right) / 2;
}
//第一列中已经找出来列下标了,现在该让行下标不动、列下标开始变化了,也就是横向寻找
int col_left = 0;
int col_right = N- 1;
int col_mid = (col_left + col_right) / 2;
while (col_left <= col_right)
{
if (arr[row_mid][col_mid] < n)
{
col_left = col_mid + 1;
}
else if (arr[row_mid][col_mid] > n)
{
col_right = col_mid - 1;
}
else if (arr[row_mid][col_mid] == n)
{
*i = row_mid;
*j = col_mid;
return 1;
}
col_mid = (col_left + col_right) / 2;
}
//也就是没找到返回0
return 0;
}
int main()
{
int arr[M][N] = { 1,2,3,4,5,6,7,8,9,10,11,12 };
int n = 0;
printf("请输入查找的数字>:\n");
scanf("%d", &n);
int i = 0;
int j = 0;
int ret = find2(arr, &i, &j, n);
if (ret == 0)
{
printf("没找到\n");
}
else
{
printf("找到了,他在数组中的行下标是:%d,列下标是:%d\n", i, j);
}
return 0;
} 运行结果为
五、字符串左旋
实现一个函数,可以左旋字符串中的k个字符。
例如:
ABCD左旋一个字符得到BCDA
ABCD左旋两个字符得到CDAB
解法一
对于这道题我们最最最简单的思路就是,先想办法左旋一个字符,然后重复k次,而要左旋一个字符的话,我们可以将第一个字符放到一个临时变量里面,然后我们将后面的元素都覆盖到前面来,最后将这个临时变量的放到最后一个即可。代码如下
#include
#include
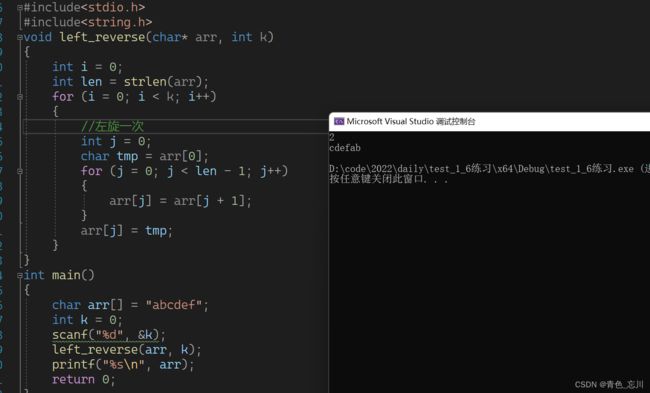
void left_reverse(char* arr, int k)
{
int i = 0;
int len = strlen(arr);
for (i = 0; i < k; i++)
{
//左旋一次
int j = 0;
char tmp = arr[0];
for (j = 0; j < len - 1; j++)
{
arr[j] = arr[j + 1];
}
arr[j] = tmp;
}
}
int main()
{
char arr[] = "abcdef";
int k = 0;
scanf("%d", &k);
left_reverse(arr, k);
printf("%s\n", arr);
return 0;
} 解法二
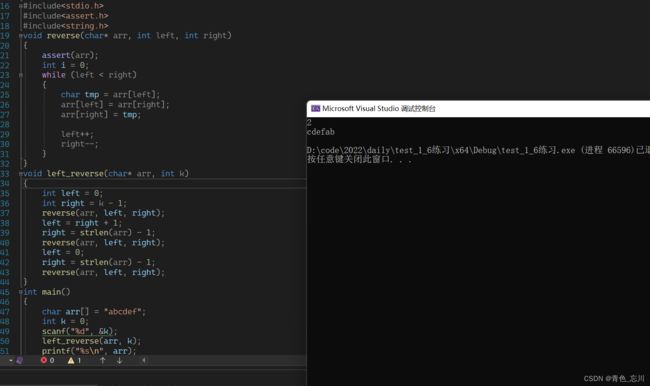
解法二比较神奇,我们先前前k个元素给逆序,然后将其余的元素给逆序,最后整体逆序,经历三次逆序后,也能解决问题
#include
#include
#include
void reverse(char* arr, int left, int right)
{
assert(arr);
int i = 0;
while (left < right)
{
char tmp = arr[left];
arr[left] = arr[right];
arr[right] = tmp;
left++;
right--;
}
}
void left_reverse(char* arr, int k)
{
int left = 0;
int right = k - 1;
reverse(arr, left, right);
left = right + 1;
right = strlen(arr) - 1;
reverse(arr, left, right);
left = 0;
right = strlen(arr) - 1;
reverse(arr, left, right);
}
int main()
{
char arr[] = "abcdef";
int k = 0;
scanf("%d", &k);
left_reverse(arr, k);
printf("%s\n", arr);
return 0;
} 六、判断是否为字符串左旋字串
写一个函数,判断一个字符串是否为另外一个字符串旋转之后的字符串。
例如:给定s1 =AABCD和s2 = BCDAA,返回1
给定s1=abcd和s2=ACBD,返回0.
AABCD左旋一个字符得到ABCDA
AABCD左旋两个字符得到BCDAA
AABCD右旋一个字符得到DAABC
解法一
对于这道题,我们最简单的思路就是利用第五题函数,穷举所有旋转可能性判断是否相等
代码如下
#include
#include
#include
void reverse(char* arr, int left, int right)
{
assert(arr);
int i = 0;
while (left < right)
{
char tmp = arr[left];
arr[left] = arr[right];
arr[right] = tmp;
left++;
right--;
}
}
void left_reverse(char* arr, int k)
{
int left = 0;
int right = k - 1;
reverse(arr, left, right);
left = right + 1;
right = strlen(arr) - 1;
reverse(arr, left, right);
left = 0;
right = strlen(arr) - 1;
reverse(arr, left, right);
}
int is_reverse(char* arr1,char* arr2)
{
int i = 0;
int len = strlen(arr1);
for (i = 0; i < len; i++)
{
if (strcmp(arr1, arr2) == 0)
{
return 1;
}
left_reverse(arr1, 1);
}
return 0;
}
int main()
{
char arr1[100] = { 0 };
char arr2[100] = { 0 };
gets(arr1);
gets(arr2);
int ret = is_reverse(arr1, arr2);
if (ret == 1)
{
printf("是左旋得到的\n");
}
else
{
printf("不是左旋得到的\n");
}
return 0;
}
解法二
我们还有一种思路就是利用库函数,使用strncat这个函数对arr1追加一个arr1,这样arr1中肯定包含所有的左旋情况,这样我们只需要在arr1中找出子串即可,而找出子串也有自己的库函数,strstr
由此我们便可以很简洁的完成我们的代码了
#include
#include
int is_reverse(char* arr1, char* arr2)
{
int len1 = strlen(arr1);
int len2 = strlen(arr2);
if (len1 != len2)
{
return 0;
}
strncat(arr1, arr1, len1);
if (strstr(arr1, arr2) != NULL)
{
return 1;
}
return 0;
}
int main()
{
char arr1[100] = { 0 };
char arr2[100] = { 0 };
gets(arr1);
gets(arr2);
int ret = is_reverse(arr1, arr2);
if (ret == 1)
{
printf("是左旋得到的\n");
}
else
{
printf("不是左旋得到的\n");
}
return 0;
}
总结
本小节讲解了猜名次、猜凶手、杨辉三角、杨氏矩阵、字符串左旋、判断是否为左旋子串这几个经典的题目
如果对你有帮助的话,不要忘记点赞加收藏哦!!!
想获得更多优质内容,一定要关注我哦!!!