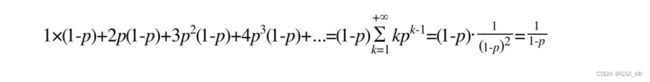高阶数据结构 -------- 跳表
目录
1.什么是跳表 - Skiplist
2.skiplist的效率如何保证？
3.Skiplist实现
(1)整体代码
(2)节点设计
(3) Skiplist成员变量 和 构造函数
(4)search函数，查找数据
(5)FindPrevNode函数
(6)add函数
(7)erase函数
(8)获取随机数函数
4.skiplist跟平衡搜索树和哈希表的对比
1.什么是跳表 - Skiplist
- skiplist本质上也是一种查找结构，用于解决算法中的查找问题，跟平衡搜索树和哈希表的价值是一样的，可以作为key或者key/value的查找模型。
- skiplist是由William Pugh发明的，最早出现于他在1990年发表的论文《Skip Lists: AProbabilistic Alternative to Balanced Trees》。skiplist，顾名思义，首先它是一个list。实际上，它是在有序链表的基础上发展起来的。如果是一个有序的链表在查找数据的时间复杂度是O(N)。
William Pugh开始的优化思路：
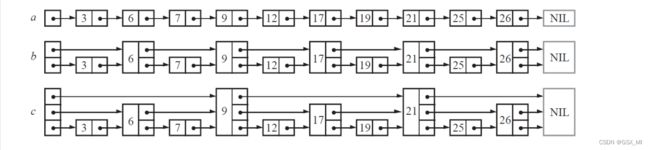
- ①假如我们每相邻两个节点升高一层，增加一个指针，让指针指向下下个节点，如下图b所示。这样所有新增加的指针连成了一个新的链表，但它包含的节点个数只有原来的一半。由于新增加的指针，我们不再需要与链表中每个节点逐个进行比较了，需要比较的节点数大概只有原来的一半。
- ②以此类推，我们可以在第二层新产生的链表上，继续为每相邻的两个节点升高一层，增加一个指针，从而产生第三层链表。如下图c，这样搜索效率就进一步提高了。
- ③skiplist正是受这种多层链表的想法的启发而设计出来的。实际上，按照上面生成链表的方式，上面每一层链表的节点个数，是下面一层的节点个数的一半，这样查找过程就非常类似二分查找，使得查找的时间复杂度可以降低到O(log n)。但是这个结构在插入删除数据的时候有很大的问题，插入或者删除一个节点之后，就会打乱上下相邻两层链表上节点个数严格的2:1的对应关系。如果要维持这种对应关系，就必须把新插入的节点后面的所有节点（也包括新插入的节点）重新进行调整，这会让时间复杂度重新蜕化成O(n)。
- ④skiplist的设计为了避免这种问题，做了一个大胆的处理，不再严格要求对应比例关系，而是插入一个节点的时候随机出一个层数。这样每次插入和删除都不需要考虑其他节点的层数，这样就好处理多了。细节过程入下图：
2.skiplist的效率如何保证？
①上面说到，skiplist插入一个节点时随机出一个层数，听起来怎么这么随意，如何保证搜索时的效率呢？
②这里首先要细节分析的是这个随机层数是怎么来的。一般跳表会设计一个最大层数maxLevel的限制，其次会设置一个多增加一层的概率p。那么计算这个随机层数的伪代码如下图：
③在Redis的skiplist实现中，这两个参数的取值为：
p = 1/4
maxLevel = 32④根据前面randomLevel()的伪码，我们很容易看出，产生越高的节点层数，概率越低。定量的分析如下：
- 节点层数至少为1。而大于1的节点层数，满足一个概率分布。
- 节点层数恰好等于1的概率为1-p。
- 节点层数大于等于2的概率为p，而节点层数恰好等于2的概率为p(1-p)。
- 节点层数大于等于3的概率为p^2，而节点层数恰好等于3的概率为p^2*(1-p)。
- 节点层数大于等于4的概率为p^3，而节点层数恰好等于4的概率为p^3*(1-p)。
- …
⑤因此，一个节点的平均层数（也即包含的平均指针数目），计算如下：
现在很容易计算出：
- 当p=1/2时，每个节点所包含的平均指针数目为2；
- 当p=1/4时，每个节点所包含的平均指针数目为1.33。
补充文章，帮助理解
http://zhangtielei.com/posts/blog-redis-skiplist.html
3.Skiplist实现
(1)整体代码
#include
#include
#include
#include
#include
using namespace std;
namespace XM
{
struct SkiplistNode
{
int _val;
vector _nextV;
SkiplistNode(int val, int level)
:_val(val)
, _nextV(level, nullptr)
{}
};
class Skiplist
{
typedef SkiplistNode Node;
public:
Skiplist()
{
srand(time(0)); //C语言获取随机值
//头结点，刚开始给1层 ; 后序有效的最高层变了，层数会提高
_head = new Node(-1, 1);
}
bool search(int target)
{
Node* cur = _head;
int level = _head->_nextV.size() - 1; //这里表示最上层下标
//结束条件 - 画图
while (level >= 0)
{
// 目标值比下一个节点值要大，向右走
// 下一个节点是空(尾) / 目标值比下一个节点值要小，向下走
if (cur->_nextV[level] && cur->_nextV[level]->_val < target)
{
//向右走
cur = cur->_nextV[level];
}
else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val > target)
{
//向下走
level--;
}
else
{
return true;
}
}
return false;
}
//添加新的Node 要找到每一层前面的Node
vector FindPrevNode(int num)
{
Node* cur = _head;
int level = _head->_nextV.size() - 1; //最高层的下标
// 初始化，前一个节点指针都为_head
vector prevV(level + 1, _head);
//和search有点像
while (level >= 0)
{
// 目标值比下一个节点值要大，向右走
// 下一个节点是空(尾) / 目标值比下一个节点值要小，向下走
if (cur->_nextV[level] && cur->_nextV[level]->_val < num)
{
//向右走,层没有变
cur = cur->_nextV[level];
}
else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val >= num)
{
//向下走之前记录当前层Node
prevV[level] = cur;
//向下走
level--;
}
}
return prevV;
}
void add(int num)
{
//获取前一个Node的集合
vector prevV = FindPrevNode(num);
//构造新节点并初始化，随机获取层数
int n = RandomLevel();
Node* newNode = new Node(num, n);
// 如果n超过当前最大的层数，那就升高一下_head的层数
//为什么不一开始就把head升到最高？
//一开始升到最高，后序的查找有很多是无用的，如果要提高效率还需要一个变量记录当前最高层是什么
//所以我们不直接把head升到最高,且利用一个变量记录最高层，当新插入数据的层数 > 最高层时我们只需要增加层数即可
if (n > _head->_nextV.size())
{
_head->_nextV.resize(n, nullptr); //后面多开的空间填充nullptr,之前的空间值不变
prevV.resize(n, _head);
}
for (int i = 0; i < n; ++i)
{
newNode->_nextV[i] = prevV[i]->_nextV[i];
prevV[i]->_nextV[i] = newNode;
}
}
bool erase(int num)
{
vector prevV = FindPrevNode(num);
//val不在表中 或者 第一层的下一个不是val这两种情况
if (prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val != num)
{
return false;
}
else
{
Node* del = prevV[0]->_nextV[0];
//将del前后的每一层指针连接起来
for (size_t i = 0; i < del->_nextV.size(); ++i)
{
prevV[i]->_nextV[i] = del->_nextV[i];
}
delete del;
//如果删除的有最高层节点，把头结点层数降一下
int i = _head->_nextV.size() - 1;
while (i >= 0)
{
if (_head->_nextV[i] == nullptr)
{
--i;
}
else
{
break;
}
}
//重新调整_nextV的大小
_head->_nextV.resize(i + 1);
return true;
}
}
int RandomLevel_C() //C语言随机产生数字
{
size_t level = 1;
// rand() ->[0, RAND_MAX]之间
while (rand() <= RAND_MAX * _p && level < _maxLevel)
{
++level;
}
return level;
}
int RandomLevel() //C++11随机产生数字，是均匀分布的
{
//定义成静态的只会在第一次调用时跑一次，后面再次调用就不会跑了
static std::default_random_engine generator(std::chrono::system_clock::now().time_since_epoch().count());
static std::uniform_real_distribution distribution(0.0, 1.0);
size_t level = 1;
while (distribution(generator) <= _p && level < _maxLevel)
{
++level;
}
return level;
}
//打印出来那个结构
void Print()
{
Node* cur = _head;
while (cur)
{
printf("%-2d\n", cur->_val);
// 打印每个每个cur节点
for (auto e : cur->_nextV)
{
printf("%2s", "↓");
}
printf("\n");
cur = cur->_nextV[0];
}
}
private:
Node* _head;
size_t _maxLevel = 32;
double _p = 0.25;
};
//验证随机数是均匀分布的
void RandomTest()
{
//定义成静态的只会在第一次调用时跑一次，后面再次调用就不会跑了
static std::default_random_engine generator(std::chrono::system_clock::now().time_since_epoch().count());
static std::uniform_real_distribution distribution(0.0, 1.0);
size_t count = 0;
for (int i = 0; i < 1000; ++i)
{
if (distribution(generator) <= 0.25)
{
++count;
}
}
cout << count << endl;
}
}
(2)节点设计
- 存储节点值 int _val
- 存储下一个节点指针数组 _nextV , 通过传入的level控制指针数组大小
struct SkiplistNode
{
int _val;
vector _nextV;
SkiplistNode(int val, int level)
:_val(val)
, _nextV(level, nullptr)
{}
};
(3) Skiplist成员变量 和 构造函数
- 构造函数中srand(time(0)) ,先设置种子 后序 rand()函数产生随机数需要
- 构造函数中初始化_head, 值设置为 -1 ，先设置一层 ；后序有需要再调整
public:
Skiplist()
{
srand(time(0)); //C语言获取随机值
//头结点，刚开始给1层 ; 后序有效的最高层变了，层数会提高
_head = new Node(-1, 1);
}
private:
Node* _head; //头结点
size_t _maxLevel = 32; //设置节点最高层
double _p = 0.25; //设置多增加一层的概率p
(4)search函数，查找数据
①查找数据示意图
②代码思路
- 记录头结点和头结点最高层下标
- 只有level >=0 时查找才有效，否则返回false
- 如果当前节点的值 > 目标值则向右走
- 如果当前节点的值 < 目标值 或者 同一层下一个节点为空(下标--) 则向下走
③模拟实现
bool search(int target)
{
Node* cur = _head;
int level = _head->_nextV.size() - 1; //这里表示最上层下标
//结束条件 - 画图
while (level >= 0)
{
// 目标值比下一个节点值要大，向右走
// 下一个节点是空(尾) / 目标值比下一个节点值要小，向下走
if (cur->_nextV[level] && cur->_nextV[level]->_val < target)
{
//向右走
cur = cur->_nextV[level];
}
else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val > target)
{
//向下走
level--;
}
else
{
return true;
}
}
return false;
}
(5)FindPrevNode函数
①设计该函数的目的
- add函数添加新节点要找到新节点位置之前的每一层前一个节点进行连接
- erase函数删除节点要找到该节点每一层前一个节点 与 该节点每一层的后一个节点进行连接
- 使代码简洁，设计了FindPrevNode函数，实现代码的复用
②函数设计思路
- 记录头结点和头结点最高层下标 ，创建vector对象存储目标值的前一个节点并初始化
- 只有level >=0 时查找才有效
- 如果当前节点的值 > 目标值则向右走 ，当前层没有变化
- 如果当前节点的值 < 目标值 或者 同一层下一个节点为空(下标--) 则向下走 ，向下走之前记录当前层Node
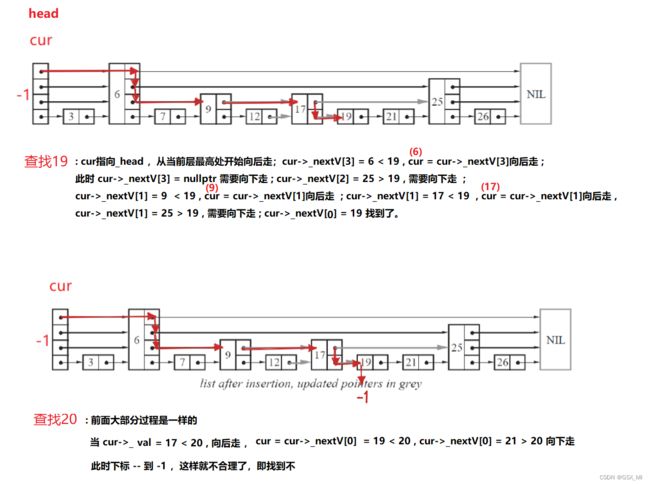
③假设找 num = 19 ，过程如图示
④代码实现
//添加新的Node 要找到每一层前面的Node
vector FindPrevNode(int num)
{
Node* cur = _head;
int level = _head->_nextV.size() - 1; //最高层的下标
// 初始化，前一个节点指针都为_head
vector prevV(level + 1, _head);
//和search有点像
while (level >= 0)
{
// 目标值比下一个节点值要大，向右走
// 下一个节点是空(尾) / 目标值比下一个节点值要小，向下走
if (cur->_nextV[level] && cur->_nextV[level]->_val < num)
{
//向右走,层没有变
cur = cur->_nextV[level];
}
else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val >= num)
{
//向下走之前记录当前层Node
prevV[level] = cur;
//向下走
level--;
}
}
return prevV;
}
(6)add函数
①函数设计思路
- 获取要添加数据的前一个Node的集合
- 构建新节点并初始化，随机获取层数
- 如果随机获取的层数n超过当前最大的层数，那就升高一下_head的层数
- 利用前一个Node集合 prevV 和 当前节点的每一层建立连接关系
②为什么不一开始就把_head层数升到最高？
- 一开始升到最高，后序的查找有很多是无用的，如果要提高效率还需要一个变量记录当前最高层是什么
- 所以我们不直接把head升到最高,且利用一个变量记录最高层，当新插入数据的层数 > 最高层时我们只需要增加层数即可
③代码实现
void add(int num)
{
//获取前一个Node的集合
vector prevV = FindPrevNode(num);
//构造新节点并初始化，随机获取层数
int n = RandomLevel();
Node* newNode = new Node(num, n);
// 如果n超过当前最大的层数，那就升高一下_head的层数
//为什么不一开始就把head升到最高？
//一开始升到最高，后序的查找有很多是无用的，如果要提高效率还需要一个变量记录当前最高层是什么
//所以我们不直接把head升到最高,且利用一个变量记录最高层，当新插入数据的层数 > 最高层时我们只需要增加层数即可
if (n > _head->_nextV.size())
{
_head->_nextV.resize(n, nullptr); //后面多开的空间填充nullptr,之前的空间值不变
prevV.resize(n, _head);
}
for (int i = 0; i < n; ++i)
{
newNode->_nextV[i] = prevV[i]->_nextV[i];
prevV[i]->_nextV[i] = newNode;
}
}
(7)erase函数
①函数设计思路
- 获取要删除数据的前一个Node的集合 prevV
- 如果 prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val != num 即未找到该数据,返回false
- 否则记录要删除的Node ，去除前后连接关系，然后delete 释放资源
- 如果删除的有最高层节点，把头结点层数降一下，重新调整头结点层数，这样下次查找时就不会从无用的最高层开始查找 (这个过程做不做都行，提升不太大)
②代码实现
bool erase(int num)
{
vector prevV = FindPrevNode(num);
//val不在表中 或者 第一层的下一个不是val这两种情况
if (prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val != num)
{
return false;
}
else
{
Node* del = prevV[0]->_nextV[0];
//将del前后的每一层指针连接起来
for (size_t i = 0; i < del->_nextV.size(); ++i)
{
prevV[i]->_nextV[i] = del->_nextV[i];
}
delete del;
//如果删除的有最高层节点，把头结点层数降一下
int i = _head->_nextV.size() - 1;
while (i >= 0)
{
if (_head->_nextV[i] == nullptr)
{
--i;
}
else
{
break;
}
}
//重新调整_nextV的大小
_head->_nextV.resize(i + 1);
return true;
}
}
(8)获取随机数函数
①利用C语言提供的函数获取
- 初始化时间种子，调用rand()函数获取随机值
- rand() 获取的值范围在 [0 , RAND_MAX]之间 ； 当 rand() <= RAND_MAX * _p && level < _maxLevel 时++level
- 这样获取level的做法很巧妙，但是C语言提供rand()函数值是随机的没有规律
②利用C++11 提供的函数
- std::uniform_real_distribution
distribution(0.0, 1.0) ；随机生成0.0 - 1.0的数，但是生成的数是均匀分布的 - 进行代码测试验证随机数是均匀分布的，平均来说随机生成数字 < 0.25 概率是均匀的
③代码实现
int RandomLevel_C() //C语言随机产生数字
{
size_t level = 1;
// rand() ->[0, RAND_MAX]之间
while (rand() <= RAND_MAX * _p && level < _maxLevel)
{
++level;
}
return level;
}
int RandomLevel() //C++11随机产生数字，是均匀分布的
{
//定义成静态的只会在第一次调用时跑一次，后面再次调用就不会跑了
static std::default_random_engine generator(std::chrono::system_clock::now().time_since_epoch().count());
static std::uniform_real_distribution distribution(0.0, 1.0);
size_t level = 1;
while (distribution(generator) <= _p && level < _maxLevel)
{
++level;
}
return level;
}
4.skiplist跟平衡搜索树和哈希表的对比
(1)skiplist相比平衡搜索树(AVL树和红黑树)对比，都可以做到遍历数据有序，时间复杂度也差不多。skiplist的优势是：
- a、skiplist实现简单，容易控制。平衡树增删查改遍历都更复杂.
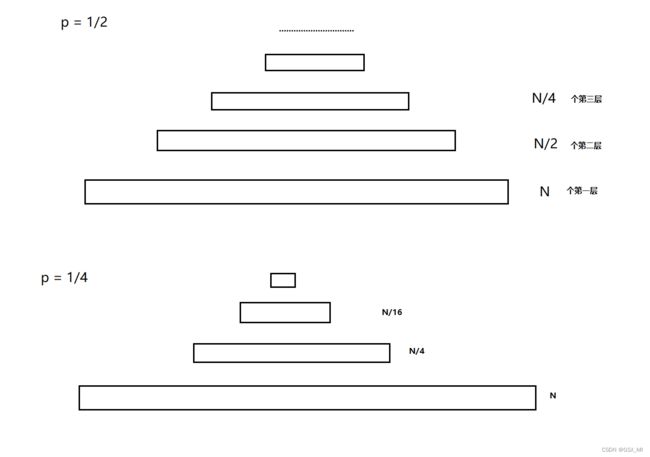
- b、skiplist的额外空间消耗更低。平衡树节点存储每个值有三叉链，平衡因子/颜色等消耗。skiplist中p=1/2时，每个节点所包含的平均指针数目为2；skiplist中p=1/4时，每个节点所包含的平均指针数目为1.33；
(2) skiplist相比哈希表而言，就没有那么大的优势了。相比而言
- a、哈希表平均时间复杂度是O(1)，比skiplist快。
- b、但是哈希表空间消耗略多一点。
(3)skiplist优势如下：
- a、遍历数据有序
- b、skiplist空间消耗略小一点，哈希表存在链接指针和表空间消耗。
- c、哈希表扩容有性能损耗。
- d、哈希表再极端场景下哈希冲突高，效率下降厉害，需要红黑树补足接力。
(4)小结
- 跳表的最大优势还是简单,有一些不足就是当数据量小的时候数据密, 数据量大的时候还好；假设1000个数据可能前半段30%的数据是一层, 后面有2层，3层的节点 ;但是这种概率非常的低。
- 跳表的结果看起来复杂，但是实现比较简单