数据结构--B树
基本搜索结构
我们先来回顾一下我们的数据结构,数据结构管理数据
1.简单地将数据存起来
2.除了存储数据,还需要可以快速搜索数据
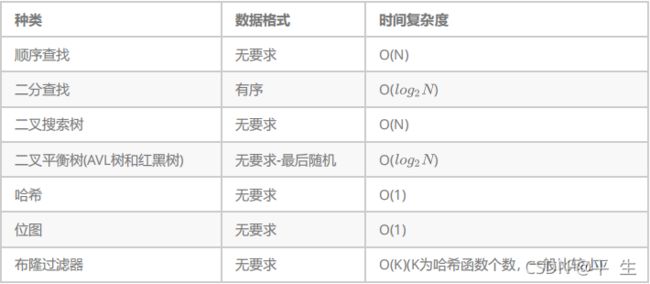
搜索
1.搜索二叉树,极端情况下退化,类似单支,效率就变成了O(N)
2.为了解决上面的问题,提出平衡树的概念,AVL树,红黑树。--O(logN) --map/set
3.有没有更好的数据结构,哈希/散列表--O(1) --unordered_map/unordered_set
4.未深入了解的数据结构--跳表,字典树
我们上面的结构都是为了完成内存中数据的搜索查找问题
但如果我们的数据量很多,在内存中存不下,我们的数据要存储在磁盘中,上面的数据结构效果就不好了,B树可以很好地解决这里的问题
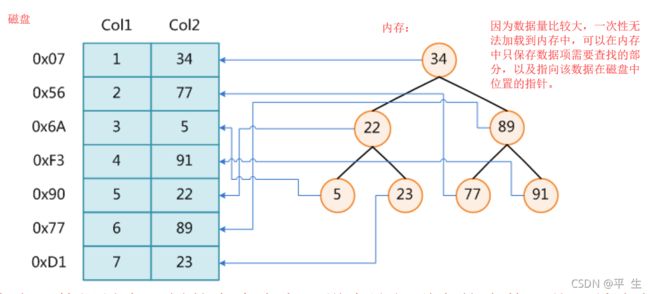
1.假设我们用的是红黑树或者AVL树,数据存在磁盘中,会有什么问题?
假设数据在磁盘中,树的节点中仅仅存的是在磁盘上的一个地址,我们的查找复杂度为O(logN),在我们的内存中,logN次内存访问是非常快的,但是在磁盘中,logN次IO访问,非常慢,还需要再快一点
这时我们想到了使用哈希表,查找次数变为了O(1),但其实也是不行的,O(!)并不是1次,而是常数次的意思,在极端情况下,哈希表冲突的很厉害,一个桶中的数据会很多,效果就下降的厉害
哈希表看起来快
问题1:可能并不那么稳定
问题2:哈希表存在很多附带数据,(表结构,节点中的指针等),数据量很大时,内存占用很多,其实我们的红黑树与AVL树也是有这样的问题的
B-树概念
因为上面的这个问题,我们引入了适合外查找的B树
1970 年, R.Bayer 和 E.mccreight 提出了一种适合外查找的树,它是一种平衡的多叉树,称为 B 树 。 一棵 M 阶 (M>2) 的 B 树,是一棵平衡的 M 路平衡搜索树,可以是空树 或者满足一下性质:1. 根节点至少有两个孩子2. 每个非根节点至少有 M/2( 上取整 ) 个孩子 , 至多有 M 个孩子3. 每个非根节点至少有 M/2-1( 上取整 ) 个关键字 , 至多有 M-1 个关键字,并且以升序排列4. key[i] 和 key[i+1] 之间的孩子节点的值介于 key[i] 、 key[i+1] 之间5. 所有的叶子节点都在同一层
总结:
根节点:关键字数量为[1,M-1],孩子数量未[2,M]
非根节点:关键字数量为[M/2-1,M-1],孩子数量[M/2,M]
每个节点中,孩子的数量比关键字的数量永远多一个
当我们了解了这个结构,我们可以初步的将B的结构搭建出来
template
struct BTreeNode//节点结构
{
//孩子的数量比关键字的数量多一个
pair _kv[M - 1];//关键字
BTreeNode* _subs[M];//孩子节点
BTreeNode* _parent;//父节点
size_t _kvSize;//关键字长度
};
template
class BTree
{
typedef BTreeNode Node;
private:
Node* _root;
}; B-树的插入分析
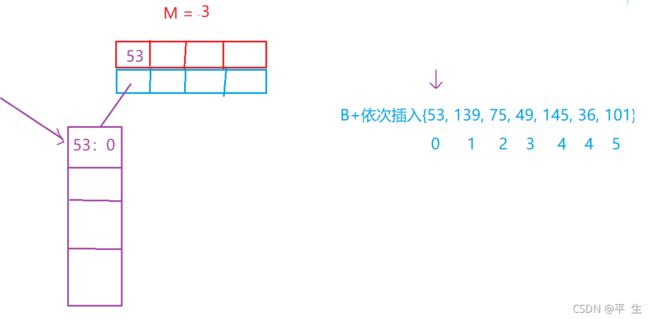
现在我们来模拟一下B树的构建过程
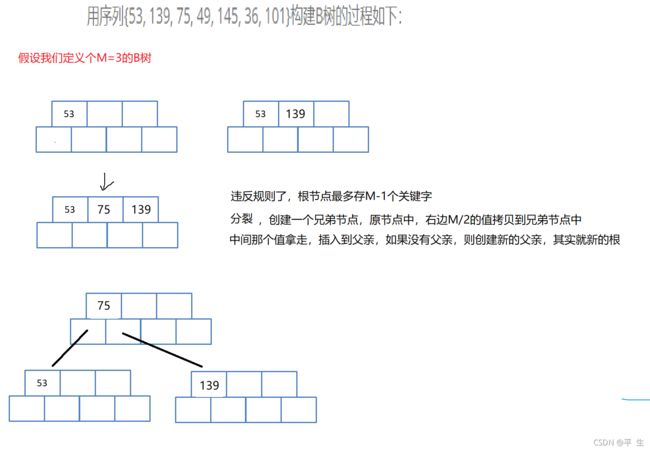
首先,我们插入53,正常插入,插入139,比53大,插到53右边,正常插入
当我们要插入75时,75比53大,139小,所以139后移,插在中间,但是此时就违反了B树根节点最多存M-1个关键字这个条件,所以我们这里的解决方法是分裂
创建出一个兄弟节点,将M/2个较大数据,放进兄弟节点中,而后将中间数据存进父结点中,若没有父节点,则进行创建父节点并将中间那个数据放入
此时便完成了75的插入
我们在这里思考一下为什么要分裂时,要将中位数插到父亲呢?其实原因就是新增了一个兄弟节点,这样父亲多了一个孩子,那么还需要多一个关键字,这样才能保持孩子的数量比关键字数量多一个
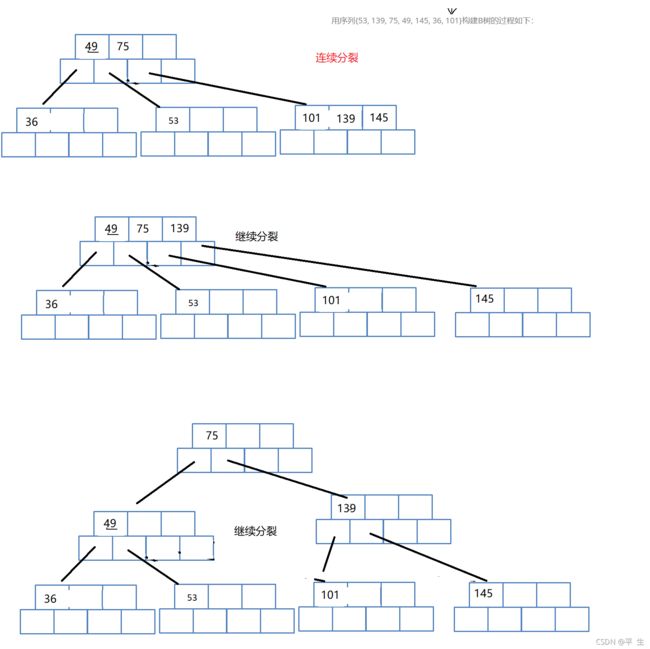
我们继续进行插入49,145,36
当我们插入49时,判断比53小,53后移,插到前面,插入145时,判断比139大,插到139后面,插入36时,,比49小,49,53后移,插到前面
此时节点中又满了,同上面一样,创建一个兄弟节点,将M/2,也就是53,放到兄弟节点中,将中位数,放到父亲节点中,完成插入
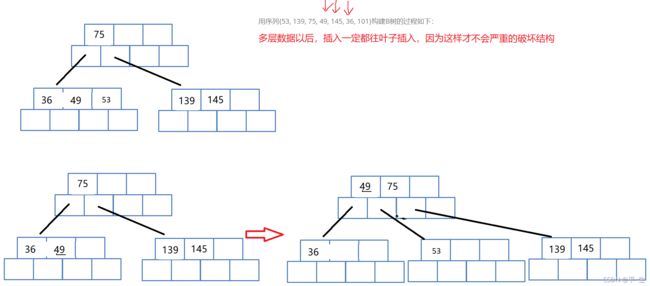
此时我们接着进行插入101
因为101比139小,所以139,145后移,101插到前面,此时节点满,我们向上面处理的一样,创建兄弟节点,145放到兄弟节点中,139放到父结点中,但此时父节点满了,依旧像上面一样,创建兄弟节点,139放到兄弟节点中,75放到新创建的父节点中,注意,这里139移动时也会连带着它的子树一起移动,此时便完成了插入
注意:当树拥有多层结点时,插入节点,要插入在叶子节点中,这样才能尽可能的保证规则不被打破
我们思考下B树是如何保证平衡的
1.B树的插入,仅有在满了的时候才会分裂出新节点,新节点与原结点都在同一层,也就是说他的新结点都是在同一层横向产生的
2.根节点分裂,才会增加高度,新增一层
也就是说B树是横向与向上生长的,天然平衡
而因为B树拥有这样独特的结构,所以其在大搜索时可以保证很快的效率,实际中,像文件系统或者数据库中使用的B树及其变形,索引数据一般M都很大,一般都会设置成1024,这也就说明其有如下的存储量
我们来看看其复杂度
其增删改查只与每个节点的有效数据量有关,想当与一个M分的结构,M叉树,所以其效率为O的以M为底的N的对数
B-树的插入实现
#pragma once
#include
using namespace std;
template
struct BTreeNode
{
// 孩子的数量比关键字的数量多一个
/*pair _kvs[M - 1];
BTreeNode* _subs[M];*/
// 空出一个空间,方便分裂,方便我们插入以后在分裂
pair _kvs[M];//关键字域
BTreeNode* _subs[M+1];//孩子指针域
BTreeNode* _parent;//父指针
size_t _kvSize;//关键字个数
BTreeNode()//初始化
:_kvSize(0)
, _parent(nullptr)
{
for (size_t i = 0; i < M+1; ++i)
{
_subs[i] = nullptr;
}
}
};
template
class BTree
{
typedef BTreeNode Node;//重命名
public:
// 第i个key的左孩子是subs[i]
// 第i个key的右孩子是subs[i+1]
pair Find(const K& key)//查找
{
Node* parent = nullptr;//初始化父节点
Node* cur = _root;//初始化cur结点
while (cur)//循环cur
{
size_t i = 0;//初始化i,也就是目标的下标
while (i < cur->_kvSize) // 如果M比较大,这里应该改一改换成二分查找会快一些
{
if (cur->_kvs[i].first < key) // key大于当前位置key,往右找
++i;
else if (cur->_kvs[i].first > key) // key小于当前位置key,就往左孩子去找
break;
else
return make_pair(cur, i);//找到
}
parent = cur;//向下查找,上面++过就去右孩子,没++就去左孩子
cur = cur->_subs[i];
}
// 没有找到
return make_pair(parent, -1);
}
// 往cur里面插入一个kv和sub
void InsertKV(Node* cur, const pair& kv, Node* sub)
{
// 将kv找到合适的位置插入进去
int i = cur->_kvSize - 1;//i置为节点末尾,为了方便向后移动数据
for (; i >= 0; )
{
if (cur->_kvs[i].first < kv.first)//判断插入的值大于节点中的值
{
break;//将i停在这里
}
else//判断出要插入的值较小
{
//kv[i]往后挪动,kv[i]的右孩子也挪动
cur->_kvs[i + 1] = cur->_kvs[i];
cur->_subs[i + 2] = cur->_subs[i + 1];
--i;
}
}
cur->_kvs[i+1] = kv;//插入结点
cur->_subs[i+2] = sub;//插入对应的孩子节点
cur->_kvSize++;//增加关键字个数
if (sub)//当结点成功插入
{
sub->_parent = cur;//链接到原来节点
}
}
bool Insert(const pair& kv)//插入
{
if (_root == nullptr)//当没有结点时新创建一个节点
{
_root = new Node;
_root->_kvs[0] = kv;
_root->_kvSize = 1;
return true;
}
pair ret = Find(kv.first);//查找,成功则返回目标指针,失败则返回其父节点的指针
// 已经有了,不能插入 (当前如果允许插入就是mutil版本)
if (ret.second >= 0)//当数字个数已经有了
{
return false;//插入失败
}
// 往cur节点中插入一个newkv和sub
// 1、如果cur没满就结束
// 2、如果满了就分裂,分裂出兄弟以后,往父亲插入一个关键字和孩子,再满还要继续分裂
// 3、最坏的情况就是分裂到根,原来根分裂,产生出一个新的根,就结束了
// 也就是说,我们最多分裂高度次
Node* cur = ret.first;//初始化cur为父节点
pair newkv = kv;//初始化newkv为原来的kv
Node* sub = nullptr;//初始化子指针
while (1)//建立死循环
{
InsertKV(cur, newkv, sub); //插入结点与关键字
// 1、如果cur没满就结束
if (cur->_kvSize < M)
{
return true;
}
else // 2、满了,需要分裂
{
// 分裂出一个兄弟节点
Node* newnode = new Node;
// 1、拷贝右半区间给分裂的兄弟节点
//
int mid = M / 2;//初始化mid
int j = 0;//初始化j为关键字头
int i = mid + 1;//初始化i为第一个需要拷贝的位置
newkv = cur->_kvs[mid];//将中位数存到newkv中
cur->_kvs[mid] = pair();//空出cur
for (; i < M; ++i)
{
newnode->_kvs[j] = cur->_kvs[i];//结点右半边拷贝到新的兄弟节点
cur->_kvs[i] = pair();//置空cur
newnode->_subs[j] = cur->_subs[i];//子节点也拷过去
cur->_subs[i] = nullptr;//子指针置空
if (newnode->_subs[j])//当兄弟节点有子节点时
{
newnode->_subs[j]->_parent = newnode;//链接子节点与兄弟节点
}
j++;//向后移动
newnode->_kvSize++;//兄弟节点的size++
}
// 还剩最后一个右孩子
newnode->_subs[j] = cur->_subs[i];///将子节点链到兄弟节点中
if (newnode->_subs[j])//当兄弟结点有子节点
{
newnode->_subs[j]->_parent = newnode;
}
cur->_kvSize = cur->_kvSize - newnode->_kvSize - 1;//更新旧节点中的size
// 1、如果cur没有父亲,那么cur就是根,产生新的根
// 2、如果cur有父亲,那么就要转换成往cur的父亲中插入一个key和一个孩子newnode
if (cur->_parent == nullptr)//当结点无父亲
{
_root = new Node;//创建新结点
_root->_kvs[0] = newkv;//初始化kv
_root->_subs[0] = cur;//初始化左子节点
_root->_subs[1] = newnode;//初始化右子节点
cur->_parent = _root;//链接左树
newnode->_parent = _root;//链接右树
_root->_kvSize = 1;//size置1
return true;
}
else
{
// 往父亲去插入newkv和newnode,转换成迭代逻辑
sub = newnode;//向上迭代
cur = cur->_parent;
}
}
} B树的删除与遍历
对于B树的删除与遍历,我们不进行实现,只在这里叙述原理
删除
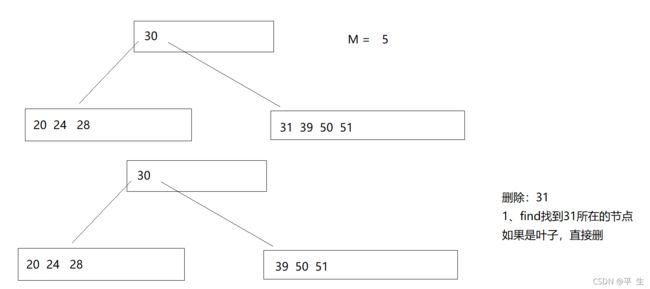
假设要删的在叶子节点上,我们只需要直接进行删除即可,对树的结构影响不大
而当我们需要删除非叶子结点时,我们需要向孩子借结点,借完孩子不够,孩子就继续向孙子借,直到叶子节点
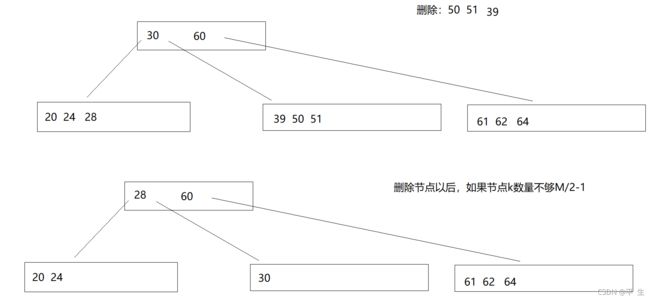
当我们删除删到某一个节点中无数据了时,我们需要让其向两边借结点,尽量不能使叶子节点减少
而当我们一直在删,两边也无法借结点了,此时我们将两个叶子节点合并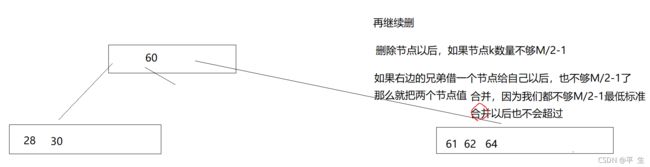
这便是删除的基本逻辑
遍历
因为我们的搜索树前序与后续意义不大,所以我们基本都是中序遍历,不过在B树中,中序遍历不能像之前那样左根右去遍历,因为对于B树而言,不是二叉树,而是M叉树,如果像之前那么遍历,会多遍历右子树,所以我们遍历方式为左根左根左根....右,只遍历最后的右,这样就将B树顺序的遍历了出来
B+树
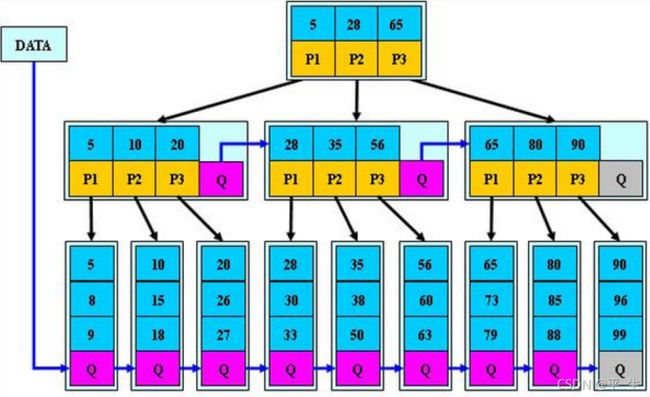
B+树其实就是在B树的基础上进行改进B+树的规则基本和B树一样,除了以下几点变化1.每个节点中,孩子的数量与关键字的数量一样(ps:相当于 在B树中取消掉了最左边的左孩子)2.为所有叶子节点增加一个链指针3.所有关键字都在叶子节点出现(ps:所有值(kv)都存在叶子,非叶子只能存k,目标是方便找到kv所在的叶子,每个节点存的就是孩子中的最小值)如果是kv结构,非叶子只存k,叶子存kv如果是k结构,非叶子存k,叶子存k但所有的值都存在叶子
总结:kv结构的B+树的规则与优点
1.根节点k和孩子的数量都是[1,M]
2.非根节点kv和孩子的数量都是[M/2,M]
3.每个节点中关键字数量与孩子数量一致
4.一个节点中关键字按升序排列,且sub[i]中所有值的大小在k[i]与k[i+1]之间
5.所有kv都要存在叶子中,非叶子只存k,父亲存的k是所有孩子的最小值
6.所有叶子被链接起来,还有一个指针指向第一个叶子节点
优缺点:
a.B+树找任何一个值都会走到叶子节点
b.B+的遍历很方便,因为所有值都在叶子,叶子是链接起来的
B+树的插入
B+树的插入大体和B树是一样的,不过还有细微的差别
当我们将53,139,75,49插入时,同我们B树一样,大小去排,大的在下,小的在上 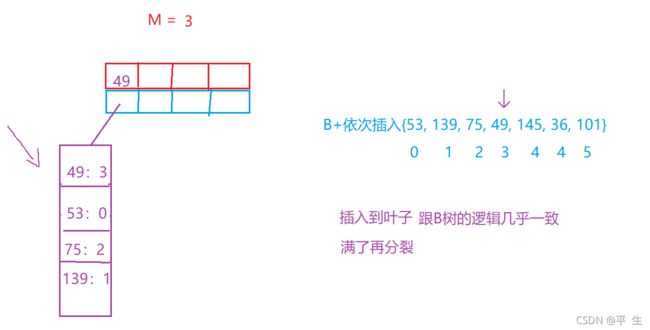
此时139插入之后我们就需要进行分裂了,那么B+树是如何进行分裂的呢?
我们B+树的分裂与B树略有不同,同样的,开辟兄弟节点,将后M/2个数据放到兄弟节点中,而后不同的是,B+树不需要将中位数给到父亲,取而代之的是将第一个元素给到父亲
B*树(了解)
B树的应用
索引
B- 树最常见的应用就是用来做索引 。索引通俗的说就是为了方便用户快速找到所寻之物,比如:书籍目录可以让读者快速找到相关信息,hao123 网页导航网站,为了让用户能够快速的找到有价值的分类网站,本质上就是互联网页面中的索引结构。MySQL 官方对索引的定义为: 索引 (index) 是帮助 MySQL 高效获取数据的数据结构,简单来说:索引就是数 据结构 。当数据量很大时,为了能够方便管理数据,提高数据查询的效率,一般都会选择将数据保存到数据库,因此数据库不仅仅是帮助用户管理数据,而且数据库系统还维护着满足特定查找算法的数据结构,这些数据结构以某种方式引用数据,这样就可以在这些数据结构上实现高级查找算法,该数据结构就是索引。
MyISAM
MyISAM 引擎是 MySQL5.5.8 版本之前默认的存储引擎,不支持事物,支持全文检索,使用 B+Tree 作为索引结构,叶节点的data 域存放的是数据记录的地址,其结构如下:
我们是可以利用两个语句分别查到数据的
虽然这两个sql语句查到的都是一组值,但是他们的效率是完全不一样的
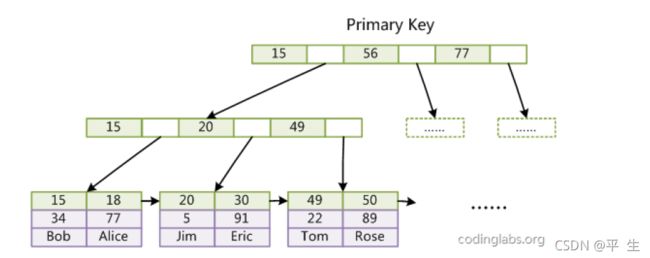
第一个sql时主键,也就是利用B+树key进行查找,非常快
第二个sql是非主键查找,只能全表扫描,非常慢
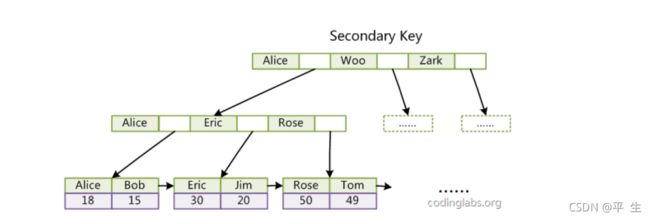
那么此时如果我们经常是使用anme查找,怎么办?我们可以对name字段建立一个索引,本质上建立索引就是再建立一个B+树,key是name
同样也是一棵 B+Tree , data 域保存数据记录的地址。因此, MyISAM 中索引检索的算法为首先按照 B+Tree 搜索算法搜索索引,如果指定的Key 存在,则取出其 data 域的值,然后以 data 域的值为地址,读取相应数据记录。 MyISAM 的索引方式也叫做 “ 非聚集索引 ” 的
InnoDB
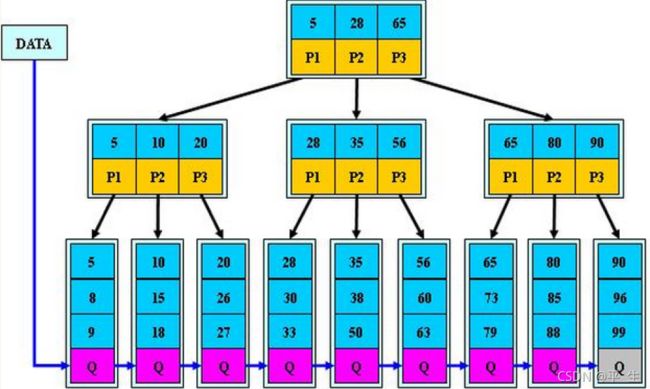
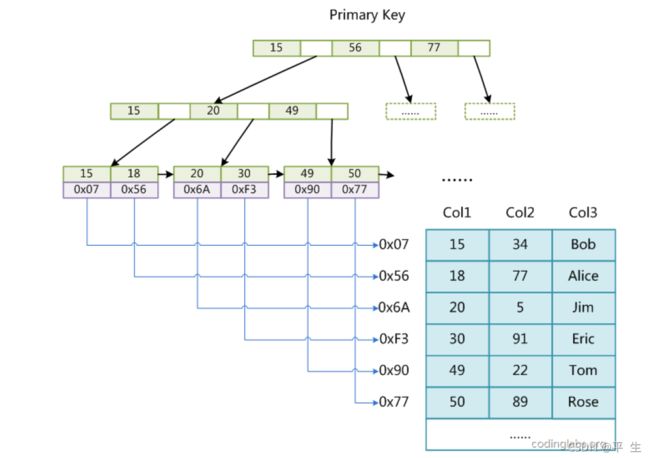
InnoDB 存储引擎支持事务 ,其设计目标主要面向在线事务处理的应用,从 MySQL 数据库 5.5.8 版本开始, InnoDB 存储引擎是默认的存储引擎 。 InnoDB 支持 B+ 树索引、全文索引、哈希索引。但 InnoDB 使用 B+Tree作为索引结构时,具体实现方式却与MyISAM 截然不同。第一个区别是 InnoDB 的数据文件本身就是索引文件 。 MyISAM 索引文件和数据文件是分离的,索引文件仅 保存数据记录的地址 。而 InnoDB 索引,表数据文件本身就是按 B+Tree 组织的一个索引结构,这棵树的叶节 点 data 域保存了完整的数据记录 。这个索引的 key 是数据表的主键,因此 InnoDB 表数据文件本身就是主索引。
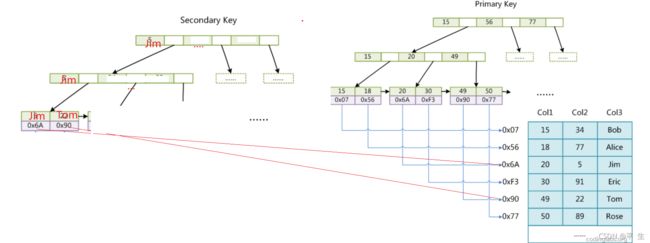
上图是 InnoDB 主索引 (同时也是数据文件)的示意图,可以看到 叶节点包含了完整的数据记录,这种索引 叫做聚集索引 。因为 InnoDB 的数据文件本身要按主键聚集,所以 InnoDB 要求表必须有主键 ( MyISAM 可以没有),如果没有显式指定,则 MySQL 系统会自动选择一个可以唯一标识数据记录的列作为主键 , 如果不存 在这种列,则 MySQL 自动为 InnoDB 表生成一个隐含字段作为主键,这个字段长度为 6 个字节,类型为长整 形 。第二个区别是 InnoDB 的辅助索引 data 域存储相应记录主键的值而不是地址 , 所有辅助索引都引用主键作为data域。
聚集索引这种实现方式使得按主键的搜索十分高效 ,但是 辅助索引搜索需要检索两遍索引:首先检索辅助索 引获得主键,然后用主键到主索引中检索获得记录。
结尾问题