CTF-Crypto 第二天-DES加密算法原理学习
文章目录
- DES算法简介
- DES算法流程
-
- 迭代加密
- 费斯妥函数(F函数)
- 密钥调度
- 混淆与扩散
DES算法简介
数据加密标准(Data Encryption Standard,缩写DES)是一种对称加密算法,也是一种分组加密算法。
- 对称加密指的是在加密和机密时使用同一个密钥的加密算法,加密算法可以被公开,发送和接收双方要事先得到同一个密钥。
常见的对称加密算法有AES、ChaCha20、3DES、Salsa20、DES、Blowfish、IDEA、RC5、RC6、Camellia以及我国的SM1。 - 分组加密指的是该算法将明文分成多个等长的模块(block),使用确定的算法和对称密钥对每组分别加密解密。
比如DES每次接收 8 个字节的明文数据也就是64-bit的数据,只需要将我们的明文分割成多个 8 字节大小的快,理论上就可以对任意长度的明文进行加密。 如果明文长度不是 8 的倍数,那么就需要进行填充。填充方式有PKCS5/PKCS7.
DES算法流程
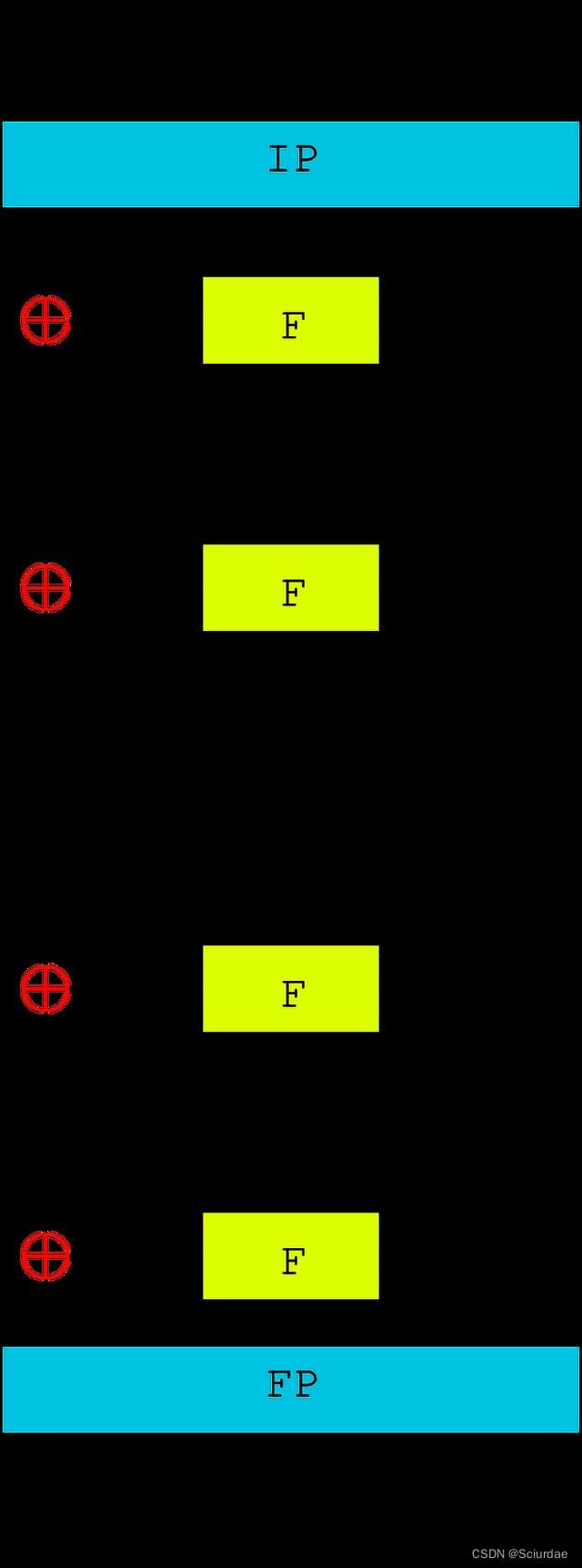
DES算法流程图:

source: https://www.youtube.com/watch?v=qkBisYq8iIs
从上图中可以看出DES算法的整体结构,有16个相同的处理过程,称为’回次’,并在首尾各有一次置换,IP和FP,(实际上FP为IP的反函数,即IP撤销FP的操作)。
从图中也可以发现,DES被分为了俩个部分,左边的是迭代加密,右边是密钥调度;接下来先分析一下迭代加密部分:
迭代加密
- 步骤一:将输入的64-bit明文做一个IP置换,仍然得到64bit的数组
- 步骤二: 将64-bit的明文数组拆分成左右俩个32-bit的数组
-步骤三: 进行迭代,每一轮迭代都是接收一组 L , R; 然后返回 L’ ,R’ ;作为下一轮迭代的L,R。其中的F函数被称为抡函数,是整个DES算法的核心,功能是以一个子密钥加密32-bit的信息。 - 步骤四:利用密钥调度生成的16个子密钥,执行步骤三16次。
- 步骤五:将最终的R和L拼接起来,在进行一次FP置换,得到密文。
费斯妥函数(F函数)
- 步骤一:用扩张置换(图中的E)将32-bit的半块扩展到48-bit 。
- 步骤二:与子密钥进行疑惑操作(子密钥的生成见密钥调度)
- 步骤三:S盒-在和子密钥进行混合后,块被分为 8 个 6 位的块, 然后使用 置换盒,或称为S盒,进行处理。8个S盒的每一个都使用以查找表方式提供的非线性的变换将它的 6 个输入位变成 4 个输出位。 S盒 提供了DES的核心安全性–如果没有S盒,密码会是线性的,很容易破解
- 步骤四:置换-最后S盒的 32 个输出位利用固定的置换,"P置换"进行重组。
置换盒:(部分)
密钥调度
- 步骤一:从64-bit的主钥匙中经过PC1置换提取特定的56位,将其分为左、右两个半密钥,他们都是28-bit的布尔数组。
- 步骤二:将左、右俩个半密钥都左旋一定位数(左旋表在下方)有时候左旋1,有时候左旋2;
什么是左旋,就是循环左移,将整个数组往左移,左边弹出的东西补到最右边去。 - 步骤三: 将左、右俩个半密钥拼接起来,再做一个PC2置换,得到这一轮生成的子密钥,这个置换是从56-bit中提取特定的48-bit。所以每一轮都生成了一个48-bit 的子密钥。
- 步骤四:重复步骤二和步骤三,一共16次,得到16个48-bit的子密钥。
问题:为什么在PC1置换中,要提取特定的56bit?
原64-bit中每8-bit就有1-bit是用于奇偶校验的,为了避免在数据传输过程中出现错误。这也是因为DES的设计考虑了历史上的一种电话系统,它要求每个字节都有奇数个’1’位,以确保数据传输的可靠性。
混淆与扩散
在费斯妥函数(F函数),S盒,P置换和E扩张各自满足了克劳德·香农在1940年代提出的实用密码所需的必要条件,“混淆与扩散”。
在密码学当中,混淆(confusion)与扩散(diffusion)是设计密码学算法的两种主要方法。这样的定义最早出现在克劳德·香农1945年的论文《密码学的数学理论》当中。
- 在克劳德·香农的定义之中,混淆主要是用来使密文和对称式加密方法中密钥的关系变得尽可能的复杂;而扩散则主要是用来使用明文和密文的关系变得尽可能的复杂,明文中任何一点小更动都会使得密文有很大的差异。
- 混淆用于掩盖明文与密文之间的关系。这可以挫败通过研究密文以获取冗余度和统计模式的企图。做到这一点最容易的方法是“代替”。
- 扩散通过将明文冗余度分散到密文中使之分散开来。即将单个明文或密钥位的影响尽可能扩大到更多的密文中去。产生扩散最简单的方法是换位(置换)。
基于python的DES加解密代码:
from functools import reduce
import numpy as np
# 整数转二进制数组,指定位长 n,大端序
def int2bin(a, n):
assert 0<=n and a < 2**n
res = np.zeros(n, dtype = int)
for x in range(n):
res[n-x-1] = a % 2
a = a // 2
return res.tolist()
assert int2bin(0x1a, 10) == [0, 0, 0, 0, 0, 1, 1, 0, 1, 0]
# 二进制数组转整数,大端序
def bin2int(a):
return reduce(lambda x,y: x*2+y, a)
assert bin2int([0, 0, 0, 0, 0, 1, 1, 0, 1, 0]) == 0x1a
# 循环左移off位
def leftRotate(a, off):
return a[off:] + a[:off]
assert leftRotate([0, 1, 0, 1, 1], 2) == [0, 1, 1, 0, 1]
# 异或
def binXor(a, b):
assert len(a) == len(b)
return [x^y for x, y in zip(a, b)]
assert binXor([1, 1, 0, 1], [0, 1, 1, 0]) == [1, 0, 1, 1]
# 初始置换
def IP(a):
ip = [58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7]
return [a[x-1] for x in ip]
testM = [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1]
assert IP(testM) == [1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0]
# 最终置换
def FP(a):
fp = [40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25]
return [a[x-1] for x in fp]
# 选择置换1
# 从64位输入密钥中选择56位,分为左右两个28位半密钥
def PC1(key):
pc1_l = [57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36]
pc1_r = [63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4]
return [key[x-1] for x in pc1_l], [key[x-1] for x in pc1_r]
testKey = [0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1]
testL, testR = PC1(testKey)
assert testL + testR == [1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1]
# 选择置换2
# 从56位的密钥中选取48位子密钥
def PC2(key):
assert len(key) == 56
pc2 = [14, 17, 11, 24, 1, 5,
3, 28, 15, 6, 21, 10,
23, 19, 12, 4, 26, 8,
16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55,
30, 40, 51, 45, 33, 48,
44, 49, 39, 56, 34, 53,
46, 42, 50, 36, 29, 32]
return [key[x-1] for x in pc2]
# 子密钥生成算法,由一个64位主密钥导出16个48位子密钥
def keyGen(key):
assert len(key) == 64
l, r = PC1(key)
off = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
res = []
for x in range(16):
l = leftRotate(l, off[x])
r = leftRotate(r, off[x])
res.append(PC2(l + r))
return res
assert keyGen(testKey)[-1] == [1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1]
# S盒变换,输入48位,输出32位
def S(a):
assert len(a) == 48
S_box = [[14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7,
0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8,
4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0,
15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13],
[15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10,
3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5,
0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15,
13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9],
[10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8,
13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1,
13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7,
1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12],
[7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15,
13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9,
10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4,
3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14],
[2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9,
14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6,
4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14,
11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3],
[12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11,
10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8,
9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6,
4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13],
[4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1,
13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6,
1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2,
6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12],
[13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7,
1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2,
7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8,
2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11]]
a = np.array(a, dtype=int).reshape(8, 6)
res = []
for i in range(8):
# 用 S_box[i] 处理6位a[i],得到4位输出
p = a[i]
r = S_box[i][bin2int([p[0], p[5], p[1], p[2], p[3], p[4]])]
res.append(int2bin(r, 4))
res = np.array(res).flatten().tolist()
assert len(res) == 32
return res
# 扩张置换,将32位的半块扩展到48位
def Expand(a):
assert len(a) == 32
e = [32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1]
return [a[x-1] for x in e]
# P置换
def P(a):
assert len(a) == 32
p = [16, 7, 20, 21,
29, 12, 28, 17,
1, 15, 23, 26,
5, 18, 31, 10,
2, 8, 24, 14,
32, 27, 3, 9,
19, 13, 30, 6,
22, 11, 4, 25]
return [a[x-1] for x in p]
# F函数,用于处理一个半块
def Feistel(a, subKey):
assert len(a) == 32
assert len(subKey) == 48
t = binXor(Expand(a), subKey)
t = S(t)
t = P(t)
return t
def goRound(l, r, subKey):
return r, binXor(l, Feistel(r, subKey))
def DES(plain, key, method):
subkeys = keyGen(int2bin(key, 64))
if method == 'decrypt':
subkeys = subkeys[::-1]
m = IP(int2bin(plain, 64))
l, r = np.array(m, dtype=int).reshape(2, -1).tolist()
for i in range(16):
l, r = goRound(l, r, subkeys[i])
return bin2int(FP(r + l))
print(hex(DES(0x11aabbccddeeff01, 0xcafababedeadbeaf, 'encrypt')))
# 0x2973a7e54ec730a3
print(hex(DES(0x2973a7e54ec730a3, 0xcafababedeadbeaf, 'decrypt')))
# 0x11aabbccddeeff01
代码来源至https://www.ruanx.net/des/,作者:RUAN XINGZHI
文献参考:
https://www.youtube.com/watch?v=qkBisYq8iIs&t=1155s
https://www.ruanx.net/des/
https://zh.wikipedia.org/wiki/%E8%B3%87%E6%96%99%E5%8A%A0%E5%AF%86%E6%A8%99%E6%BA%96