羊城杯-2023-Crypto
文章目录
- Danger_RSA
-
-
- 题目描述:
- 题目分析:
-
- Easy_3L
-
-
- 题目描述:
- 题目分析:
-
- XOR贯穿始终
-
-
- 题目描述:
- 题目分析:
-
- MCeorpkpleer
-
-
- 题目描述:
- 题目分析:
-
- SigninCrypto
-
-
- 题目描述:
- 题目分析:
-
- esyRSA
-
-
- 题目描述:
- 题目分析:
-
- 浅记一下
Danger_RSA
题目描述:
from Crypto.Util.number import *
m = bytes_to_long(flag)
def get_key(a, nbit):
assert a >= 2
while True:
X = getRandomInteger(nbit // a)
s = getRandomRange(pow(2, a ** 2 - a + 4), pow(2, a ** 2 - a + 5))
p = X ** a + s
if isPrime(p):
return (p, s)
p, s = get_key(a, 1024)
q, t = get_key(a, 1024)
N = p * q
e = s * t
c = pow(m, e, N)
print("N =", N)
print("e =", e)
print("c =", c)
N = 20289788565671012003324307131062103060859990244423187333725116068731043744218295859587498278382150779775620675092152011336913225797849717782573829179765649320271927359983554162082141908877255319715400550981462988869084618816967398571437725114356308935833701495015311197958172878812521403732038749414005661189594761246154666465178024563227666440066723650451362032162000998737626370987794816660694178305939474922064726534186386488052827919792122844587807300048430756990391177266977583227470089929347969731703368720788359127837289988944365786283419724178187242169399457608505627145016468888402441344333481249304670223
e = 11079917583
c = 13354219204055754230025847310134936965811370208880054443449019813095522768684299807719787421318648141224402269593016895821181312342830493800652737679627324687428327297369122017160142465940412477792023917546122283870042482432790385644640286392037986185997262289003477817675380787176650410819568815448960281666117602590863047680652856789877783422272330706693947399620261349458556870056095723068536573904350085124198592111773470010262148170379730937529246069218004969402885134027857991552224816835834207152308645148250837667184968030600819179396545349582556181916861808402629154688779221034610013350165801919342549766
题目分析:
e . n b i t s ( ) = 34 , 可知 s , t 分别为 17 b i t s , a 2 − a + 5 = 17 = > a = 4 ( 可以自己去测试这个结果 ) e.nbits() = 34,可知s,t分别为17bits,a^2 - a + 5 = 17=>a = 4 \ (可以自己去测试这个结果) e.nbits()=34,可知s,t分别为17bits,a2−a+5=17=>a=4 (可以自己去测试这个结果)
简化一下 p = X 1 4 + s q = X 2 4 + t s , t 可通过 s a g e 中的 d i v i s i o n 函数分解得到 ( 通过是否为 17 b i t s 来进行取舍 ) ⇒ s , t 较小,那么 X 1 X 2 = i r o o t ( n , 4 ) [ 0 ] 又 n = ( X 1 4 + s ) ∗ ( X 2 4 + t ) 联立两个方程求解得到 X 1 , X 2 , 那么 p , q 也就出来了 简化一下\\ p = X_1 ^ {4} + s\\ q = X_2 ^ {4} + t\\ s,t可通过sage中的division函数分解得到\\(通过是否为17bits来进行取舍)\\ \Rightarrow s,t较小,那么X_1X_2 = iroot(n,4)[0]\\ 又n = (X_1 ^ {4} + s) * (X_2 ^ {4} + t)\\ 联立两个方程求解得到X_1,X_2,那么p,q也就出来了 简化一下p=X14+sq=X24+ts,t可通过sage中的division函数分解得到(通过是否为17bits来进行取舍)⇒s,t较小,那么X1X2=iroot(n,4)[0]又n=(X14+s)∗(X24+t)联立两个方程求解得到X1,X2,那么p,q也就出来了
# sage
from gmpy2 import *
from Crypto.Util.number import *
n = 20289788565671012003324307131062103060859990244423187333725116068731043744218295859587498278382150779775620675092152011336913225797849717782573829179765649320271927359983554162082141908877255319715400550981462988869084618816967398571437725114356308935833701495015311197958172878812521403732038749414005661189594761246154666465178024563227666440066723650451362032162000998737626370987794816660694178305939474922064726534186386488052827919792122844587807300048430756990391177266977583227470089929347969731703368720788359127837289988944365786283419724178187242169399457608505627145016468888402441344333481249304670223
e = 11079917583
c = 13354219204055754230025847310134936965811370208880054443449019813095522768684299807719787421318648141224402269593016895821181312342830493800652737679627324687428327297369122017160142465940412477792023917546122283870042482432790385644640286392037986185997262289003477817675380787176650410819568815448960281666117602590863047680652856789877783422272330706693947399620261349458556870056095723068536573904350085124198592111773470010262148170379730937529246069218004969402885134027857991552224816835834207152308645148250837667184968030600819179396545349582556181916861808402629154688779221034610013350165801919342549766
# a = divisors(e)
# for i in a:
# if i.nbits() == 17 and (e // i).nbits() == 17:
# print(i)
# print(e // i)
r,s = 91903,120561
X1X2 = int(iroot(n,4)[0])
# X1,X2 = var('X1 X2')
# f1 = X1 * X2 == X1X2
# f2 = (X1 ** 4 + s) * (X2 ** 4 + t) == n
# print(solve([f1,f2],[X1,X2]))
X1 = 44416071018427916652440592614276227563515579156219730344722242565477265479486
X2 = 47783641287938625512681830427927501009821495321018170621907812035456872958654
p = X1 ** 4 + r
q = X2 ** 4 + s
可以发现gcd(e,p - 1)与gcd(e,q-1)都不为1,(e,p-1) = 49,(e,q-1) = 3。又p,q长度为1024,比flag大得多,可直接进行在模p或q下的有限域开方,之后再遍历即可得到flag
# 承接上面代码
d = invert(e // 3,(q - 1))
m_3 = pow(c,d,q)
e = 3
R.<x> = Zmod(q)[]
f=x^e-m_3
mps=f.monic().roots()
for i in mps:
flag=long_to_bytes(int(i[0]))
if b'CTF' in flag:
print(flag)
# b'DASCTF{C0nsTruct!n9_Techn1qUe2_f0r_RSA_Pr1me_EnC2ypt10N}'
拓展:
AMM算法求解:
import random
import time
from tqdm import tqdm
from Crypto.Util.number import *
# About 3 seconds to run
def AMM(o, r, q):
start = time.time()
print('\n----------------------------------------------------------------------------------')
print('Start to run Adleman-Manders-Miller Root Extraction Method')
print('Try to find one {:#x}th root of {} modulo {}'.format(r, o, q))
g = GF(q)
o = g(o)
p = g(random.randint(1, q))
while p ^ ((q-1) // r) == 1:
p = g(random.randint(1, q))
print('[+] Find p:{}'.format(p))
t = 0
s = q - 1
while s % r == 0:
t += 1
s = s // r
print('[+] Find s:{}, t:{}'.format(s, t))
k = 1
while (k * s + 1) % r != 0:
k += 1
alp = (k * s + 1) // r
print('[+] Find alp:{}'.format(alp))
a = p ^ (r**(t-1) * s)
b = o ^ (r*alp - 1)
c = p ^ s
h = 1
for i in range(1, t):
d = b ^ (r^(t-1-i))
if d == 1:
j = 0
else:
print('[+] Calculating DLP...')
j = - discrete_log(d, a)
print('[+] Finish DLP...')
b = b * (c^r)^j
h = h * c^j
c = c^r
result = o^alp * h
end = time.time()
print("Finished in {} seconds.".format(end - start))
print('Find one solution: {}'.format(result))
return result
def onemod(p,r):
t=random.randint(2,p)
while pow(t,(p-1)//r,p)==1:
t=random.randint(2,p)
return pow(t,(p-1)//r,p)
def solution(p,root,e):
while True:
g=onemod(p,e)
may=[]
for i in tqdm(range(e)):
may.append(root*pow(g,i,p)%p)
if len(may) == len(set(may)):
return may
def solve_in_subset(ep,p):
cp = int(pow(c,inverse(int(e//ep),p-1),p))
com_factors = []
while GCD(ep,p-1) !=1:
com_factors.append(GCD(ep,p-1))
ep //= GCD(ep,p-1)
com_factors.sort()
cps = [cp]
for factor in com_factors:
mps = []
for cp in cps:
mp = AMM(cp, factor, p)
mps += solution(p,mp,factor)
cps = mps
for each in cps:
assert pow(each,e,p)==c%p
return cps
n = 20289788565671012003324307131062103060859990244423187333725116068731043744218295859587498278382150779775620675092152011336913225797849717782573829179765649320271927359983554162082141908877255319715400550981462988869084618816967398571437725114356308935833701495015311197958172878812521403732038749414005661189594761246154666465178024563227666440066723650451362032162000998737626370987794816660694178305939474922064726534186386488052827919792122844587807300048430756990391177266977583227470089929347969731703368720788359127837289988944365786283419724178187242169399457608505627145016468888402441344333481249304670223
e = 11079917583
p = 3891889986375336330559716098591764128742918441309724777337583126578227827768865619689858547513951476952436981068109005313431255086775128227872912287517417948310766208005723508039484956447166240210962374423348694952997002274647622939970550008327647559433222317977926773242269276334110863262269534189811138319
q = 5213351003420231819415242686664610206224730148063270274863722096379841592931572096469136339538500817713355302889731144789372844731378975059329731297860686270736540109105854515590165681366189003405833252270606896051264517339339578167231093908235856718285980689179840159807651185918046198419707669304960745217
c = 13354219204055754230025847310134936965811370208880054443449019813095522768684299807719787421318648141224402269593016895821181312342830493800652737679627324687428327297369122017160142465940412477792023917546122283870042482432790385644640286392037986185997262289003477817675380787176650410819568815448960281666117602590863047680652856789877783422272330706693947399620261349458556870056095723068536573904350085124198592111773470010262148170379730937529246069218004969402885134027857991552224816835834207152308645148250837667184968030600819179396545349582556181916861808402629154688779221034610013350165801919342549766
ep = 49
eq = 3
m_p = solve_in_subset(49,p)
m_q = solve_in_subset(3,q)
for mpp in m_p:
for mqq in m_q:
m = crt([int(mpp),int(mqq)],[p,q])
flag = long_to_bytes(m)
if b'CTF' in flag:
print(flag)
break
# b'DASCTF{C0nsTruct!n9_Techn1qUe2_f0r_RSA_Pr1me_EnC2ypt10N}'
Easy_3L
题目描述:
from gmpy2 import *
from Crypto.Util.number import *
from secret import flag
m = bytes_to_long(flag)
def get_key():
p = getPrime(1400)
f = getRandomNBitInteger(1024)
while True:
q = getPrime(512)
if gcd(f, q) != 1:
continue
else:
break
h = (invert(f, p) * q) % p
return p, h
def encrypt1(m):
a = getPrime(250)
b = getRandomNBitInteger(240)
n = getPrime(512)
seed = m
s = [0] * 6
s[0] = seed
for i in range(1, 6):
s[i] = (s[i - 1] * a + b) % n
return s
def encrypt2(msg, p, h):
s = getRandomNBitInteger(512)
c = (s * h + msg) % p
return c
s = encrypt1(m)
print("S1 =", s[1])
print("S2 =", s[2])
print("S4 =", s[4])
print("S5 =", s[5])
p, h = get_key()
c = encrypt2(s[3], p, h)
print("p =", p)
print("h =", h)
print("c =", c)
# S1 = 28572152986082018877402362001567466234043851789360735202177142484311397443337910028526704343260845684960897697228636991096551426116049875141
# S2 = 1267231041216362976881495706209012999926322160351147349200659893781191687605978675590209327810284956626443266982499935032073788984220619657447889609681888
# S4 = 9739918644806242673966205531575183334306589742344399829232076845951304871478438938119813187502023845332528267974698273405630514228632721928260463654612997
# S5 = 9755668823764800147393276745829186812540710004256163127825800861195296361046987938775181398489372822667854079119037446327498475937494635853074634666112736
# p = 25886434964719448194352673440525701654705794467884891063997131230558866479588298264578120588832128279435501897537203249743883076992668855905005985050222145380285378634993563571078034923112985724204131887907198503097115380966366598622251191576354831935118147880783949022370177789175320661630501595157946150891275992785113199863734714343650596491139321990230671901990010723398037081693145723605154355325074739107535905777351
# h = 2332673914418001018316159191702497430320194762477685969994411366563846498561222483921873160125818295447435796015251682805613716554577537183122368080760105458908517619529332931042168173262127728892648742025494771751133664547888267249802368767396121189473647263861691578834674578112521646941677994097088669110583465311980605508259404858000937372665500663077299603396786862387710064061811000146453852819607311367850587534711
# c = 20329058681057003355767546524327270876901063126285410163862577312957425318547938475645814390088863577141554443432653658287774537679738768993301095388221262144278253212238975358868925761055407920504398004143126310247822585095611305912801250788531962681592054588938446210412897150782558115114462054815460318533279921722893020563472010279486838372516063331845966834180751724227249589463408168677246991839581459878242111459287
题目分析:
唉,前面h = (invert(f, p) * q) % p真的是,一直盯着这里看,没往后看,花了好多时间。唉,题目还是要先完整看下来啊。
进入正题
考点在c = (s * h + S[3]) % p这串
c = ( s ∗ h + S [ 3 ] ) % p S [ 3 ] = c − s ∗ h + k ∗ p 构造如下格 M = ( 2 512 c 1 h p ) ( 1 , − s , k ) ∗ M = ( 2 512 , − s , S [ 3 ] ) L L L 之后得到 S [ 3 ] , 之后直接 L C G 求解即可得到 f l a g c = (s * h + S[3]) \% p \\ S[3] = c - s * h + k * p\\ 构造如下格\\ \ \\ M = \begin{pmatrix} 2^{512}&&c\\ &1&h\\ &&p \end{pmatrix}\\ \ \\ (1,-s,k) * M = (2 ^ {512},-s,S[3])\\ \ \\ LLL之后得到S[3],之后直接LCG求解即可得到flag c=(s∗h+S[3])%pS[3]=c−s∗h+k∗p构造如下格 M= 25121chp (1,−s,k)∗M=(2512,−s,S[3]) LLL之后得到S[3],之后直接LCG求解即可得到flag
3L:
from Crypto.Util.number import *
from gmpy2 import *
p = 25886434964719448194352673440525701654705794467884891063997131230558866479588298264578120588832128279435501897537203249743883076992668855905005985050222145380285378634993563571078034923112985724204131887907198503097115380966366598622251191576354831935118147880783949022370177789175320661630501595157946150891275992785113199863734714343650596491139321990230671901990010723398037081693145723605154355325074739107535905777351
h = 2332673914418001018316159191702497430320194762477685969994411366563846498561222483921873160125818295447435796015251682805613716554577537183122368080760105458908517619529332931042168173262127728892648742025494771751133664547888267249802368767396121189473647263861691578834674578112521646941677994097088669110583465311980605508259404858000937372665500663077299603396786862387710064061811000146453852819607311367850587534711
c = 20329058681057003355767546524327270876901063126285410163862577312957425318547938475645814390088863577141554443432653658287774537679738768993301095388221262144278253212238975358868925761055407920504398004143126310247822585095611305912801250788531962681592054588938446210412897150782558115114462054815460318533279921722893020563472010279486838372516063331845966834180751724227249589463408168677246991839581459878242111459287
M = matrix(ZZ,[[2 ** 512,0,c],[0,1,h],[0,0,p]])
M = M.LLL()
S3 = abs(M[0][-1])
# 10700695166096094995375972320865971168959897437299342068124161538902514000691034236758289037664275323635047529647532200693311709347984126070052011571264606
LCG:
import gmpy2
from Crypto.Util.number import *
# 逆元求法
MMI = lambda A, n,s=1,t=0,N=0: (n < 2 and t%N or MMI(n, A%n, t, s-A//n*t, N or n),-1)[n<1] # 逆元计算
S1 = 28572152986082018877402362001567466234043851789360735202177142484311397443337910028526704343260845684960897697228636991096551426116049875141
S2 = 1267231041216362976881495706209012999926322160351147349200659893781191687605978675590209327810284956626443266982499935032073788984220619657447889609681888
S3 = 10700695166096094995375972320865971168959897437299342068124161538902514000691034236758289037664275323635047529647532200693311709347984126070052011571264606
S4 = 9739918644806242673966205531575183334306589742344399829232076845951304871478438938119813187502023845332528267974698273405630514228632721928260463654612997
S5 = 9755668823764800147393276745829186812540710004256163127825800861195296361046987938775181398489372822667854079119037446327498475937494635853074634666112736
s = [S1,S2,S3,S4,S5]
t = []
for i in range(4): # len(out) - 1
t.append(s[i+1]-s[i])
for i in range(1):
n = gmpy2.gcd(t[i+3] * t[i+1] - t[i+2] * t[i+2],t[i+2] * t[i] - t[i+1] * t[i+1])
inv = MMI(s[1] - s[0], n) % n
a = (s[2] - s[1]) * inv % n
b = (s[1] - a * s[0]) % n
inv_a = MMI(a, n)
seed = (s[0] - b) * inv_a % n
print(long_to_bytes(seed))
# b'DASCTF{NTRU_L0G_a6e_S1mpLe}'
XOR贯穿始终
题目描述:
自由和谐和谐富强公正友善爱国公正法治法治文明和谐自由法治自由法治平等公正友善公正公正民主法治自由公正敬业和谐富强公正友善爱国和谐平等平等友善敬业法治敬业和谐富强法治平等平等友善敬业公正公正公正友善敬业法治平等平等诚信自由公正自由平等友善敬业公正友善法治和谐和谐
【解码得到C0ngr4tulati0n5_y0u_fou^d_m3作为下面两个文件的密码】
from gmpy2 import gcd
from Crypto.Util.number import getPrime
from secret import enflag
p = getPrime(512)
q = getPrime(512)
n = q * p
phi = (p - 1) * (q - 1)
e = getPrime(17)
assert gcd(e, phi) == 1
# 以上信息生成了私钥文件,但文件被损坏了你能提取有用信息吗
c = pow(enflag, e, n)
print('c = ' + str(c))
'''
c = 91817924748361493215143897386603397612753451291462468066632608541316135642691873237492166541761504834463859351830616117238028454453831120079998631107520871612398404926417683282285787231775479511469825932022611941912754602165499500350038397852503264709127650106856760043956604644700201911063515109074933378818
'''
-----BEGIN PRIVATE KEY-----
MIICdwIBADANBgkqhkiG9w0BAQEFAASCAmEwggJdAgEAAoGBALmtMy+2uH1ZtbIL
SuiAukFthyQRH5mp7UmLyzZQkdg9zEP9/5tgffikQ7ytx5kHySHnazgAO1sOzmYE
N4Axlev6uafiP8B1Eij97v5VkYJ1I9e3mtBNheTbXKoT8op+ASQ1fQaF4A8UzLuW
eZeZI8JTH/SH+bolAK3kiZXDFdkTAgMBAAECgYEAl067LaC7Cvs2A5cMPhfYsESv
IgcKN1CwW4Sd3u8dSphhgu7TgyzIuvwxbuo2g1BC6WwKhaI6vGN+csfw6nh98GEn
/p3D0huNroAYvf/DRRB9UnHdttX7wB+Mv3P0RBDWHgBiCDVvHFuFUV78cIs0tnbn
jxjU07aPV2XRC3AfA2ECQQDqWUNPVg3i6vTyHCL7EGkbeUheYpAAfcKCQrxjc5+5
X6A+XtgHAA1JHwykPlCpHUOmlA85DJF1ejuoImzlgRLJAkEAytTCnQF+MN2r1gaA
UETZyj5qMYT7Th8zKEVVVJjDawLnuX4usJ2FyRnjCkk86U75QSJhw5mMc0QnG25u
Gz3++w==
-----END PRIVATE KEY-----
题目分析:
以上信息生成了私钥文件,但文件被损坏了你能提取有用信息吗
细节看这篇文章
至此可以得到n,e,p,q
标题XOR贯穿始终,rsa得到的m与C0ngr4tulati0n5_y0u_fou^d_m3异或即可得到flag
from gmpy2 import *
from Crypto.Util.number import *
c = 91817924748361493215143897386603397612753451291462468066632608541316135642691873237492166541761504834463859351830616117238028454453831120079998631107520871612398404926417683282285787231775479511469825932022611941912754602165499500350038397852503264709127650106856760043956604644700201911063515109074933378818
n = 0x00b9ad332fb6b87d59b5b20b4ae880ba416d8724111f99a9ed498bcb365091d83dcc43fdff9b607df8a443bcadc79907c921e76b38003b5b0ece660437803195ebfab9a7e23fc0751228fdeefe5591827523d7b79ad04d85e4db5caa13f28a7e0124357d0685e00f14ccbb9679979923c2531ff487f9ba2500ade48995c315d913
e = 0x10001
p = 0xea59434f560de2eaf4f21c22fb10691b79485e6290007dc28242bc63739fb95fa03e5ed807000d491f0ca43e50a91d43a6940f390c91757a3ba8226ce58112c9
q = 0xcad4c29d017e30ddabd606805044d9ca3e6a3184fb4e1f332845555498c36b02e7b97e2eb09d85c919e30a493ce94ef9412261c3998c7344271b6e6e1b3dfefb
phi = (p-1)*(q-1)
d = invert(e,phi)
m = pow(c,d,n)
mm = b'C0ngr4tulati0n5_y0u_fou^d_m3'
print(long_to_bytes(m ^ bytes_to_long(mm)))
# b'DASCTF{0e2874af5e422482378640e61d919e9a}'
MCeorpkpleer
题目描述:
from Crypto.Util.number import *
from secret import flag
def pubkey(list, m, w):
pubkey_list = []
for i in range(len(e_bin)):
pubkey_list.append(w * list[i] % m)
return pubkey_list
def e_cry(e, pubkey):
pubkey_list = pubkey
encode = 0
for i in range(len(e)):
encode += pubkey_list[i] * int(e[i]) % m
return encode
p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = getPrime(64)
m = bytes_to_long(flag)
c = pow(m, e, n)
e_bin = (bin(e))[2:]
list = [pow(3, i) for i in range(len(e_bin))]
m = getPrime(len(bin(sum(list))) - 1)
w = getPrime(64)
pubkey = pubkey(list, m, w)
en_e = e_cry(e_bin, pubkey)
print('p = {}\n'
'n = {}\n'
'c = {}\n'
'pubkey = {}\n'
'en_e = {}'.format((p >> 435) << 435, n, c, pubkey, en_e))
p = 139540788452365306201344680691061363403552933527922544113532931871057569249632300961012384092481349965600565669315386312075890938848151802133991344036696488204791984307057923179655351110456639347861739783538289295071556484465877192913103980697449775104351723521120185802327587352171892429135110880845830815744
n = 22687275367292715121023165106670108853938361902298846206862771935407158965874027802803638281495587478289987884478175402963651345721058971675312390474130344896656045501040131613951749912121302307319667377206302623735461295814304029815569792081676250351680394603150988291840152045153821466137945680377288968814340125983972875343193067740301088120701811835603840224481300390881804176310419837493233326574694092344562954466888826931087463507145512465506577802975542167456635224555763956520133324723112741833090389521889638959417580386320644108693480886579608925996338215190459826993010122431767343984393826487197759618771
c = 156879727064293983713540449709354153986555741467040286464656817265584766312996642691830194777204718013294370729900795379967954637233360644687807499775502507899321601376211142933572536311131955278039722631021587570212889988642265055045777870448827343999745781892044969377246509539272350727171791700388478710290244365826497917791913803035343900620641430005143841479362493138179077146820182826098057144121231954895739989984846588790277051812053349488382941698352320246217038444944941841831556417341663611407424355426767987304941762716818718024107781873815837487744195004393262412593608463400216124753724777502286239464
pubkey = [18143710780782459577, 54431132342347378731, 163293397027042136193, 489880191081126408579, 1469640573243379225737, 4408921719730137677211, 13226765159190413031633, 39680295477571239094899, 119040886432713717284697, 357122659298141151854091, 1071367977894423455562273, 3214103933683270366686819, 9642311801049811100060457, 28926935403149433300181371, 86780806209448299900544113, 260342418628344899701632339, 781027255885034699104897017, 2343081767655104097314691051, 7029245302965312291944073153, 21087735908895936875832219459, 63263207726687810627496658377, 189789623180063431882489975131, 569368869540190295647469925393, 1708106608620570886942409776179, 601827224419797931380408071500, 1805481673259393794141224214500, 893952418336266652976851386463, 2681857255008799958930554159389, 3523079163584485147344841221130, 1524252287869625983140881149316, 50264262166963219975822190911, 150792786500889659927466572733, 452378359502668979782399718199, 1357135078508006939347199154597, 4071405235524020818041597463791, 3169230503688232995231149877299, 462706308180869526799807117823, 1388118924542608580399421353469, 4164356773627825741198264060407, 3448085117999647764701149667147, 1299270151115113835209806487367, 3897810453345341505629419462101, 2648446157152195057994615872229, 3422845870014670444537026359650, 1223552407160181874717436564876, 3670657221480545624152309694628, 1966986461557807413563286569810, 1378466783231507511243038452393, 4135400349694522533729115357179, 3361215846199738142293703557463, 1038662335715384967987468158315, 3115987007146154903962404474945, 302975818554635252993570910761, 908927455663905758980712732283, 2726782366991717276942138196849, 3657854499533237101379593333510, 1928578295715881845245137486456, 1263242285705730806288591202331, 3789726857117192418865773606993, 2324195368467747797703678306905, 2450093503961328663664213663678, 2827787910442071261545819733997, 3960871129884299055190637944954, 2837628186769067706678271320788]
en_e = 31087054322877663244023458448558
题目分析:
len(e_bin) = 64(通过pubkey的长度得知),由此list便知道了
容易得知list的第一个就是w,w知道了那么m也就好知道了
list1 = []
for i in list:
list1.append(w * i)
print(list1)
# list1 = [18143710780782459577, 54431132342347378731, 163293397027042136193, 489880191081126408579, 1469640573243379225737, 4408921719730137677211, 13226765159190413031633, 39680295477571239094899, 119040886432713717284697, 357122659298141151854091, 1071367977894423455562273, 3214103933683270366686819, 9642311801049811100060457, 28926935403149433300181371, 86780806209448299900544113, 260342418628344899701632339, 781027255885034699104897017, 2343081767655104097314691051, 7029245302965312291944073153, 21087735908895936875832219459, 63263207726687810627496658377, 189789623180063431882489975131, 569368869540190295647469925393, 1708106608620570886942409776179, 5124319825861712660827229328537, 15372959477585137982481687985611, 46118878432755413947445063956833, 138356635298266241842335191870499, 415069905894798725527005575611497, 1245209717684396176581016726834491, 3735629153053188529743050180503473, 11206887459159565589229150541510419, 33620662377478696767687451624531257, 100861987132436090303062354873593771, 302585961397308270909187064620781313, 907757884191924812727561193862343939, 2723273652575774438182683581587031817, 8169820957727323314548050744761095451, 24509462873181969943644152234283286353, 73528388619545909830932456702849859059, 220585165858637729492797370108549577177, 661755497575913188478392110325648731531, 1985266492727739565435176330976946194593, 5955799478183218696305528992930838583779, 17867398434549656088916586978792515751337, 53602195303648968266749760936377547254011, 160806585910946904800249282809132641762033, 482419757732840714400747848427397925286099, 1447259273198522143202243545282193775858297, 4341777819595566429606730635846581327574891, 13025333458786699288820191907539743982724673, 39076000376360097866460575722619231948174019, 117228001129080293599381727167857695844522057, 351684003387240880798145181503573087533566171, 1055052010161722642394435544510719262600698513, 3165156030485167927183306633532157787802095539, 9495468091455503781549919900596473363406286617, 28486404274366511344649759701789420090218859851, 85459212823099534033949279105368260270656579553, 256377638469298602101847837316104780811969738659, 769132915407895806305543511948314342435909215977, 2307398746223687418916630535844943027307727647931, 6922196238671062256749891607534829081923182943793, 20766588716013186770249674822604487245769548831379]
# list0 = [18143710780782459577, 54431132342347378731, 163293397027042136193, 489880191081126408579, 1469640573243379225737, 4408921719730137677211, 13226765159190413031633, 39680295477571239094899, 119040886432713717284697, 357122659298141151854091, 1071367977894423455562273, 3214103933683270366686819, 9642311801049811100060457, 28926935403149433300181371, 86780806209448299900544113, 260342418628344899701632339, 781027255885034699104897017, 2343081767655104097314691051, 7029245302965312291944073153, 21087735908895936875832219459, 63263207726687810627496658377, 189789623180063431882489975131, 569368869540190295647469925393, 1708106608620570886942409776179, 601827224419797931380408071500, 1805481673259393794141224214500, 893952418336266652976851386463, 2681857255008799958930554159389, 3523079163584485147344841221130, 1524252287869625983140881149316, 50264262166963219975822190911, 150792786500889659927466572733, 452378359502668979782399718199, 1357135078508006939347199154597, 4071405235524020818041597463791, 3169230503688232995231149877299, 462706308180869526799807117823, 1388118924542608580399421353469, 4164356773627825741198264060407, 3448085117999647764701149667147, 1299270151115113835209806487367, 3897810453345341505629419462101, 2648446157152195057994615872229, 3422845870014670444537026359650, 1223552407160181874717436564876, 3670657221480545624152309694628, 1966986461557807413563286569810, 1378466783231507511243038452393, 4135400349694522533729115357179, 3361215846199738142293703557463, 1038662335715384967987468158315, 3115987007146154903962404474945, 302975818554635252993570910761, 908927455663905758980712732283, 2726782366991717276942138196849, 3657854499533237101379593333510, 1928578295715881845245137486456, 1263242285705730806288591202331, 3789726857117192418865773606993, 2324195368467747797703678306905, 2450093503961328663664213663678, 2827787910442071261545819733997, 3960871129884299055190637944954, 2837628186769067706678271320788]
# m = 5124319825861712660827229328537 - 601827224419797931380408071500
# print(m)
m = 4522492601441914729446821257037
w = 18143710780782459577
m = 4522492601441914729446821257037
简化一下: e _ b i n = b i n ( e ) = ( e 1 , e 2 , . . . e 64 ) p u b k e y = ( p u b 1 , p u b 2 , . . . , p u b 64 ) 其中 e i 均为 0 或 1 e n _ e ≡ p u b 1 ∗ e 1 + p u b 2 ∗ e 2 + . . . + p u b 64 ∗ e 64 ( m o d m ) ⇒ e n _ e = p u b 1 ∗ e 1 + p u b 2 ∗ e 2 + . . . + p u b 64 ∗ e 64 + k ∗ m 0 = p u b 1 ∗ e 1 + p u b 2 ∗ e 2 + . . . + p u b 64 ∗ e 64 − e n _ e + k ∗ m 构造如下格: M = ( 1 p u b 1 1 p u b 2 ⋱ ⋮ 1 p u b 64 1 e n _ e m ) ( e 1 , e 2 , . . . , e 64 , − 1 , k ) ∗ M = ( e 1 , e 2 , . . . , e 64 , − 1 , 0 ) 简化一下:\\ e\_bin = bin(e) = (e_1,e_2,...e_{64})\\ pubkey = (pub_1,pub_2,...,pub_{64})\\ 其中e_i均为0或1\\ en\_e \equiv pub_1 * e_1 + pub_2 * e_2 + ... + pub_{64} * e_{64} \pmod m\\ \Rightarrow en\_e = pub_1 * e_1+ pub_2 * e_2 + ... + pub_{64} * e_{64} + k * m\\ 0 = pub_1 * e_1+ pub_2 * e_2 + ... + pub_{64} * e_{64} -en\_e + k * m\\ \ \\ 构造如下格:\\ \ \\ M = \begin{pmatrix} 1&&&&&pub_1\\ &1&&&&pub_2\\ &&\ddots&&&\vdots\\&&&1&&pub_{64}\\ &&&&1&en\_e\\&&&&&m \end{pmatrix}\\ \ \\ (e_1,e_2,...,e_{64},-1,k) * M = (e_1,e_2,...,e_{64},-1,0)\\ 简化一下:e_bin=bin(e)=(e1,e2,...e64)pubkey=(pub1,pub2,...,pub64)其中ei均为0或1en_e≡pub1∗e1+pub2∗e2+...+pub64∗e64(modm)⇒en_e=pub1∗e1+pub2∗e2+...+pub64∗e64+k∗m0=pub1∗e1+pub2∗e2+...+pub64∗e64−en_e+k∗m 构造如下格: M= 11⋱11pub1pub2⋮pub64en_em (e1,e2,...,e64,−1,k)∗M=(e1,e2,...,e64,−1,0)
from Crypto.Util.number import *
from hashlib import md5
m = 4522492601441914729446821257037
pubkey = [18143710780782459577, 54431132342347378731, 163293397027042136193, 489880191081126408579, 1469640573243379225737, 4408921719730137677211, 13226765159190413031633, 39680295477571239094899, 119040886432713717284697, 357122659298141151854091, 1071367977894423455562273, 3214103933683270366686819, 9642311801049811100060457, 28926935403149433300181371, 86780806209448299900544113, 260342418628344899701632339, 781027255885034699104897017, 2343081767655104097314691051, 7029245302965312291944073153, 21087735908895936875832219459, 63263207726687810627496658377, 189789623180063431882489975131, 569368869540190295647469925393, 1708106608620570886942409776179, 601827224419797931380408071500, 1805481673259393794141224214500, 893952418336266652976851386463, 2681857255008799958930554159389, 3523079163584485147344841221130, 1524252287869625983140881149316, 50264262166963219975822190911, 150792786500889659927466572733, 452378359502668979782399718199, 1357135078508006939347199154597, 4071405235524020818041597463791, 3169230503688232995231149877299, 462706308180869526799807117823, 1388118924542608580399421353469, 4164356773627825741198264060407, 3448085117999647764701149667147, 1299270151115113835209806487367, 3897810453345341505629419462101, 2648446157152195057994615872229, 3422845870014670444537026359650, 1223552407160181874717436564876, 3670657221480545624152309694628, 1966986461557807413563286569810, 1378466783231507511243038452393, 4135400349694522533729115357179, 3361215846199738142293703557463, 1038662335715384967987468158315, 3115987007146154903962404474945, 302975818554635252993570910761, 908927455663905758980712732283, 2726782366991717276942138196849, 3657854499533237101379593333510, 1928578295715881845245137486456, 1263242285705730806288591202331, 3789726857117192418865773606993, 2324195368467747797703678306905, 2450093503961328663664213663678, 2827787910442071261545819733997, 3960871129884299055190637944954, 2837628186769067706678271320788]
en_e = 31087054322877663244023458448558
M = matrix(ZZ,66,66)
for i in range(64):
M[i,i] = 1
M[i,-1] = pubkey[i]
M[-2,-2] = 1
M[-2,-1] = en_e
M[-1,-1] = m
L = M.BKZ()
print(L)
想不到的是目标向量竟然在中间一行,一度以为我求错了,哭死
e_bin = [-1,-1,0,-1,-1,-1,0,-1,0,-1,-1,-1,-1,-1,-1,-1,-1,0,-1,0,-1,0,-1,0,-1,-1,-1,-1,-1,0,-1,-1,0,-1,0,0,-1,-1,-1,0,-1,0,0,0,0,0,0,-1,0,0,0,0,-1,0,0,0,0,-1,0,-1,0,0,-1,-1]
e = ''
for i in m:
if i == 1 or i == -1:
e += '1'
else:
e += '0'
e = int(e_bin,2)
# e = 15960663600754919507
高位攻击求到p,之后常规rsa
# sage
from gmpy2 import *
from Crypto.Util.number import *
p_high = 139540788452365306201344680691061363403552933527922544113532931871057569249632300961012384092481349965600565669315386312075890938848151802133991344036696488204791984307057923179655351110456639347861739783538289295071556484465877192913103980697449775104351723521120185802327587352171892429135110880845830815744
n = 22687275367292715121023165106670108853938361902298846206862771935407158965874027802803638281495587478289987884478175402963651345721058971675312390474130344896656045501040131613951749912121302307319667377206302623735461295814304029815569792081676250351680394603150988291840152045153821466137945680377288968814340125983972875343193067740301088120701811835603840224481300390881804176310419837493233326574694092344562954466888826931087463507145512465506577802975542167456635224555763956520133324723112741833090389521889638959417580386320644108693480886579608925996338215190459826993010122431767343984393826487197759618771
pbits = 1024
kbits = 435
PR.<x> = PolynomialRing(Zmod(n))
f = x + p_high
p0 = f.small_roots(X = 2 ^ kbits,beta = 0.4)[0]
# print(p_high + p0)
p = 139540788452365306201344680691061363403552933527922544113532931871057569249632300961012384092481349965600565669315386312075890938848151802133991344036696488204791984307057923179677630589032444985150800881889090713797496239571291907818169058929859395965304623825442220206712660451198754072531986630133689525911
c = 156879727064293983713540449709354153986555741467040286464656817265584766312996642691830194777204718013294370729900795379967954637233360644687807499775502507899321601376211142933572536311131955278039722631021587570212889988642265055045777870448827343999745781892044969377246509539272350727171791700388478710290244365826497917791913803035343900620641430005143841479362493138179077146820182826098057144121231954895739989984846588790277051812053349488382941698352320246217038444944941841831556417341663611407424355426767987304941762716818718024107781873815837487744195004393262412593608463400216124753724777502286239464
e = 15960663600754919507
q = n // p
d = invert(e,(p-1)*(q-1))
print(long_to_bytes(int(pow(c,d,n))))
# b'DASCTF{T81I_tPPS_6r7g_xlPi_OO3M_6vyV_Rkba}'
看完星盟安全团队的wp知道了另一种更简单的解法,通过利用超递增序列求解
en_e = (pub1 * e1) % m + ...+ (pub64 * e64) % m
又pubi = w * listi % m
=> en_e = w * (list1 * e1 + ... + list64 * e64) % m
= > e n _ e ∗ w − 1 ≡ ( l i s t 1 ∗ e 1 + . . . + l i s t 64 ∗ e 64 ) ( m o d m ) => en\_e * w ^ {-1} \equiv (list1 * e1 + ... + list64 * e64) \pmod m =>en_e∗w−1≡(list1∗e1+...+list64∗e64)(modm)
其中list是超递增序列
贴一下他们超递增解题代码:
## SageMath
import libnum, gmpy2
pubkey = [18143710780782459577, 54431132342347378731, 163293397027042136193, 489880191081126408579, 1469640573243379225737, 4408921719730137677211, 13226765159190413031633, 39680295477571239094899, 119040886432713717284697, 357122659298141151854091, 1071367977894423455562273, 3214103933683270366686819, 9642311801049811100060457, 28926935403149433300181371, 86780806209448299900544113, 260342418628344899701632339, 781027255885034699104897017, 2343081767655104097314691051, 7029245302965312291944073153, 21087735908895936875832219459, 63263207726687810627496658377, 189789623180063431882489975131, 569368869540190295647469925393, 1708106608620570886942409776179, 601827224419797931380408071500, 1805481673259393794141224214500, 893952418336266652976851386463, 2681857255008799958930554159389, 3523079163584485147344841221130, 1524252287869625983140881149316, 50264262166963219975822190911, 150792786500889659927466572733, 452378359502668979782399718199, 1357135078508006939347199154597, 4071405235524020818041597463791, 3169230503688232995231149877299, 462706308180869526799807117823, 1388118924542608580399421353469, 4164356773627825741198264060407, 3448085117999647764701149667147, 1299270151115113835209806487367, 3897810453345341505629419462101, 2648446157152195057994615872229, 3422845870014670444537026359650, 1223552407160181874717436564876, 3670657221480545624152309694628, 1966986461557807413563286569810, 1378466783231507511243038452393, 4135400349694522533729115357179, 3361215846199738142293703557463, 1038662335715384967987468158315, 3115987007146154903962404474945, 302975818554635252993570910761, 908927455663905758980712732283, 2726782366991717276942138196849, 3657854499533237101379593333510, 1928578295715881845245137486456, 1263242285705730806288591202331, 3789726857117192418865773606993, 2324195368467747797703678306905, 2450093503961328663664213663678, 2827787910442071261545819733997, 3960871129884299055190637944954, 2837628186769067706678271320788]
en_e = 31087054322877663244023458448558
w = gcd(pubkey[0], pubkey[1])
assert is_prime(w)
list1 = [pow(3, i) for i in range(64)]
m = gcd(w*list1[-1]-pubkey[-1], w*list1[-2]-pubkey[-2])
assert is_prime(m)
en_e = en_e *inverse_mod(w,m) % m
e = ''
for each in list1[::-1]:
if en_e >= each:
e += '1'
en_e -= each
else:
e += '0'
e = int(e[::-1], 2)
p0 = 139540788452365306201344680691061363403552933527922544113532931871057569249632300961012384092481349965600565669315386312075890938848151802133991344036696488204791984307057923179655351110456639347861739783538289295071556484465877192913103980697449775104351723521120185802327587352171892429135110880845830815744
n = 22687275367292715121023165106670108853938361902298846206862771935407158965874027802803638281495587478289987884478175402963651345721058971675312390474130344896656045501040131613951749912121302307319667377206302623735461295814304029815569792081676250351680394603150988291840152045153821466137945680377288968814340125983972875343193067740301088120701811835603840224481300390881804176310419837493233326574694092344562954466888826931087463507145512465506577802975542167456635224555763956520133324723112741833090389521889638959417580386320644108693480886579608925996338215190459826993010122431767343984393826487197759618771
c = 156879727064293983713540449709354153986555741467040286464656817265584766312996642691830194777204718013294370729900795379967954637233360644687807499775502507899321601376211142933572536311131955278039722631021587570212889988642265055045777870448827343999745781892044969377246509539272350727171791700388478710290244365826497917791913803035343900620641430005143841479362493138179077146820182826098057144121231954895739989984846588790277051812053349488382941698352320246217038444944941841831556417341663611407424355426767987304941762716818718024107781873815837487744195004393262412593608463400216124753724777502286239464
kbit = 435
PR.<x> = PolynomialRing(Zmod(n))
f = p0+x
x = f.small_roots(X=2^kbit, beta=0.4)
p = p0+int(x[0])
q = n // p
d = int(gmpy2.invert(e, (p-1)*(q-1)))
m = int(pow(c, d, n))
print(libnum.n2s(m)) # DASCTF{T81I_tPPS_6r7g_xlPi_OO3M_6vyV_Rkba}
SigninCrypto
题目描述:
from random import *
from Crypto.Util.number import *
from Crypto.Cipher import DES3
from flag import flag
from key import key
from iv import iv
import os
import hashlib
import secrets
K1 = key
hint1 = os.urandom(2) * 8
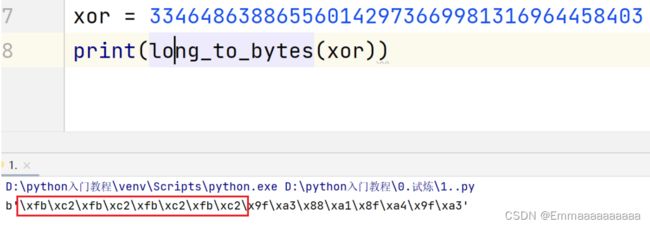
xor =bytes_to_long(hint1)^bytes_to_long(K1)
print(xor)
def Rand():
rseed = secrets.randbits(1024)
List1 = []
List2 = []
seed(rseed)
for i in range(624):
rand16 = getrandbits(16)
List1.append(rand16)
seed(rseed)
for i in range(312):
rand64 = getrandbits(64)
List2.append(rand64)
with open("task.txt", "w") as file:
for rand16 in List1:
file.write(hex(rand16)+ "\n")
for rand64 in List2:
file.write(hex((rand64 & 0xffff) | ((rand64 >> 32) & 0xffff) << 16) + "\n") # 低16位
Rand()
K2 = long_to_bytes(getrandbits(64))
K3 = flag[:8]
KEY = K1 + K2 + K3
IV=iv
IV1=IV[:len(IV)//2]
IV2=IV[len(IV)//2:]
digest1 = hashlib.sha512(IV1).digest().hex()
digest2 = hashlib.sha512(IV2).digest().hex()
digest=digest1+digest2
hint2=(bytes_to_long(IV)<<32)^bytes_to_long(os.urandom(8))
print(hex(bytes_to_long((digest.encode()))))
print(hint2)
mode = DES3.MODE_CBC
des3 = DES3.new(KEY, mode, IV)
pad_len = 8 - len(flag) % 8
padding = bytes([pad_len]) * pad_len
flag += padding
cipher = des3.encrypt(flag)
ciphertext=cipher.hex()
print(ciphertext)
xor = 334648638865560142973669981316964458403
digest_encode = 0x62343937373634656339396239663236643437363738396663393438316230353665353733303939613830616662663633326463626431643139323130616333363363326631363235313661656632636265396134336361623833636165373964343533666537663934646239396462323666316236396232303539336438336234393737363465633939623966323664343736373839666339343831623035366535373330393961383061666266363332646362643164313932313061633336336332663136323531366165663263626539613433636162383363616537396434353366653766393464623939646232366631623639623230353933643833
hint2 = 22078953819177294945130027344
ciphertext = 'a6546bd93bced0a8533a5039545a54d1fee647007df106612ba643ffae850e201e711f6e193f15d2124ab23b250bd6e1'
题目分析:
猜测hint1 = b’\xfb\xc2’ * 8
异或得到K1 = dasctfda
(K2先跳过,最后来说)
flag前7位为DASCTF{
K3 = flag[:8],即flag前8位,这意味着K3也差不多出来了,爆破一位即可
(K2,K3都是8位,那K1很大概率就是8位,所以上面求出的K1是正确的)
hint2长度95,95-32 = 63,可以知道IV是64位(前导0省略了)
可以求出IV的前4个字节(32bits)为GWHT,由此得到IV1 = GWHT
知道了digest_encode,又知道了IV1,那么IV2也可以求出来
digest1 = hashlib.sha512(IV1).digest().hex()
digest2 = hashlib.sha512(IV2).digest().hex()
digest=digest1+digest2
hint2=(bytes_to_long(IV)<<32)^bytes_to_long(os.urandom(8))
IV1 = b'GWHT'
digest1 = hashlib.sha512(IV1).digest().hex()
digest11 = bytes_to_long(digest1.encode())
digest2 = long_to_bytes((digest_encode - (digest11 << (8 * 128))))
print(digest2)可以发现digest2 = digest1,由此可知IV2 = IV1 = GWHT
由此未知量都出来了,只剩K2了
随机数生成机制:都是通过生成32bits的数
生成16bits:先生成32bits,再取此数高16位
生成64bits:先生成两个32bits的数X1,X2,再拼接X2||X1
知道了生成机制,那么K2也就能出来了
for i in range(624):
rand16 = getrandbits(16)
从这里我们知道了624个32bits数的高16位
file.write(hex((rand64 & 0xffff) | ((rand64 >> 32) & 0xffff) << 16) + "\n")
从这里我们知道了624个32bits数的低16位
拼接一下即可得到624个32bits数,之后便是普普通通的随机数预测了
至此所有未知量都出来了,flag也就出来了
完整代码如下:
from Crypto.Util.number import *
from randcrack import RandCrack
from Crypto.Cipher import DES3
with open('task.txt','r') as f:
f = f.readlines()
data = [eval(i) for i in f]
ran16 = data[:624]
ran64 = data[-312:]
ran64_ = []
for i in ran64:
ran64_.append(i & 0xffff)
ran64_.append(i >> 16)
ran32 = []
for i in range(624):
ran32.append((ran16[i] << 16) + ran64_[i])
rc = RandCrack()
for i in ran32:
rc.submit(i)
K2 = long_to_bytes(rc.predict_getrandbits(64))
K1 = b'dasctfda'
IV1 = b'GWHT'
IV2 = b'GWHT'
IV = IV1 + IV2
ciphertext = 'a6546bd93bced0a8533a5039545a54d1fee647007df106612ba643ffae850e201e711f6e193f15d2124ab23b250bd6e1'
c = bytes.fromhex(ciphertext)
mode = DES3.MODE_CBC
for i in range(256):
K3 = b'DASCTF{' + bytes([i])
KEY = K1 + K2 + K3
des3 = DES3.new(KEY, mode, IV)
m = des3.decrypt(c)
if b'CTF' in m:
print(m)
# DASCTF{8e5ee461-f4e1-4af2-8632-c9d62f4dc073}
esyRSA
题目描述:
from gmpy2 import invert
from md5 import md5
from secret import p, q
e = ?????
n = p*q
phi = (p-1)*(q-1)
d = invert(e, phi)
ans = gcd(e,phi)
print n, e, d
print "Flag: DASCTF{%s}" %md5(str(p + q)).hexdigest()
"""
n = 8064259277274639864655809758868795854117113170423331934498023294296505063511386001711751916634810056911517464467899780578338013011453082479880809823762824723657495915284790349150975180933698827382368698861967973964030509129133021116919437755292590841218316278732797712538885232908975173746394816520256585937380642592772746398646558097588687958541171131704233319344980232942965050635113860017117519166348100569115174644678997805783380130114530824798808098237628247236574959152847903491509751809336988273823686988619679739640305091291330211169194377552925908412183162787327977125388852329089751737463948165202565859373
d = 14218766449983537783699024084862960813708451888387858392014856544340557703876299258990323621963898510226357248200187173211121827541826897886277531706124228848229095880229718049075745233893843373402201077890407507625110061976931591596708901741146750809962128820611844426759462132623616118530705745098783140913
"""
题目分析:
这题真的,没发现n重复了 这正常人哪想得到所给的n会出问题
步入正题
e ∗ d = 1 m o d p h i ⇒ e ∗ d = 1 + k ∗ p h i ⇒ d p h i − k e = 1 e ∗ p h i p h i ≈ n , 且 p h i 非常大 ⇒ d n − k e = 1 e ∗ p h i 也就是说 d / n 与 k / d 非常接近,而 d / n 又已知 对 d / n 进行连分数展开,得到一串分数的分母很可能是 e 至此得到 k , e ⇒ p + q = n + 1 − ( e ∗ d − 1 ) / / k e * d = 1 \mod phi\\ \Rightarrow e * d = 1 + k * phi\\ \Rightarrow \frac{d}{phi} - \frac{k}{e} = \frac{1}{e * phi}\\ phi\approx n,且phi非常大\\ \Rightarrow \frac{d}{n} - \frac{k}{e} = \frac{1}{e * phi}\\ 也就是说d /n与k/d非常接近,而d/n又已知\\ 对d/n进行连分数展开,得到一串分数的分母很可能是e\\至此得到k,e\\ \Rightarrow p + q = n + 1 - (e * d - 1) // k e∗d=1modphi⇒e∗d=1+k∗phi⇒phid−ek=e∗phi1phi≈n,且phi非常大⇒nd−ek=e∗phi1也就是说d/n与k/d非常接近,而d/n又已知对d/n进行连分数展开,得到一串分数的分母很可能是e至此得到k,e⇒p+q=n+1−(e∗d−1)//k
from Crypto.Util.number import *
from gmpy2 import *
n = 80642592772746398646558097588687958541171131704233319344980232942965050635113860017117519166348100569115174644678997805783380130114530824798808098237628247236574959152847903491509751809336988273823686988619679739640305091291330211169194377552925908412183162787327977125388852329089751737463948165202565859373
d = 14218766449983537783699024084862960813708451888387858392014856544340557703876299258990323621963898510226357248200187173211121827541826897886277531706124228848229095880229718049075745233893843373402201077890407507625110061976931591596708901741146750809962128820611844426759462132623616118530705745098783140913
c = continued_fraction(d/n)
for i in range(1, 500):
k = int(c.numerator(i)) # 分子
e = int(c.denominator(i))
if (e * d - 1) % k==0:
print(k)
print(e)
p_q = n + 1 - (e * d - 1) // k
print('p + q =', p_q)
2384
13521
p + q = 18101966903197904104103274369549488558638013636328319260314053428770825687572755141919313812981523970938045930012152983362607947170555142776865084844865966
注意这一串,e为5位数,正好符合题目要求
# import hashlib
a = 18101966903197904104103274369549488558638013636328319260314053428770825687572755141919313812981523970938045930012152983362607947170555142776865084844865966
print(hashlib.md5(str(a).encode()).hexdigest())
# DASCTF{4ae33bea90f030bfddb7ac4d9222ef8f}
拓展:
连分数嘛,用维纳攻击代码也行,维纳攻击代码核心就在连分数这里,只要修改一下条件即可:
from gmpy2 import *
from Crypto.Util.number import *
import random
def continuedFra(x, y):
cf = []
while y:
cf.append(x // y)
x, y = y, x % y
return cf
def gradualFra(cf):
numerator = 0 # 分子
denominator = 1 # 分母
for x in cf[::-1]:
# 这里的渐进分数分子分母要分开
numerator, denominator = denominator, x * denominator + numerator
return numerator, denominator
def getGradualFra(cf):
gf = []
for i in range(1, len(cf) + 1):
gf.append(gradualFra(cf[:i]))
return gf
def wienerAttack(d, n):
cf = continuedFra(d, n)
gf = getGradualFra(cf)
for e,k in gf: # 不得不说最后要倒一下呀!
if e == 1:
continue
if (e * d - 1) % k == 0:
print(k)
print(e)
p_q = n + 1 - (e * d - 1) // k
print('p + q =', p_q)
n = 80642592772746398646558097588687958541171131704233319344980232942965050635113860017117519166348100569115174644678997805783380130114530824798808098237628247236574959152847903491509751809336988273823686988619679739640305091291330211169194377552925908412183162787327977125388852329089751737463948165202565859373
d = 14218766449983537783699024084862960813708451888387858392014856544340557703876299258990323621963898510226357248200187173211121827541826897886277531706124228848229095880229718049075745233893843373402201077890407507625110061976931591596708901741146750809962128820611844426759462132623616118530705745098783140913
a = wienerAttack(d,n)
所以说涉及连分数都可用维纳攻击代码,只需把条件稍微修改下,不过sage里面的continued_fraction()函数确实是更简洁
浅记一下
以上题目分析挺详细的吧哈哈
关键词:有限域开方(或AMM),格,私钥文件损坏,16位随机数预测机制,连分数,超递增
本次比赛只做出了前四道,题目难度中等,适合我这种小菜做。
SigninCrypto中的16位随机数预测机制我是真不知道,当时就困在K2,好难受,还是学的不扎实。esyRSA中的n重复了我也没发现,当时确实疑惑了,因为n分解出来好多数,会导致p或q不为素数,但之后也没多想了,唉。
现在细细想想,确实有问题,e * d = 1 % phi,不管e多大,d的数量级都会和phi差不多(也会和n差不多),然而此题中,相差巨大,两倍了,不合理,所以n有问题,事实也确实如此。唉,就这样吧,一起加油吧。