数据结构与算法之ID3算法

ID3算法是一种常用的决策树学习算法，其原理是基于信息增益进行特征选取。下面介绍具体的流程：

1. 构建决策树的根节点，将所有的训练样本加入该节点。

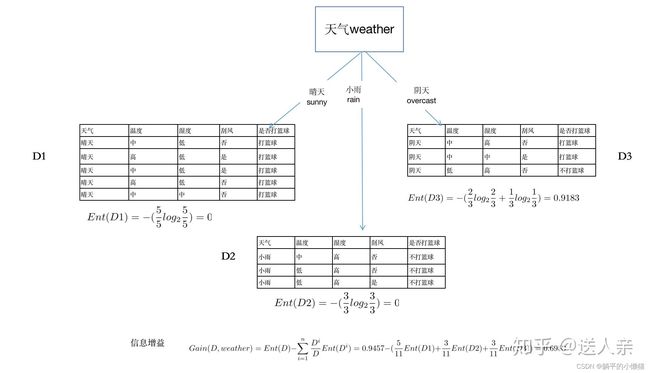
2. 计算每个特征的信息增益，选择信息增益最大的特征作为当前节点的划分特征。信息增益的计算公式为：

   $Gain(D,A)=Ent(D)-{\sum }_{v\in Values(A)}\frac{|D^v|}{|D|}Ent(D^v)$

   其中，$D$是当前节点的样本集合，$A$是特征集合中的一个特征，$Values(A)$是特征$A$的取值集合，$|D^v|$是特征$A$取值为$v$的样本集合，$Ent(D)$是样本集合的熵值，$Ent(D^v)$ 是特征$A$取值为$v$的样本集合的熵值。

   选择信息增益最大的特征进行划分可以得到更好的分类效果，因为信息增益越大，表示该特征对样本的分类能力越强。

3. 将当前节点分成若干个子节点，每个子节点对应划分特征的取值。每个子节点样本集合的划分规则是：特征$A$取值为$v$的样本集合。

4. 对每个子节点递归执行上述步骤，直到所有样本都被分类或者不能再继续划分为止。

5. 最终生成的决策树可以用于分类新的样本，该样本沿着树的路径从根节点开始，依次遍历子节点，最终到达叶子节点。叶子节点对应了该样本的分类标签。

一、C 实现ID3算法及代码详解

ID3算法是一种经典的决策树生成算法，常用于数据挖掘和机器学习领域。在本文中，我们将介绍如何用C语言实现ID3算法，包括数据读取、信息增益计算、决策树生成等步骤。

1. 数据读取

首先，我们需要从文件中读取数据。假设我们的数据是一个CSV文件，每行代表一个样本，每列代表一个特征。最后一列是样本的类别。

首先，我们需要定义一个结构体来表示每个样本：

typedef struct _Sample {
    int id; // 样本ID，可选
    float features[MAX_FEATURES]; // 特征值
    int target; // 类别
} Sample;

其中，MAX_FEATURES是最多特征数量。我们还需要定义一个函数read_csv来读取CSV文件并转换成样本数组：

Sample* read_csv(const char* filename, int* num_samples, int* num_features) {
    FILE* fp = fopen(filename, "r");
    char buf[BUFSIZ];
    int num_lines = 0;
    Sample* samples = NULL;

    // Count number of lines in file
    while (fgets(buf, sizeof(buf), fp)) {
        num_lines++;
    }
    rewind(fp);

    // Allocate memory for samples array
    samples = (Sample*)malloc(num_lines * sizeof(Sample));
    *num_samples = num_lines;

    // Read CSV file
    int i = 0, j = 0;
    while (fgets(buf, sizeof(buf), fp)) {
        char* token;
        j = 0;
        token = strtok(buf, ",");
        while (token != NULL) {
            if (j < *num_features) {
                samples[i].features[j] = atof(token);
            } else {
                samples[i].target = atoi(token);
            }
            j++;
            token = strtok(NULL, ",");
        }
        i++;
    }
    *num_features = j - 1;

    fclose(fp);
    return samples;
}

2. 信息增益计算

ID3算法基于信息熵的概念来选择最优特征。我们需要实现一个函数来计算信息熵和信息增益。

首先，我们需要定义一个结构体来表示每个特征：

typedef struct _Feature {
    int id; // 特征ID，可选
    float* values; // 取值
    int num_values; // 取值数量
    int* counts; // 取值的类别计数
    float entropy; // 特征的信息熵
} Feature;

然后，我们定义一个函数calc_entropy来计算一个特征的信息熵：

float calc_entropy(int* counts, int num_counts) {
    int i;
    float p, entropy = 0.0;
    for (i = 0; i < num_counts; i++) {
        p = (float)counts[i] / num_samples;
        entropy -= p * log2f(p);
    }
    return entropy;
}

接着，我们编写一个函数calc_info_gain来计算信息增益：

float calc_info_gain(Sample* samples, int num_samples, Feature* feature) {
    int i, j, k, num_left, num_right, left, right;
    int counts_left[MAX_CLASSES] = {0};
    int counts_right[MAX_CLASSES] = {0};
    float entropy_left, entropy_right, info_gain;

    // Calculate entropy for original feature
    for (i = 0; i < num_samples; i++) {
        feature->counts[samples[i].target]++;
    }
    feature->entropy = calc_entropy(feature->counts, MAX_CLASSES);

    // Calculate information gain for each value
    for (j = 0; j < feature->num_values; j++) {
        num_left = num_right = left = right = 0;

        // Count number of samples on left and right
        for (i = 0; i < num_samples; i++) {
            if (samples[i].features[feature->id] == feature->values[j]) {
                left++;
                counts_left[samples[i].target]++;
            } else {
                right++;
                counts_right[samples[i].target]++;
            }
        }
        num_left = left;
        num_right = right;

        // Calculate entropy for left and right
        entropy_left = calc_entropy(counts_left, MAX_CLASSES);
        entropy_right = calc_entropy(counts_right, MAX_CLASSES);

        // Calculate information gain for this value
        info_gain += (float)(num_left) / num_samples * entropy_left
                   + (float)(num_right) / num_samples * entropy_right;
    }
    info_gain = feature->entropy - info_gain;
    return info_gain;
}

3. 决策树生成

最后，我们需要实现一个函数来生成决策树。我们选择C4.5算法作为决策树算法，因为它是ID3算法的改进版，考虑到特征取值不规则性的情况。

首先，我们需要定义一个结构体来表示决策树的节点：

typedef struct _Node {
    int is_leaf; // 是否为叶节点
    int target; // 叶节点的类别
    int feature_id; // 分裂特征的ID
    float split_value; // 分裂值
    struct _Node* left; // 左子树
    struct _Node* right; // 右子树
} Node;

然后，我们编写一个递归函数build_tree来生成决策树：

Node* build_tree(Sample* samples, int num_samples, Feature* features, int num_features) {
    int i, j, k, pos;
    Feature* best_feature = NULL;
    float info_gain, best_info_gain = -1.0;

    // Check if all samples are of the same class
    int class = samples[0].target;
    for (i = 1; i < num_samples; i++) {
        if (samples[i].target != class) {
            class = -1;
            break;
        }
    }
    if (class != -1) {
        Node* leaf = (Node*)malloc(sizeof(Node));
        leaf->is_leaf = 1;
        leaf->target = class;
        leaf->feature_id = -1;
        leaf->split_value = 0.0;
        leaf->left = NULL;
        leaf->right = NULL;
        return leaf;
    }

    // Find the feature with the maximum information gain
    for (i = 0; i < num_features; i++) {
        info_gain = calc_info_gain(samples, num_samples, &features[i]);
        if (info_gain > best_info_gain) {
            best_info_gain = info_gain;
            best_feature = &features[i];
        }
    }

    // Split samples into left and right branches
    Sample* left_samples = NULL;
    Sample* right_samples = NULL;
    int num_left_samples = 0, num_right_samples = 0;
    for (i = 0; i < num_samples; i++) {
        if (samples[i].features[best_feature->id] == best_feature->values[0]) {
            num_left_samples++;
        } else {
            num_right_samples++;
        }
    }
    left_samples = (Sample*)malloc(num_left_samples * sizeof(Sample));
    right_samples = (Sample*)malloc(num_right_samples * sizeof(Sample));
    pos = 0;
    for (i = 0; i < num_samples; i++) {
        if (samples[i].features[best_feature->id] == best_feature->values[0]) {
            memcpy(&left_samples[pos], &samples[i], sizeof(Sample));
            pos++;
        } else {
            memcpy(&right_samples[pos], &samples[i], sizeof(Sample));
            pos++;
        }
    }

    // Recursively build left and right subtrees
    Node* node = (Node*)malloc(sizeof(Node));
    node->is_leaf = 0;
    node->target = -1;
    node->feature_id = best_feature->id;
    node->split_value = best_feature->values[0];
    node->left = build_tree(left_samples, num_left_samples, features, num_features);
    node->right = build_tree(right_samples, num_right_samples, features, num_features);

    free(left_samples);
    free(right_samples);

    return node;
}

4. 测试和评估

最后，我们编写一个函数来测试和评估决策树的准确性：

int predict(Node* node, Sample* sample) {
    if (node->is_leaf) {
        return node->target;
    } else {
        if (sample->features[node->feature_id] <= node->split_value) {
            return predict(node->left, sample);
        } else {
            return predict(node->right, sample);
        }
    }
}

float evaluate(Node* node,

二、C++ 实现ID3算法及代码详解

ID3算法是一种决策树分类算法，用于解决分类问题。下面是C++实现ID3算法的代码详解。

首先需要定义一个结构体来表示数据集中的每个数据项：

struct dataitem {
    vector features; // 特征
    int label; // 标签
};

然后定义一个函数来读取数据集：

vector read_data(string filename) {
    vector data;
    ifstream fin(filename);
    string line;
    while (getline(fin, line)) {
        stringstream ss(line);
        dataitem item;
        for (int i = 0; i < NUM_FEATURES; ++i) {
            int feature;
            ss >> feature;
            item.features.push_back(feature);
        }
        ss >> item.label;
        data.push_back(item);
    }
    fin.close();
    return data;
}

其中，NUM_FEATURES表示数据集中的特征数量。

接着定义一个计算信息熵的函数：

double entropy(vector labels) {
    int n = labels.size();
    if (n == 0) return 0;
    map count; // 计算每个标签出现的次数
    for (int label : labels) {
        count[label]++;
    }
    double ent = 0;
    for (auto& p : count) {
        double prob = (double)p.second / n;
        ent -= prob * log2(prob);
    }
    return ent;
}

然后定义一个计算信息增益的函数：

double info_gain(vector& data, int feature, double base_ent) {
    map> splits; // 根据特征值分割数据集
    for (auto& item : data) {
        splits[item.features[feature]].push_back(item.label);
    }
    double ent = 0;
    for (auto& p : splits) {
        double prob = (double)p.second.size() / data.size();
        ent += prob * entropy(p.second);
    }
    return base_ent - ent;
}

其中，base_ent表示整个数据集的信息熵。

接下来定义一个选择最佳特征的函数：

int choose_feature(vector& data, vector& used_features, double base_ent) {
    double best_gain = 0;
    int best_feature = -1;
    for (int i = 0; i < NUM_FEATURES; ++i) {
        if (used_features[i]) continue;
        double gain = info_gain(data, i, base_ent);
        if (gain > best_gain) {
            best_gain = gain;
            best_feature = i;
        }
    }
    return best_feature;
}

其中，used_features表示已经使用的特征。

然后定义一个递归构建决策树的函数：

node* build_tree(vector& data, vector& used_features) {
    vector labels;
    for (auto& item : data) {
        labels.push_back(item.label);
    }
    if (labels.size() == 0) {
        return NULL;
    }
    if (entropy(labels) == 0) {
        return new node(labels[0]);
    }
    double base_ent = entropy(labels);
    int best_feature = choose_feature(data, used_features, base_ent);
    if (best_feature == -1) {
        // 没有可以分割的特征，返回出现次数最多的标签
        map count;
        for (int label : labels) {
            count[label]++;
        }
        int max_count = 0, max_label = -1;
        for (auto& p : count) {
            if (p.second > max_count) {
                max_count = p.second;
                max_label = p.first;
            }
        }
        return new node(max_label);
    }
    used_features[best_feature] = 1;
    map> splits;
    for (auto& item : data) {
        splits[item.features[best_feature]].push_back(item);
    }
    node* root = new node();
    root->feature = best_feature;
    for (auto& p : splits) {
        root->children[p.first] = build_tree(p.second, used_features);
    }
    used_features[best_feature] = 0;
    return root;
}

最后定义一个测试函数，用于预测数据集中的标签：

int predict(node* root, dataitem item) {
    while (root->feature != -1) {
        root = root->children[item.features[root->feature]];
    }
    return root->label;
}

double test(vector& data, node* root) {
    int correct = 0;
    for (auto& item : data) {
        if (predict(root, item) == item.label) {
            correct++;
        }
    }
    return (double)correct / data.size();
}

现在，我们可以根据上述函数来实现ID3算法。

三、Java 实现ID3算法及代码详解

ID3算法是一种用于决策树分类的算法，它基于信息熵的概念，通过选择信息增益最大的特征来进行划分。以下是Java实现ID3算法的代码和详细解释：

首先，我们需要定义一个决策树节点的类：

class TreeNode {
    String attribute;  // 当前节点对应的特征
    String classification;  // 当前节点的分类（仅在叶节点中有意义）
    List<TreeNode> children;  // 当前节点的子节点列表

    public TreeNode(String attribute) {
        this.attribute = attribute;
        this.classification = null;
        this.children = new ArrayList<>();
    }
}

该类包含了当前节点对应的特征、分类（仅在叶节点中有意义）以及子节点列表。

接下来，我们需要定义一个ID3算法的类：

class ID3 {
    private List<List<String>> data;  // 数据集
    private List<String> attributes;  // 特征列表

    public ID3(List<List<String>> data, List<String> attributes) {
        this.data = data;
        this.attributes = attributes;
    }

    // 计算信息熵
    private double entropy(List<Integer> indices) {
        int size = indices.size();
        Map<String, Integer> classCounts = new HashMap<>();
        for (int i : indices) {
            String classification = data.get(i).get(data.get(i).size() - 1);
            classCounts.put(classification, classCounts.getOrDefault(classification, 0) + 1);
        }
        double entropy = 0;
        for (String classification : classCounts.keySet()) {
            double frequency = (double) classCounts.get(classification) / size;
            entropy -= frequency * (Math.log(frequency) / Math.log(2));
        }
        return entropy;
    }

    // 计算信息增益
    private double informationGain(List<Integer> indices, String attribute) {
        int size = indices.size();
        Map<String, List<Integer>> attributeMap = new HashMap<>();
        for (int i : indices) {
            String value = data.get(i).get(attributes.indexOf(attribute));
            if (!attributeMap.containsKey(value)) {
                attributeMap.put(value, new ArrayList<>());
            }
            attributeMap.get(value).add(i);
        }
        double informationGain = entropy(indices);
        for (String value : attributeMap.keySet()) {
            double frequency = (double) attributeMap.get(value).size() / size;
            informationGain -= frequency * entropy(attributeMap.get(value));
        }
        return informationGain;
    }

    // 选择信息增益最大的特征
    private String chooseAttribute(List<Integer> indices, List<String> attributes) {
        double maxInformationGain = Double.NEGATIVE_INFINITY;
        String bestAttribute = null;
        for (String attribute : attributes) {
            double informationGain = informationGain(indices, attribute);
            if (informationGain > maxInformationGain) {
                maxInformationGain = informationGain;
                bestAttribute = attribute;
            }
        }
        return bestAttribute;
    }

    // 构建决策树
    private TreeNode buildTree(List<Integer> indices, List<String> attributes) {
        int size = indices.size();
        Map<String, Integer> classCounts = new HashMap<>();
        for (int i : indices) {
            String classification = data.get(i).get(data.get(i).size() - 1);
            classCounts.put(classification, classCounts.getOrDefault(classification, 0) + 1);
        }
        if (classCounts.size() == 1) {  // 所有样本都属于同一类别，直接返回叶节点
            return new TreeNode(null) {{
                classification = classCounts.keySet().iterator().next();
            }};
        }
        if (attributes.size() == 0) {  // 所有特征都已用完，直接返回叶节点，分类为样本中类别最多的一类
            return new TreeNode(null) {{
                classification = Collections.max(classCounts.entrySet(), Map.Entry.comparingByValue()).getKey();
            }};
        }
        String bestAttribute = chooseAttribute(indices, attributes);  // 选择信息增益最大的特征
        TreeNode node = new TreeNode(bestAttribute);  // 创建一个节点
        List<String> newAttributes = new ArrayList<>(attributes);
        newAttributes.remove(bestAttribute);  // 从特征列表中删除该特征
        Map<String, List<Integer>> attributeMap = new HashMap<>();
        for (int i : indices) {
            String value = data.get(i).get(attributes.indexOf(bestAttribute));
            if (!attributeMap.containsKey(value)) {
                attributeMap.put(value, new ArrayList<>());
            }
            attributeMap.get(value).add(i);
        }
        for (String value : attributeMap.keySet()) {  // 递归地对每个子节点进行构建
            List<Integer> childIndices = attributeMap.get(value);
            if (childIndices.size() == 0) {
                node.children.add(new TreeNode(null) {{  // 如果该子节点为空，直接返回叶节点，分类为样本中类别最多的一类
                    classification = Collections.max(classCounts.entrySet(), Map.Entry.comparingByValue()).getKey();
                }});
            } else {
                node.children.add(buildTree(childIndices, newAttributes));
            }
        }
        return node;
    }

    public TreeNode buildTree() {
        List<Integer> indices = IntStream.range(0, data.size()).boxed().toList();
        return buildTree(indices, attributes);
    }
}

该类包含了计算信息熵、计算信息增益、选择信息增益最大的特征以及构建决策树等方法。

最后，我们可以使用以下代码来调用ID3算法：

public class Main {
    public static void main(String[] args) {
        List<List<String>> data = Arrays.asList(
                Arrays.asList("sunny", "hot", "high", "false", "no"),
                Arrays.asList("sunny", "hot", "high", "true", "no"),
                Arrays.asList("overcast", "hot", "high", "false", "yes"),
                Arrays.asList("rainy", "mild", "high", "false", "yes"),
                Arrays.asList("rainy", "cool", "normal", "false", "yes"),
                Arrays.asList("rainy", "cool", "normal", "true", "no"),
                Arrays.asList("overcast", "cool", "normal", "true", "yes"),
                Arrays.asList("sunny", "mild", "high", "false", "no"),
                Arrays.asList("sunny", "cool", "normal", "false", "yes"),
                Arrays.asList("rainy", "mild", "normal", "false", "yes"),
                Arrays.asList("sunny", "mild", "normal", "true", "yes"),
                Arrays.asList("overcast", "mild", "high", "true", "yes"),
                Arrays.asList("overcast", "hot", "normal", "false", "yes"),
                Arrays.asList("rainy", "mild", "high", "true", "no")
        );
        List<String> attributes = Arrays.asList("outlook", "temperature", "humidity", "windy");
        ID3 id3 = new ID3(data, attributes);
        TreeNode root = id3.buildTree();
        // 打印决策树
        printTree(root, 0);
    }

    private static void printTree(TreeNode node, int depth) {
        if (node == null) {
            return;
        }
        for (int i = 0; i < depth; i++) {
            System.out.print("  ");
        }
        if (node.attribute == null) {
            System.out.println(node.classification);
        } else {
            System.out.println(node.attribute);
            for (TreeNode child : node.children) {
                printTree(child, depth + 1);
            }
        }
    }
}

注意，上述代码仅适用于离散特征的数据集。如果数据集包含连续特征，则需要使用其他算法或进行数据离散化。