《动手学深度学习 Pytorch版》 10.6 自注意力和位置编码
在注意力机制中,每个查询都会关注所有的键-值对并生成一个注意力输出。由于查询、键和值来自同一组输入,因此被称为 自注意力(self-attention),也被称为内部注意力(intra-attention)。本节将使用自注意力进行序列编码,以及使用序列的顺序作为补充信息。
import math
import torch
from torch import nn
from d2l import torch as d2l
10.6.1 自注意力
给定一个由词元组成的输入序列 x 1 , … , x n \boldsymbol{x}_1,\dots,\boldsymbol{x}_n x1,…,xn,其中任意 x i ∈ R d ( 1 ≤ i ≤ n ) \boldsymbol{x}_i\in\R^d\quad(1\le i\le n) xi∈Rd(1≤i≤n) 。该序列的自注意力输出为一个长度相同的序列 y 1 , … , y n \boldsymbol{y}_1,\dots,\boldsymbol{y}_n y1,…,yn,其中:
y i = f ( x i , ( x 1 , x 1 ) , … , ( x n , x n ) ) ∈ R d \boldsymbol{y}_i=f(\boldsymbol{x}_i,(\boldsymbol{x}_1,\boldsymbol{x}_1),\dots,(\boldsymbol{x}_n,\boldsymbol{x}_n))\in\R^d yi=f(xi,(x1,x1),…,(xn,xn))∈Rd
num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens, # 基于多头注意力对一个张量完成自注意力的计算
num_hiddens, num_heads, 0.5)
attention.eval()
MultiHeadAttention(
(attention): DotProductAttention(
(dropout): Dropout(p=0.5, inplace=False)
)
(W_q): Linear(in_features=100, out_features=100, bias=False)
(W_k): Linear(in_features=100, out_features=100, bias=False)
(W_v): Linear(in_features=100, out_features=100, bias=False)
(W_o): Linear(in_features=100, out_features=100, bias=False)
)
batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens)) # 张量的形状为(批量大小,时间步的数目或词元序列的长度,d)。
attention(X, X, X, valid_lens).shape # 输出与输入的张量形状相同
torch.Size([2, 4, 100])
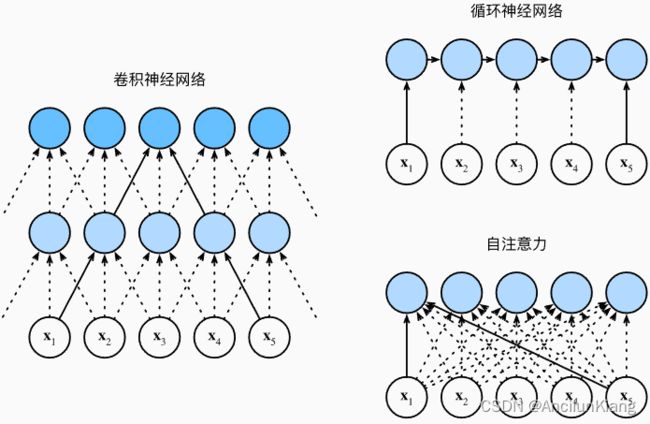
10.6.2 比较卷积神经网络、循环神经网络和自注意力
-
卷积神经网络
-
计算复杂度为 O ( k n d 2 ) O(knd^2) O(knd2)
-
k k k 为卷积核大小
-
n n n 为序列长度是
-
d d d 为输入和输出的通道数量
-
-
并行度为 O ( n ) O(n) O(n)
-
最大路径长度为 O ( n / k ) O(n/k) O(n/k)
-
-
循环神经网络
-
计算复杂度为 O ( n d 2 ) O(nd^2) O(nd2)
d × d d\times d d×d 权重矩阵和 d d d 维隐状态的乘法计算复杂度为 O ( d 2 ) O(d^2) O(d2),由于序列长度为 n n n,因此循环神经网络层的计算复杂度为 O ( n d 2 ) O(nd^2) O(nd2)
-
并行度为 O ( 1 ) O(1) O(1)
有 O ( n ) O(n) O(n) 个顺序操作无法并行化。
-
最大路径长度也是 O ( n ) O(n) O(n)
-
-
自注意力
-
计算复杂度为 O ( n 2 d ) O(n^2d) O(n2d)
查询、键和值都是 n × d n\times d n×d 矩阵
-
并行度为 O ( n ) O(n) O(n)
每个词元都通过自注意力直接连接到任何其他词元。因此有 O ( 1 ) O(1) O(1) 个顺序操作可以并行计算
-
最大路径长度也是 O ( 1 ) O(1) O(1)
-
总而言之,卷积神经网络和自注意力都拥有并行计算的优势,而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方,所以在很长的序列中计算会非常慢。
10.6.3 位置编码
在处理词元序列时,循环神经网络是逐个的重复地处理词元的,而自注意力则因为并行计算而放弃了顺序操作。为了使用序列的顺序信息,通过在输入表示中添加 位置编码(positional encoding) 来注入绝对的或相对的位置信息。位置编码可以通过学习得到也可以直接固定得到。
基于正弦函数和余弦函数的固定位置编码的矩阵第 i i i 行、第 2 j 2j 2j 列和 2 j + 1 2j+1 2j+1 列上的元素为:
p i , 2 j = sin ( i 1000 0 2 j / d ) p i , 2 j + 1 = cos ( i 1000 0 2 j / d ) \begin{align} p_{i,2j}&=\sin{\left(\frac{i}{10000^{2j/d}}\right)}\\ p_{i,2j+1}&=\cos{\left(\frac{i}{10000^{2j/d}}\right)} \end{align} pi,2jpi,2j+1=sin(100002j/di)=cos(100002j/di)
#@save
class PositionalEncoding(nn.Module):
"""位置编码"""
def __init__(self, num_hiddens, dropout, max_len=1000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(dropout)
# 创建一个足够长的P
self.P = torch.zeros((1, max_len, num_hiddens))
X = torch.arange(max_len, dtype=torch.float32).reshape(
-1, 1) / torch.pow(10000, torch.arange(
0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
self.P[:, :, 0::2] = torch.sin(X)
self.P[:, :, 1::2] = torch.cos(X)
def forward(self, X):
X = X + self.P[:, :X.shape[1], :].to(X.device)
return self.dropout(X)
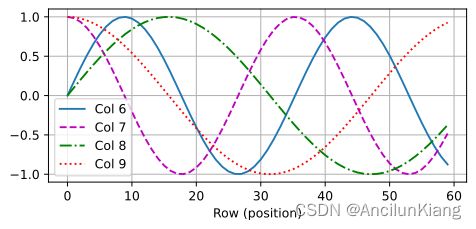
在位置嵌入矩阵 P \boldsymbol{P} P 中,行代表词元在序列中的位置,列代表位置编码的不同维度。从下面的例子中可以看到位置嵌入矩阵的第 6 列和第 7 列的频率高于第 8 列和第 9 列。第 6 列和第 7 列之间的偏移量(第 8 列和第 9 列相同)是由于正弦函数和余弦函数的交替。
encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])
10.6.3.1 绝对位置信息
打印出 0 , 1 , … , 7 0,1,\dots,7 0,1,…,7 的二进制表示形式即可明白沿着编码维度单调降低的频率与绝对位置信息的关系。
每个数字、每两个数字和每四个数字上的比特值在第一个最低位、第二个最低位和第三个最低位上分别交替。
for i in range(8):
print(f'{i}的二进制是:{i:>03b}')
0的二进制是:000
1的二进制是:001
2的二进制是:010
3的二进制是:011
4的二进制是:100
5的二进制是:101
6的二进制是:110
7的二进制是:111
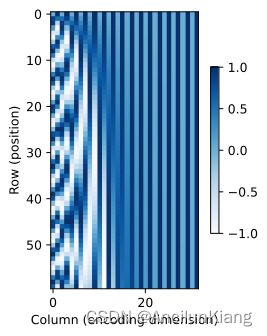
在二进制表示中,较高比特位的交替频率低于较低比特位,与下面的热图所示相似,只是位置编码通过使用三角函数在编码维度上降低频率。由于输出是浮点数,因此此类连续表示比二进制表示法更节省空间。
P = P[0, :, :].unsqueeze(0).unsqueeze(0)
d2l.show_heatmaps(P, xlabel='Column (encoding dimension)',
ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')
10.6.3.2 相对位置信息
除了捕获绝对位置信息之外,上述的位置编码还允许模型学习得到输入序列中相对位置信息。这是因为对于任何确定的位置偏移 δ \delta δ,位置 i + δ i+\delta i+δ 处的位置编码可以线性投影位置 i i i 处的位置编码来表示。
这种投影的数学解释是,令 ω j = 1 / 1000 0 2 j / d \omega_j=1/10000^{2j/d} ωj=1/100002j/d,对于任何确定的位置偏移 δ \delta δ,上个式子中的任何一对 ( p i , 2 j , p i , 2 j + 1 ) (p_{i,2j},p_{i,2j+1}) (pi,2j,pi,2j+1) 都可以线性投影到 ( p i + δ , 2 j , p i + δ , 2 j + 1 ) (p_{i+\delta,2j},p_{i+\delta,2j+1}) (pi+δ,2j,pi+δ,2j+1):
[ cos ( δ ω j ) sin ( δ ω j ) − sin ( δ ω j ) cos ( δ ω j ) ] [ p i , 2 j p i , 2 j + 1 ] = [ cos ( δ ω j ) sin ( i ω j ) + sin ( δ ω j ) cos ( i ω j ) − sin ( δ ω j ) sin ( i ω j ) + cos ( δ ω j ) cos ( i ω j ) ] = [ sin ( ( i + δ ) ω j ) cos ( ( i + δ ) ω j ) ] = [ p i , 2 j p i , 2 j + 1 ] \begin{align} &\begin{bmatrix} \cos{(\delta\omega_j)} & \sin{(\delta\omega_j)}\\ -\sin{(\delta\omega_j)} & \cos{(\delta\omega_j)} \end{bmatrix} \begin{bmatrix} p_{i,2j}\\ p_{i,2j+1} \end{bmatrix}\\ =&\begin{bmatrix} \cos{(\delta\omega_j)}\sin{(i\omega_j)}+\sin{(\delta\omega_j)}\cos{(i\omega_j)}\\ -\sin{(\delta\omega_j)}\sin{(i\omega_j)}+\cos{(\delta\omega_j)}\cos{(i\omega_j)} \end{bmatrix}\\ =&\begin{bmatrix} \sin{((i+\delta)\omega_j)}\\ \cos{((i+\delta)\omega_j)} \end{bmatrix}\\ =&\begin{bmatrix} p_{i,2j}\\ p_{i,2j+1} \end{bmatrix} \end{align} ===[cos(δωj)−sin(δωj)sin(δωj)cos(δωj)][pi,2jpi,2j+1][cos(δωj)sin(iωj)+sin(δωj)cos(iωj)−sin(δωj)sin(iωj)+cos(δωj)cos(iωj)][sin((i+δ)ωj)cos((i+δ)ωj)][pi,2jpi,2j+1]
2 × 2 2\times 2 2×2 投影矩阵不依赖于任何位置的索引 i i i。
练习
(1)假设设计一个深度架构,通过堆叠基于位置编码的自注意力层来表示序列。可能会存在什么问题?
(2)请设计一种可学习的位置编码方法。