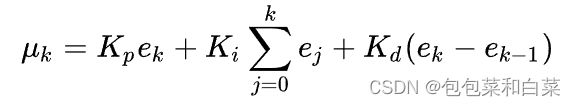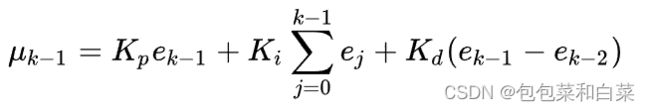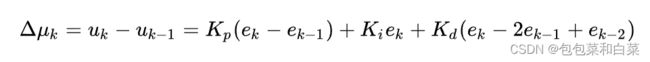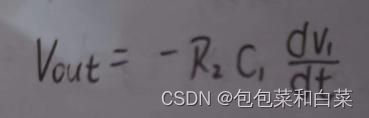基于PSpice的PID控制器的硬件电路仿真
摘 要
pid控制器是所有控制系统中最基础,最简单,也是最普遍的一种控制器,pid算法蕴涵了动态控制中过去、现在、将来的主要信息,其配置几乎是最优,其适应性好,有较强的鲁棒性,对各种工业场合都有不同程度的应用。在实际应用中,软件模拟pid控制器因为其灵活性较好而最为普遍,但软件模拟pid调节较为繁琐,需要更多的调节经验作为功底。本文通过精确的电路仿真结果介绍常见pid控制器中的P控制,PI控制,PD控制及PID控制的电路仿真,再比较几种控制器的优劣,最后分析硬件pid相较于软件模拟pid的优点。
关键词: PSpice仿真,基本运算电路,P控制器,PI控制器,PD控制器, PID控制器
Abstract
Pid controller is the most basic, simplest and most common controller in all control systems. Pid algorithm contains the main information of dynamic control in the past, present and future. Its configuration is almost optimal, with good adaptability and strong robustness, and it has different degrees of application in various industrial situations. In practical application, software simulation PID controller is the most common because of its good flexibility, but software simulation PID adjustment is more complicated, and more adjustment experience is needed as the foundation. This paper introduces the circuit simulation of P control, PI control, PD control and PID control in common PID controller through precise circuit simulation results, and then compares the advantages and disadvantages of several controllers, and finally analyzes the advantages of hardware PID compared with software pid simulation.
Keywords: PSpice simulation, basic operation circuit, P controller, PI controller, PD controller, PID controller
目 录
第1章 绪 论 4
1.1 课题背景 4
1.2 PID算法理论介绍 4
1.2.1 PID算法的发展 5
1.2.2 PID算法的分类 5
1.3 本文的主要研究内容 6
第2章 软件模拟PID算法的简要介绍 6
2.1 增量式PID介绍 6
2.1.1 原理 6
2.1.2 实现过程 7
2.2 位置式PID介绍 7
2.2.1 原理 7
2.3 软件模拟PID控制器的优缺点分析 7
2.4 本章小结 8
第3章 硬件PID控制器的详细分析
3.1 基本运算电路
3.1.1 比例运算电路
3.1.2 加减运算电路 10
3.1.3 积分运算电路.......................................................11
3.1.4 微分运算电路.......................................................12
3.1.5 模拟被控制对象电路.................................................14
3.2 增量式PID控制器分析 15
3.2.1 P控制器 15
3.2.2 PD控制器 17
3.2.3 PID控制器....................................................................................................................................20
3.3 位置式PID控制器分析 22
3.3.1 PID控制器 22
3.4 本章小结 24
结 论
参考文献
第1章 绪 论
-
- 课题背景
自身背景:
模拟电子技术学习并熟练掌握各类基本运算电路的原理,学习了PSpice电路仿真,参与了多种学科竞赛对软件模拟pid算法有较深了解。
外部背景:
PID控制器问世至今己有近70 年历史,它以其结构简单、稳定性好、工作可调整方便而成为工业控制的主要技术之一。控制理论的发展也经历了古典控制理论、现代控制理论和智能控制理论三个阶段。智能控制的典型实例是模糊全自动洗衣机等。自动控制系统可分为开环控制系统和闭环控制系统。一个控制系统包括控制器、传感器、变送器、执行机构、输入输出接 口。控制器的输出经过输出接口、执行机构,加到被控系统上;控制系统的被控量,经过传感器,变送器,通过输入接口送到控制器。pid控制器是所有控制系统中最基础,最简单,也是最普遍的一种控制器,pid算法蕴涵了动态控制中过去、现在、将来的主要信息,其配置几乎是最优,其适应性好,有较强的鲁棒性,对各种工业场合都有不同程度的应用。
-
- PID算法理论介绍
在工程实际中,应用最为广泛的调节器控制规律为比例、积分、微分控制,简称PID控制,又称PID调节。其因结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。当被控对象的结构和参数不能完全掌握,或得不到精确的数学模型时,控制理论的 其它技术难以采用时,系统控制器的结构和参数必须依靠经验和现场调试来确定,这时应用PID控制技术最为方便。即当我们不完全了解一个系统和被控对象,或 不能通过有效的测量手段来获得系统参数时,最适合用PID控制技术。PID控制,实际中也有PI和PD控制。PID控制器就是根据系统的误差,利用比例、 积分、微分计算出控制量进行控制的。PID算法是控制行业最经典、最简单、而又最能体现反馈控制思想的算法。一般来说,设计和实现PID算法是完成自动控制系统的基本要求。首先我们从PID算法最基本的原理开始分析和设计这一经典命题。
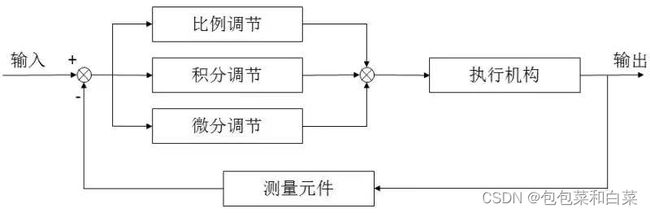
PID算法的执行流程是非常简单的,即利用反馈来检测偏差信号,并通过偏差信号来控制被控量。而控制器本身就是比例、积分、微分三个环节的加和。其功能框图如下:
根据上图我们考虑在某个特定的时刻t,此时输入量为rin(t),输出量为rout(t),于是偏差就可计算为err(t)=rin(t)-rout(t)。于是PID的基本控制规律就可以表示为如下公式: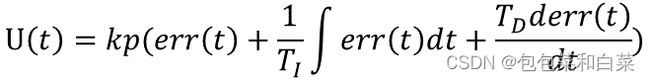
其中Kp为比例带,TI为积分时间,TD为微分时间。PID控制的基本原理就是如此。
1.2.1 PID算法的发展
PID控制器 早在30年代末期就已出现。PID控制器问世至今已有近70年历史,它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一 经过70多年来的不断更新换代,PID控制得到了长足的发展。特别是近年来,随着计算机技术的飞速发展,发生了由模拟PID控制到数字PID控制的重大转变。与此同时还涌现出了许多新型PID控制算法和控制方式。例如,非线性PID控制、自适应控制、最优控制、预测控制、鲁棒控制和智能控制等等。
1.2.2 PID算法的分类
PID算法算是控制系统中最常用的算法之一,由于控制系统的特点不同,对PID响应速度和稳定性的要求也不同。为了适应要求,分为以下几种PID算法
- 增量式PID 增量式PID积分时只对当前误差进行积分,运算量相对较小。
- 位置式PID 位置式PID是将每次误差进行累加作为积分,运算量较大,且每次输出均与过去的状态有关。 缺点为可能引起大幅度超调。
- 积分分离式PID 为了消除稳态误差,常在PID控制中引入积分环节。但在启动、结束或大幅度更改设定值时,积分输出可能会引起较大超调甚至震荡,所以采用了积分分离输出,即在误差较大时屏蔽积分环节,当误差小于一定范围时,引入积分控制,使得偏差较大时确保响应速度 偏差较小时确保精度。
- 微分先行PID 在设定目标点后,目标位置一般会发生阶跃改变,为了消除目标值突然变化带来的抖动,可对测量值进行微分作用,使得设定值的调整变得缓和。
本文主要仿真前两种类型的PID的电路,后两种特殊情况的PID不做过多介绍.
1.3 本文的主要研究内容
本课题的研究内容主要是针对不同种类的PID电路的仿真分析,主要有电路设计,调试,仿真结果展示及其与软件模拟PID算法的对比分析和优劣说明。
第2章 软件模拟PID算法的简要介绍
2.1 增量式PID介绍
2.1.1 原理
增量式PID指数字控制器的输出只是控制量的增量∆uk。当执行机构需要的控制量是增量,而不是位置量的绝对数值时,可以使用增量式PID控制算法进行控制。
2.1.2 实现过程
增量式PID控制算法可以通过位置式PID公式推导出:
- 当前误差采样后的输出值μk:
- 上一次误差采样后的输出值μk-1
- (1)-(2)得:
2.2 位置式PID介绍
2.2.1 原理
位置型 PID 控制算法,适用于不带积分元件的执行器,执行器的动作位置与其输入信 号 呈一一对应的关系。控制器根据第n次被控变量采样结果与设定值之间的偏差 e (n)计算 出 第n次采样之后所输出的控制变量。其与增量式PID较为类似,不同指出在于每次执行完后的当前状态没有整体的累计效应,与过去状态有关的元素仅仅体现在积分项中。
2.3 软件模拟PID控制器的优缺点分析
软件模拟PID相较于PID硬件电路具有简单灵活,适用范围广的特点,
但不易调节,对环境较为敏感,且与软件执行调节周期紧密联系,波动性大,在要求精度高,环境变化剧烈时效果不好。
2.4 本章小结
本章简要介绍软件模拟PID算法的原理,推导过程等。
第3章 硬件PID控制器的详细分析
3.1 基本运算电路
构建PID控制器电路的前提是设计并仿真各种合适的运算电路,在运算电路中,以输入电压作为自变量,输出电压作为函数,当输入电压变化时,输出电压按一定的数学规律变化,即反应各种基本的运算关系。
为更接近实际控制器,仿真时间采用20s。信号源采用较为瞩目的下降沿和上升沿。
3.1.1 比例运算电路
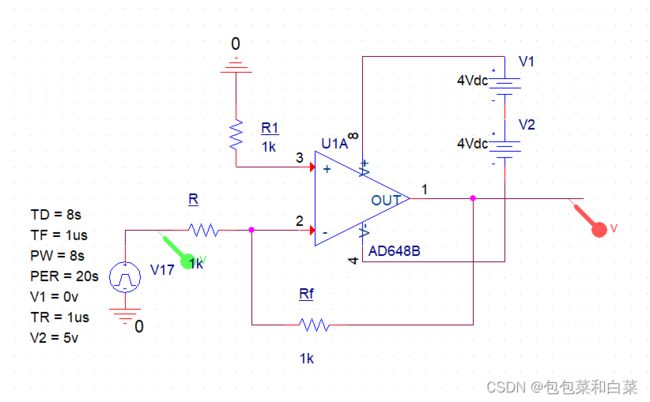
在此设计的基本比例运算电路有正向比例运算电路和反向比例运算电路,其中正向比例运算电路为便于调节比例关系小于1的情况,采用反向比例运算电路再串联一个反相器得到:
设计电路及仿真结果如下:
反向比例电路
电路图
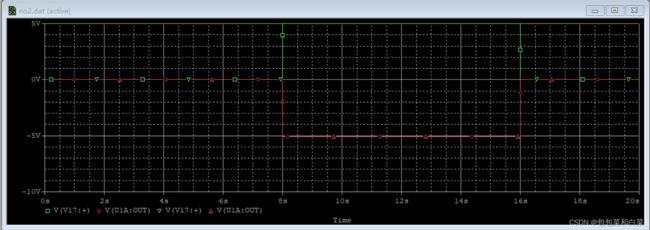
仿真结果
比例系数为-(Rf/R)
同相比例电路
仿真结果
比例系数为(1+R/Rf)
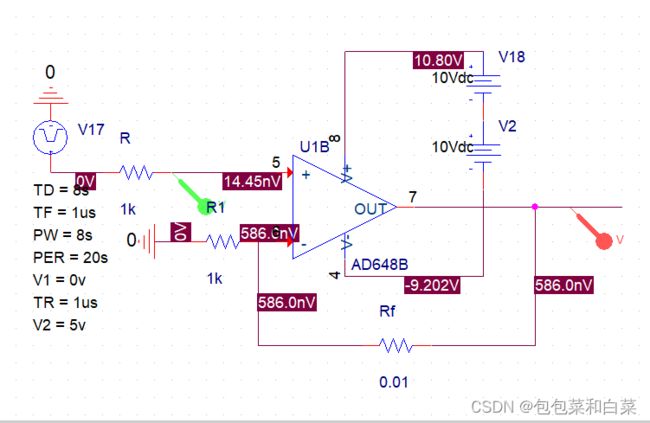
3.1.2加减运算电路
加法运算
电路图
运算关系:Vout=V1+V2
减法运算
电路图
仿真结果
运算关系Vout=V1-V2
3.1.3积分运算电路
电路图
仿真结果
运算关系
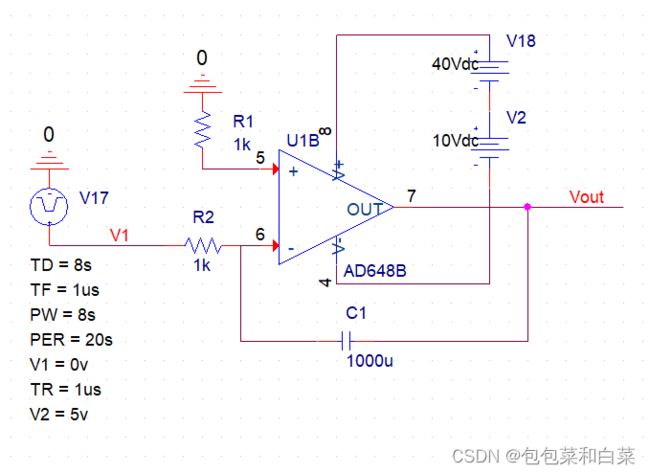
3.1.4 微分运算电路
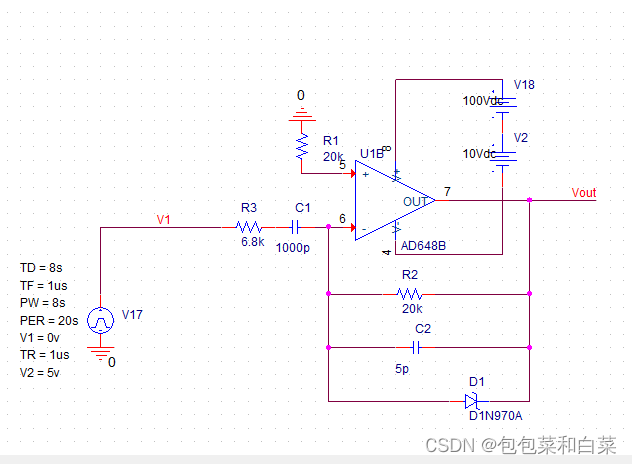
在调试微分运算电路过程中,采用模电教材上的基础微分电路时,仿真结果出现问题,无论输入电压产生阶跃变化,还是脉冲式大幅值干扰,都会使得集成运放内部的放大管进入饱和或者截至状态,以至于即使信号消失,管子还不能脱离原状态回到放大区,出现阻塞现象,电路不难正常工作,且反馈网络具有滞后效应,他与集成运放内部的滞后环节相叠加,易于产生自激振荡,使得电路不稳定。查阅资料得知,这时,在输入端串联一个小阻值的电阻R3,以限制输入电流,也就限制了R2中的电流,在反馈电阻上并联稳压二极管,来限制输出电压幅值,保证集成运放中的放大管一直处于放大区,不至于出现阻塞现象,在R2上并联小容量电容C2,起相位补偿作用,提高电路的稳定性。
电路图
仿真结果
放大图
运算关系
3.1.5 模拟被控制对象电路
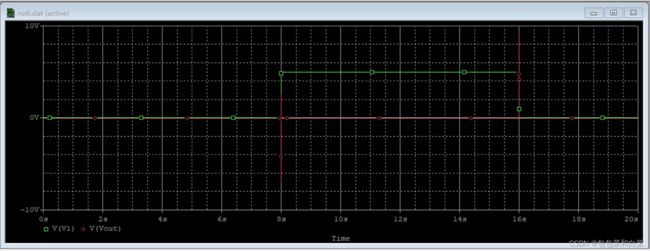
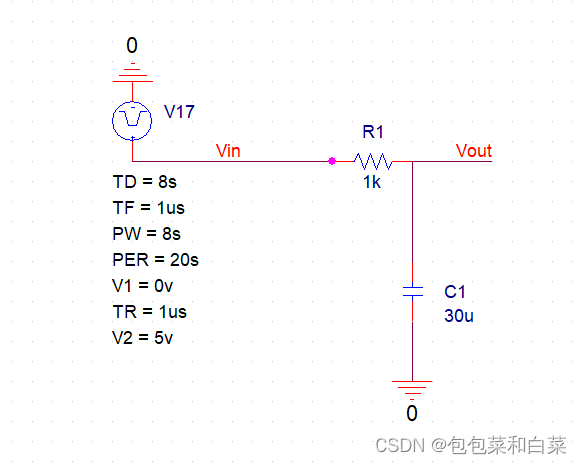
在实际应用中,被控制对象(如电机,舵机,温度加热器等)一般具有一定的滞后现象,例如,当电机接收到一定变速信号时,电机速度变化,而电机速度是一个模拟量,不会跳变,需要一定的时间来变化,而这个时间据被控制对象的不同而不同,具体为100ms到数秒不等。几乎所有的对象的变化趋势都服从一定的趋势,而这个趋势与电容充电时其两端电压最为相似。在这里用电容冲放电来模拟。电路及仿真结果如下:
电路图
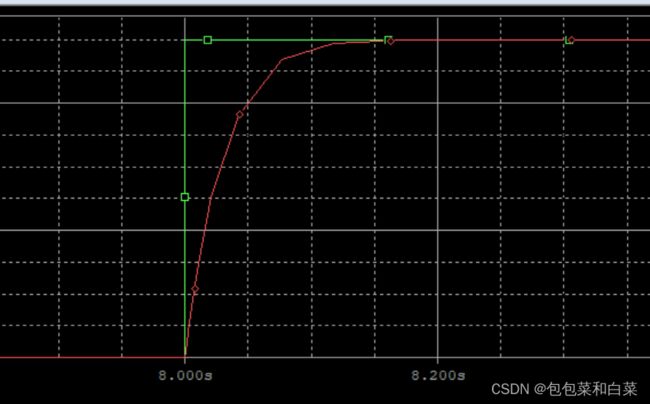
仿真结果
放大图
3.2 增量式PID控制器分析
3.2.1 P控制器
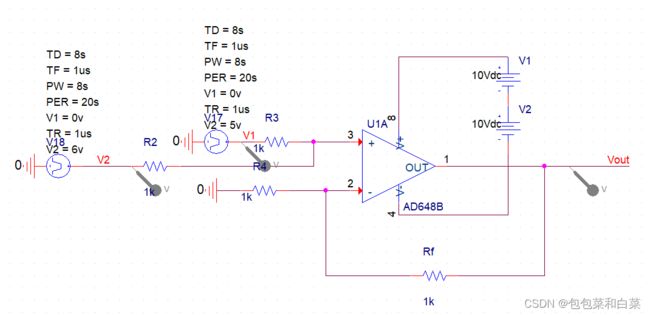
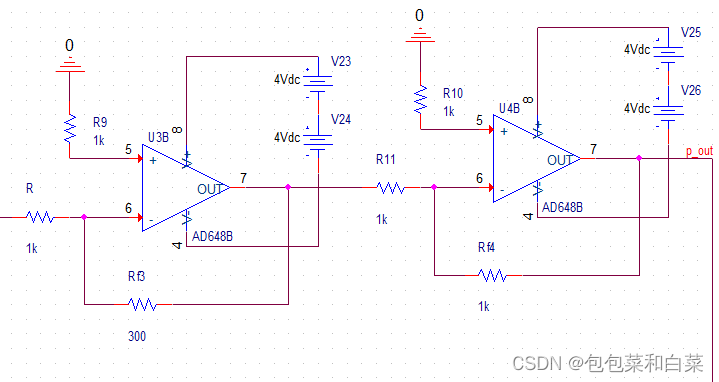
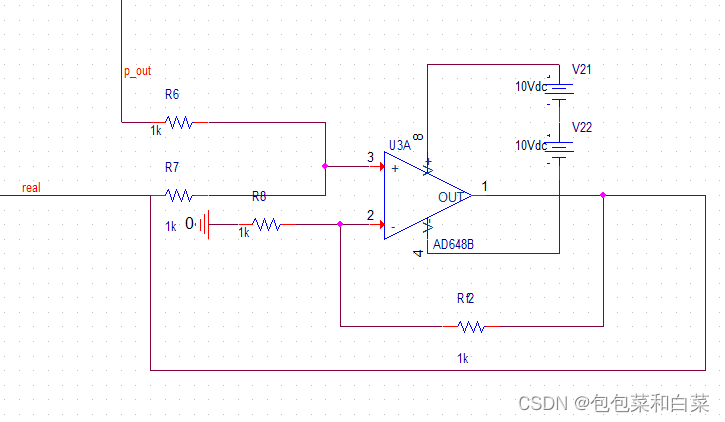
电路各模块:
图3.17中信号源为期望值target,图中减法器实现期望值与真实值(real)的差值(err)输出为err,进入后续图3.18同相比例器(通过两个反向比例器实现,目的是便于调节小于1的比例),经过P运算得到p_out,将此时的p_out与真实值real相加,从而逐渐调节真实值至目标值。
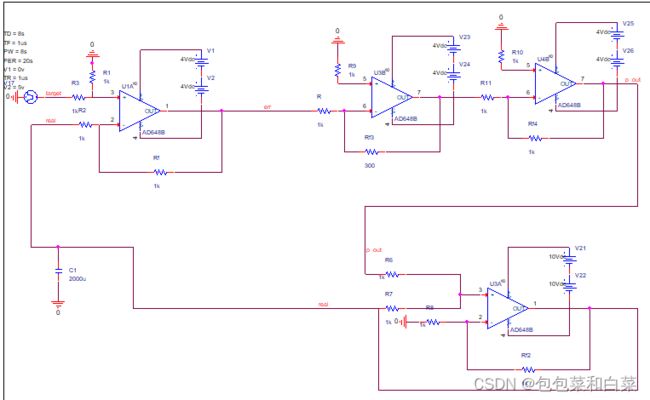
整体电路如图3.20
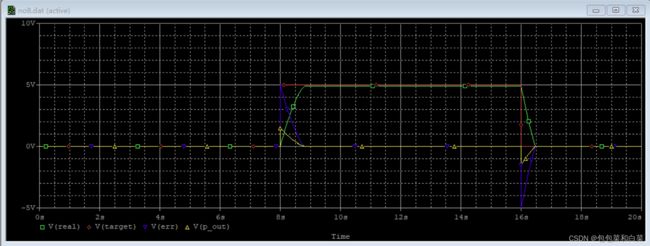
仿真结果如图3.21,3.22,3.23
仿真结果中红线为期望target值,绿线为实际值,蓝线为err值,黄线为p_out值。从图中易发现,当期望值发生上升沿或者下降沿变化时,实际值(绿线)会由于p_out(黄线)的调节逐渐接近期望值(红线),且在此过程中,err值(蓝线)逐渐减小,直至为0。在此过程中,易分析,当同相比例器系数较大时,p_out数值将会变大,这是,real将会更快地到达target值。
3.2.2 PD控制器
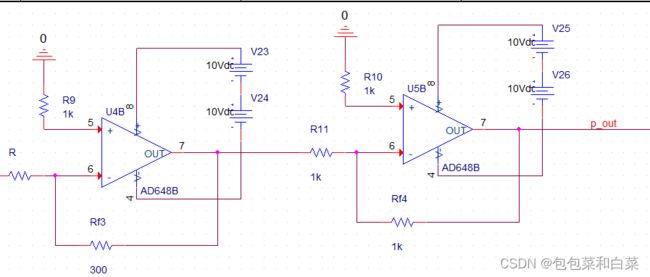
电路各模块:
图3.24中信号源为期望值target,图中减法器实现期望值与真实值(real)的差值(err)输出为err,进入后续图3.25同相比例器(通过两个反向比例器实现,目的是便于调节小于1的比例),经过P运算得到p_out,图3.26为微分器,用来计算d_out,将此时的p_out,d_out与真实值real相加,从而逐渐调节真实值至期望值。当真实值逐渐接近期望值时,p_out和d_out逐渐减小最终趋于0.
整体电路:
图3.28中微分器串联一个反相器是为了保证极性一致,即预测err过去的变化,将对过去的预测加到现在的d_out上,最终再加到真实值上,实现现在真实值的快速变化,最终是的real更大变化率的趋近期望值target。
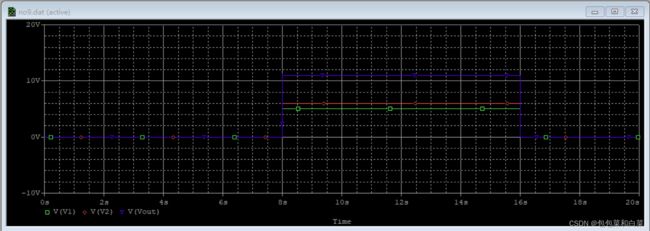
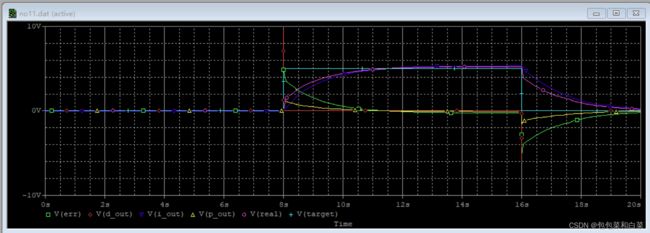
仿真结果:
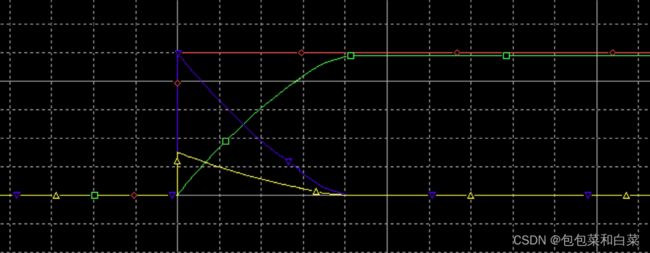
途中绿线为真实值与期望值的差err值,红线为微分部分的输出值d_out,蓝线为P比例部分的计算输出值p_out值,黄线为真实值real,紫线为目标target值。由图3.31可以看出,当期望值发生上升沿时,在一瞬间err值发生突变,其微分d_out(红线)将会有较大变化,同时将此结果d_out与p_out一起加到real上,最终得到现在状态+过去预测共同调节真实值趋近期望值。
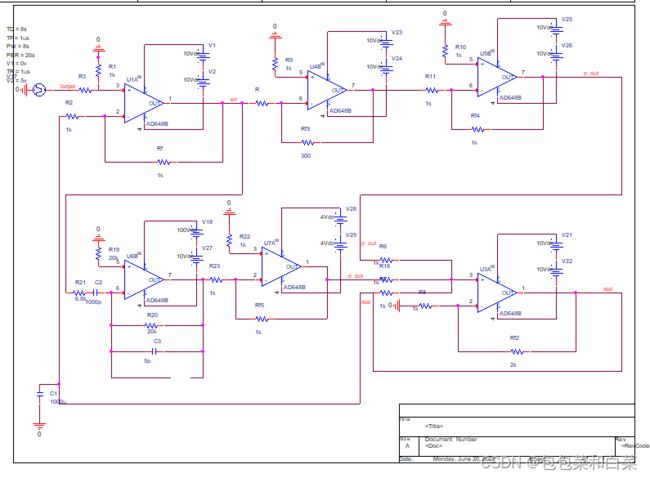
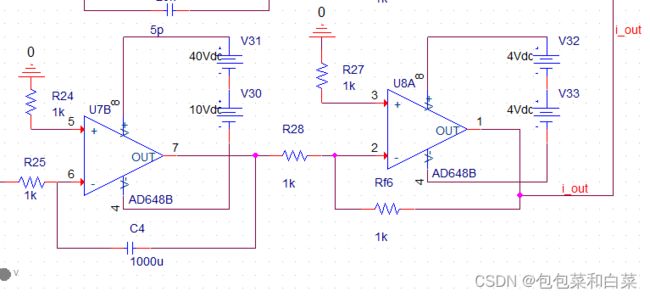
3.2.3 PID控制器
各模块介绍:
比例模块,信号源模块,加减运算模块,微分模块与以上类似,在此部分不再赘述,一下时积分模块:
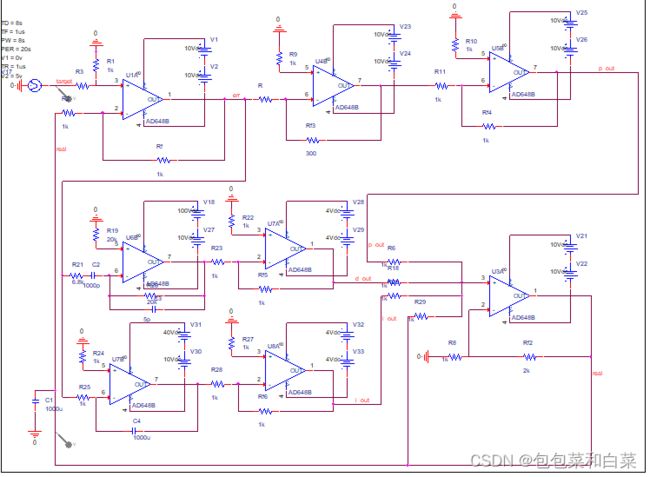
整体电路图:
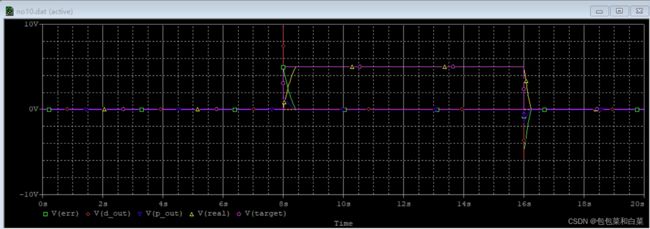
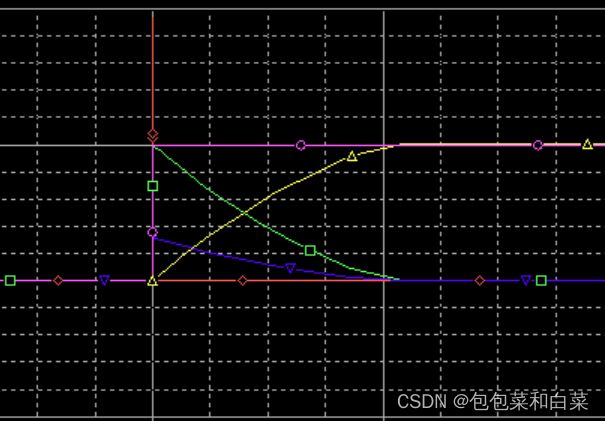
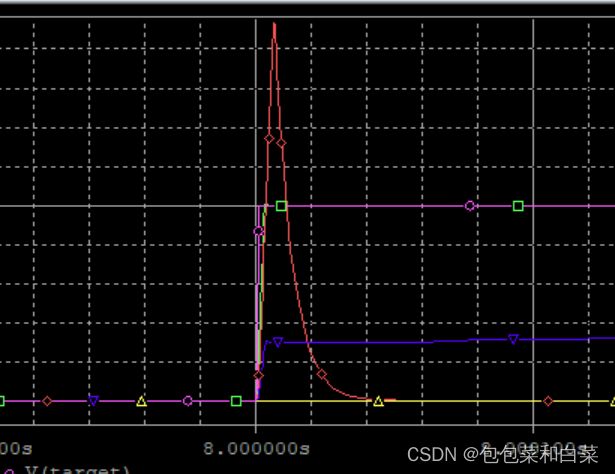
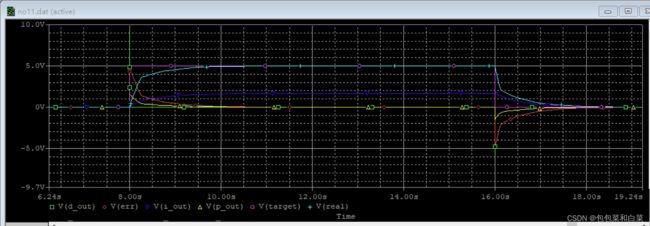
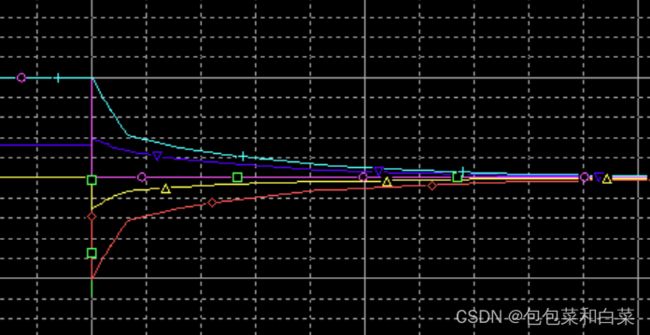
仿真结果:
仿真结果中,紫色线为期望值target,蓝线为实际值real,黄线为比例器输出p_out,绿色线为微分器输出d_out,蓝紫色线为积分项输出i_out,红线为误差值err。可以看出,当err值不为零时,i_out出现累加积分,且逐渐增大,作用在real上,使得真实值更接近期望值,且与过去所有状态有关,i_out由过去所有状态决定,整体电路实现了过去,现在,将来三种作用的共同控制被控制量。
3.3 位置式PID控制器分析
3.3.1 PID控制器
对于位置式PID控制器,其与增量式较为类似。增量式是在位置式的基础上做了误差的累积,而位置式的输出只与当前的p_out,d_out,i_out有关,与过去的联系只与i_out有关。其控制与增量式的区别体现在:响应速度慢,但不易出现过调,效果稳定。
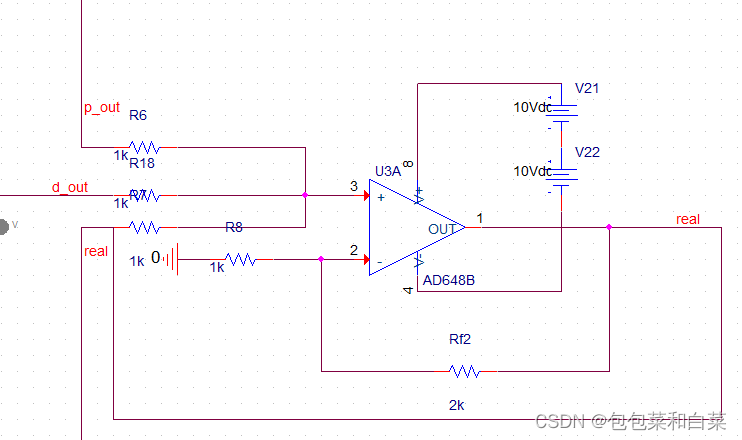
电路图如下:
整体电路图与增量式类似,不同之处是位置式没有了增量式中的将实际值也一并加入加法器(上图中U3A,在电路图右下角),即此时直接将P,I,D三个部分输出的和加起来作为实际值。
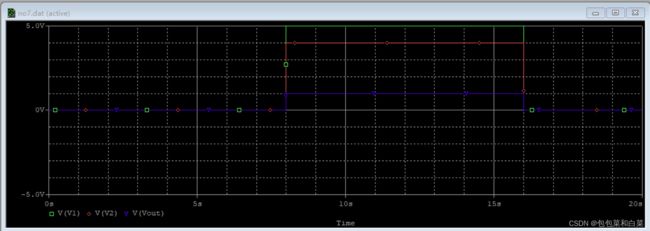
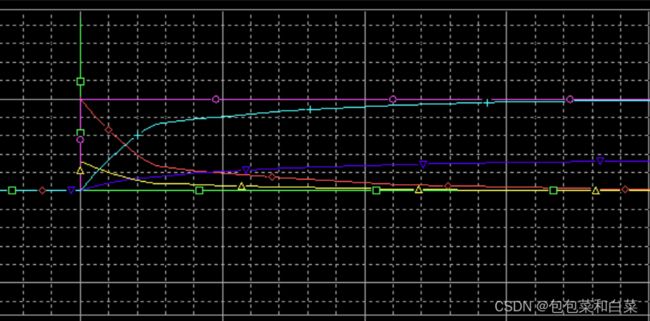
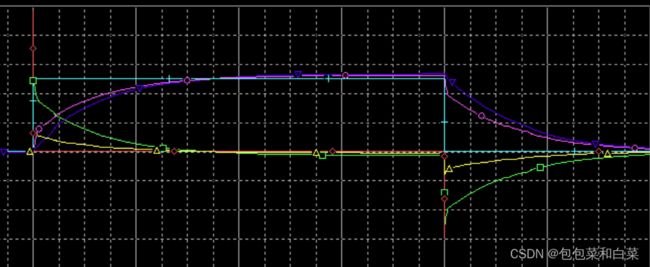
仿真结果:
图3.38
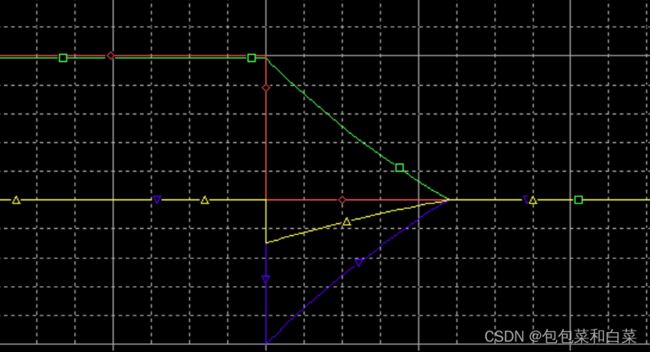
由仿真结果,对比实际值real(紫红色线)和期望值target(浅蓝色线),位置式PID与增量式PID相比,其响应速度明显变慢,各个输出的变化速度明显放缓。
整体作用效果为,比例项和微分项将真实值拉近期望值,但此时两者并不会相等,即出现稳态误差,但随着时间的积累,此误差积分得到的i_out将会逐渐增大,从而将此误差消除。最终实现真实值real趋近期望值target。
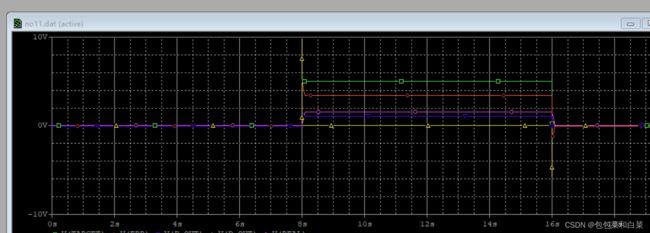
对与位置式pid,积分项是必要的,如果没有积分项,将会出现较大的稳态误差,仅仅有比例项和微分项不会将此误差消除。在没有积分项时,仿真结果如下:
图3.40
图3.41
仿真结果中,粉红色线为真实值real,绿色线为期望值target,不难发现,真实值与期望值还有明显的差距。这种情况可以通过增大比例器的参数大小来减小这个误差,但这个稳态误差会一直存在。因此,积分项是必要的。
3.4 本章小结
本章首先介绍了设计PID控制器中的各个运算模块。接着依次分析了增量式PID控制器的P控制器,PD控制器,PID控制器和位置式PID控制器,并分析了他们之间的差异。
结 论
本文简要介绍了软件模拟PID算法的原理及实现过程,再详细设计并对比分析了多种PID控制器硬件电路。取得了可观的效果,我们明显可以看出,硬件PID具有易调节,效果比软件更加完美,且不具有超调,震荡等软件PID模拟易出现的问题,PID硬件电路中的各个调节量均为模拟量,因而可以连续实时根据当前电路中的任意部分而变化,且这个变化是连续的,因此他不具有软件模拟PID中不可比年的震荡现象,硬件PID电路与软件模拟PID电路最本质的区别是模拟量调节被控制量和数字量调节被控制量的区别。软件调节具有周期性调节的特点,而PID硬件电路可理解为调节周期极短软件调节。这也就体现了硬件PID的优越性。
通过PSpice对各种运算电路设计,仿真,以及设计调试各种PID控制器电路。巩固了所学的模拟电子技术的基础知识和cad仿真分析。
参考文献
1.普通图书
[1]华成英.模拟电子技术基础第五版.高等教育出版社,2015:276-339.
[2]胡寿松.自动控制原理第五版.高等教育出版社,2009.
[3]刘金琨.先进pid控制MATLAB仿真第三版.高等教育出版社,2020.
2.学位论文
[1]刘敏.Orcad在通信电子线路教学中的应用.2014.20.013
[2]蔡超波.PSpice电路仿真在电路原理中的应用.2019.3
- 其他
[1]CSDN.30539835 . PID算法原理及基本实现.2018.4.21
[2]CSDN.z小旋.位置式PID与增量式PID区别浅析.2019.4.26
[3]CSDN.奇妙水果.位置式PID与增量式PID理论推导.2021.5.28
[4]CSDN.假如明天.增量式PID分析及参数整定.2017.1.16
[5]CSDN.永远滴神yyds.积分和微分电路结构原理带Multisim仿真.2021.4.8
[6]哔哩哔哩.421施工队.从不懂到会用,PID从理论到实践.2021.5.24
[7]百度文库.基本运算电路仿真.2019.7.18