10大排序算法之四：归并排序【稳定的】，复杂度中，系统常用归并排序

10大排序算法之四：归并排序【稳定的】，复杂度中，系统常用归并排序

提示：整个算法界，一共有十大排序算法，每一个算法都要熟悉，才算是算法入门

算法界的十大排序算法分别是：
选择排序、冒泡排序、插入排序、堆排序、希尔排序、归并排序、快速排序、桶排序、计数排序，基数排序。
（1）选择排序：10大排序算法之一：选择排序【不稳定】，一般不用选择排序的
（2）冒泡排序：10大排序算法之二：冒泡排序【稳定的】，但复杂度高，一般不用冒泡排序的
（3）插入排序：10大排序算法之三：插入排序【稳定的】，复杂度高，系统常在数据少时用插入排序。

如果你想进互联网大厂，至少这上面的其中最重要的8种，是必须熟练掌握的：
去掉希尔排序，希尔排序是一种改进的插入排序算法——所以只需要掌握插入排序
桶排序中最重要的就是计数排序和基数排序，都是桶的思想

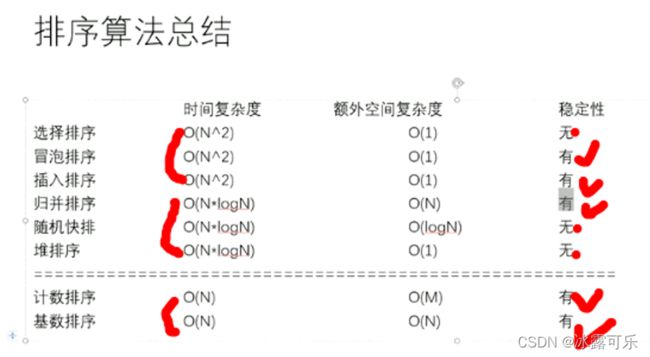
根据算法复杂度低一点的，又稳定的
咱们可以最常用的算法实际上就四种：
插入排序（o(n^2)）【当数据量小时，这个方法简单】【稳定】、
堆排序o(nlog(n))【不稳定】、
归并排序o(nlog(n))【稳定】，
快速排序o(nlog(n))（虽然快排不稳定，但是很多不需要稳定情况下，快排非常快）
因此，o(n)的桶排序很少用，除非面试官特别申明，否则都用比较排序。
归并排序是最常用的，复杂度低，而且稳定，达到了一个非常好的折中。

---

题目

请你手撕插入排序的算法代码，要求将arr中的数字升序排序。

---

一、审题

示例：arr = 5 3 1 8 6 2 4
让其最终变为：arr= 1 2 3 4 5 6 8

---

二、归并排序

归并排序的思想：
之前咱们学过递归思想的时间复杂度用master公式来求：
递归思想求arr中最大值，递归函数先调用处理几部分，然后整理和归并信息返回

运用递归思想，将arr分为L–mid–R两部分，先排序左边，先排序右边，再归并左右2部分，最终让L–R上有序
比如，案例中的arr
（1）递归分成0–3和4–6两部分
（2）0–3又分为0–1,2–3两部分，4–6又分为4–5,6–6两部分
base case：遇到一个元素，直接返回，不操作
（3）此时0和1位置都是独立有序的，所以归并arr中L–mid，mid+1–R两部分，merge(arr,L,mid,R)使得L–R上整体有序。
看下图：

（4）归并函数：merge(arr,L,mid,R)咋做呢？
双指针，p1指向L，p2指向mid+1，比较p1和p2，谁小，先复制谁？用help缓存起来
当一边复制完了以后，还剩下元素那边直接放到help屁股
最后将help转移还给arr的L–R中，可见help就是R-L+1这么长的缓存数组

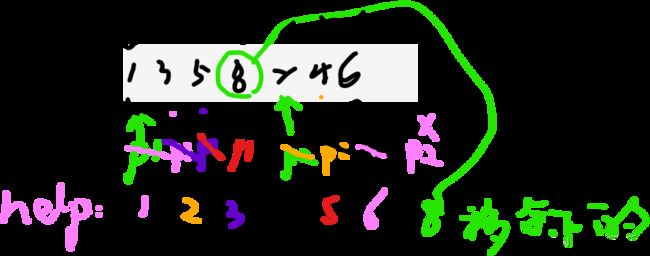
看一个案例：上面有一次左右递归排序之后，arr=1 3 5 8 2 4 6
L=0，mid=3，R=6
因此调用merge(arr,L, mid, R)=merge(arr,0,3,6)
（1）p1=L=0，p2=mid+1=4，对比[p1]<[p2],先搬1，p1++=1；
（2）对比[p1]>[p2],先搬2，p2++=5；
（3）对比[p1]<[p2],先搬3，p1++=2；
（4）对比[p1]>[p2],先搬4，p2++=6；
（5）对比[p1]<[p2],先搬5，p1++=3；
（6）对比[p1]>[p2],先搬6，p2++=7；
此时，p2已经越界，超过R了
所以停止
看左边还没有搬完呢，将左边剩下的所有，8搬到help后边
然后将help转移给arr的L–R上

手撕代码：
归并排序，宏观调度室是：左右两部分递归排序，排序好的俩有序数组，用来归并成一个有序数组，放回L–R上

//归并排序，复习
    //首先，准备merge L--mid--R上归并，这个很重要！！！
    public static void mergeReview(int[] arr, int L, int mid, int R){
        if (L >= R) return;
        //归并是至少俩个以上的元素，help转移

        int[] help = new int[R - L + 1];//这么长
        int p1 = L;
        int p2 = mid + 1;
        //先merge，小的在前，大的在后，相对位置不变
        int i = 0;//用来给help索引的
        while (p1 <= mid && p2 <= R){
            help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];//i每次增，谁小先搬谁，然后p++
        }
        //然后二选一，把剩下那个部分全部copy给help
        while (p1 <= mid) help[i++] = arr[p1++];
        while (p2 <= R) help[i++] = arr[p2++];

        //最后把help转移给arr
        for (int j = 0; j < help.length; j++) {
            arr[L + j] = help[j];//从L开始放
        }
    }

    //有了merge这个函数，我们就可以用递归思想，做归并排序了
    public static void mergeSortReview(int[] arr, int L, int R){
        //2个以上，就可以排序
        //base case
        if (L == R) return;

        //先递归排序左右两部分，然后归并排序
        int mid = L + ((R - L) >> 1);
        mergeSortReview(arr, L, mid);
        mergeSortReview(arr, mid + 1, R);

        mergeReview(arr, L, mid, R);//归并排序
    }

测试：

//常用的交换数组函数
    public static void swap(int[] arr, int i, int j){
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

    //对数器之构建随机数组
    public static int[] createArray(int arrSize, int maxValue){
        int[] arr = new int[arrSize];
        for (int i = 0; i < arrSize; i++) {
            arr[i] = (int)(maxValue * Math.random());//0-N-1的随机数
        }
        return arr;
    }

    public static void checker(){
        //生成检验数组
        int[] arr = createArray(10000,10000);
        int[] arr2 = new int[arr.length];//赋值同样一个数组arr
        for (int i = 0; i < arr.length; i++) {
            arr2[i] = arr[i];//copy即可
        }
        int[] arr3 = new int[arr.length];//赋值同样一个数组arr
        for (int i = 0; i < arr.length; i++) {
            arr3[i] = arr[i];//copy即可
        }

        //绝对的正确方法——暴力方法，或系统函数，操作arr
        Arrays.sort(arr);
        //优化方法，操作arr2
        mergeSort(arr2, 0, arr2.length-1);//从0-len-1做归并排序
        mergeSortReview(arr3, 0, arr3.length-1);//从0-len-1做归并排序

        //然后两个数组对位校验
        boolean isSame = true;
        for (int i = 0; i < arr.length; i++) {
            if(arr[i] != arr2[i]) {
                isSame = false;
                break;//只要有一个不等，不必继续判断了
            }
        }
        System.out.println(isSame == false ? "oops,wrong!" : "right!");
        System.out.println();
        isSame = true;
        for (int i = 0; i < arr.length; i++) {
            if(arr[i] != arr3[i]) {
                isSame = false;
                break;//只要有一个不等，不必继续判断了
            }
        }
        System.out.println(isSame == false ? "oops,wrong!" : "right!");
    }

//有了递归思想以后，就可以左右划分做递归排序和融合
    //递归终止条件：当L=R时，return；
    //否则，左边做递归排序，右边做递归排序
    //最后，merge融合放进help数组，merge是亮点，两个轴处于L和mid+1处，双双对比，谁小放左边。
    // 最后全部copy返回给arr

    public static void main(String[] args) {
        checker();//对数器校验
    }

结果：

right!

right!

归并排序的归并那一步merge函数，很重要，在今后很多经典大厂的面试题中，都会用的。

---

归并排序的时间复杂度

之前讲过递归思想的时间复杂度计算master公式，必须死记硬背的：
今天再说一遍：
如果递归调用a次（归并排序就是典型的a=2次，左右）；
每一次调用规模为N/b，归并排序的b=2
除了递归的复杂度之外，还有merge的复杂度，既然i++，则就是o(n)的复杂度，即o(n^d)=o(n)，故d=1
所以有这么一个关系：

归并排序中a=2，b=2，d=1
所以：归并排序的时间复杂度为o(nlog(n))

懂了吧！

---

总结

提示：重要经验：

1）归并排序的核心思想，先把arr的L–R上分为2部分，然后再归并这俩有序数组为一个整体有序数组
2）自然用master公式计算得知，归并排序的时间复杂度为o(nlog(n))