【详解+推导!!】蒙特卡洛方法、接受拒绝采样、重要性采样、MCMC方法
蒙特卡洛方法、接受拒绝采样、重要性采样、MCMC方法
文章目录
- 一、蒙特卡洛方法
-
- 1. 什么是蒙特卡洛方法
- 2. 蒙特卡洛积分推导
- 3.python实例
- 承上启下
- 二、接受-拒绝采样
-
- 1. 核心思想介绍
- 2. 例子
- 三、重要性采样
-
- 1. 普通重要性采样
- 2. 方差分析
- 3. 加权重要性采样
- 四、MCMC方法
-
- 1. 马氏链平稳分布
- 2. 平稳分布判定:细致平稳条件
- 3. 构造状态转移概率矩阵 P P P
- 4. MCMC的算法步骤
- 5. Metropolis-Hastings采样方法
- 最后推荐几篇相关文章:
一、蒙特卡洛方法
1. 什么是蒙特卡洛方法
蒙特卡罗方法也称统计模拟方法,以概率为基础的方法,与它对应的是确定性算法,其核心思想是使用采样+平均(随机近似)的方式去估计出无法计算的值。
蒙特卡洛方法的一个重要应用就是求定积分。来看下面的一个例子。
2. 蒙特卡洛积分推导
I = ∫ a b g ( x ) d x I=\int_{a}^{b} g(x)dx I=∫abg(x)dx
其中被积函数 g ( x ) g(x) g(x)在 [ a , b ] [a,b] [a,b]内可积,我们选择一个概率密度函数为 f X ( x ) f_X(x) fX(x)的方式进行采样,并且保证在 [ a , b ] [a,b] [a,b]内该采样函数的概率和为1,即 ∫ a b f X ( x ) d x = 1 \int_{a}^{b} f_X(x)dx = 1 ∫abfX(x)dx=1,那么原积分可写成:
I = ∫ a b g ( x ) f X ( x ) f X ( x ) d x = ∫ a b g ( x ) f X ( x ) d x ⋅ ∫ a b f X ( x ) d x = ∫ a b g ( x ) f X ( x ) d x \begin{aligned} I&=\int_{a}^{b} \frac{g(x)}{f_X(x)} f_X(x) dx \\ &=\int_{a}^{b} \frac{g(x)}{f_X(x)} dx \cdot \int_{a}^{b} f_X(x) dx \\ &=\int_{a}^{b} \frac{g(x)}{f_X(x)} dx \end{aligned} I=∫abfX(x)g(x)fX(x)dx=∫abfX(x)g(x)dx⋅∫abfX(x)dx=∫abfX(x)g(x)dx
我们以概率密度函数 f X ( x ) f_X(x) fX(x)的方式进行采样,得到 N N N个样本,则可以将上面的式子写成离散形式:
I ′ = 1 N ∑ i = 1 N g ( x i ) f X ( x i ) I' = \frac{1}{N} \sum_{i=1}^{N} \frac{g(x_i)}{f_X(x_i)} I′=N1i=1∑NfX(xi)g(xi)
则有 I ′ ≈ I I' \approx I I′≈I
上面的例子其实就是取 f X f_X fX为均匀分布:
f X ( x ) = 1 b − a , a ≤ x ≤ b f_X(x) = \frac{1}{b-a},a \leq x \leq b fX(x)=b−a1,a≤x≤b
带入我们最终推导出来的式子即:
I ′ = b − a N ∑ i = 1 N g ( x i ) I' = \frac{b-a}{N} \sum_{i=1}^{N} g(x_i) I′=Nb−ai=1∑Ng(xi)
3.python实例
首先看一个经典的用蒙特卡洛方法求 π \pi π值。
import random
def calpai():
n = 1000000
r = 1.0
a, b = (0.0, 0.0)
x_neg, x_pos = a - r, a + r
y_neg, y_pos = b - r, b + r
count = 0
for i in range(0, n):
x = random.uniform(x_neg, x_pos)
y = random.uniform(y_neg, y_pos)
if x*x + y*y <= 1.0:
count += 1
print (count / float(n)) * 4
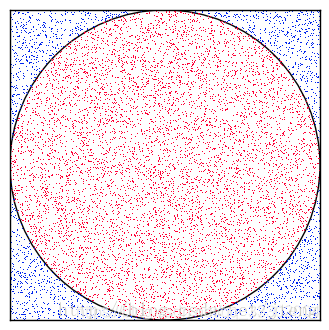
正方形内部有一个相切的圆,它们的面积之比是 π / 4 \pi/4 π/4。现在,在这个正方形内部,随机产生 n n n个点,计算它们与中心点的距离,并且判断是否落在圆的内部。若这些点均匀分布,则圆周率 π = 4 ∗ c o u n t / n \pi=4 * count/n π=4∗count/n, 其中 c o u n t count count表示落到圆内投点数 n n n表示总的投点数。
承上启下
从上面的介绍中我们可以看出蒙特卡洛方法非常直观,但是实际中样本的概率分布 f X f_X fX[ 后面我们以 p ( x ) p(x) p(x)表示样本点的概率分布 ]往往十分复杂,我们很难采样出符合这个概率分布的一组样本。
为了解决概率分布 p ( x ) p(x) p(x)复杂,难以采样的问题派生出了两种解决方案,分别为:接受-拒绝采样和重要性采样。这两种方法都是基于一个事实,目标分布 p ( x ) p(x) p(x)无法直接采样,于是引入一个提议分布 q ( x ) q(x) q(x)来辅助采样。所谓提议分布就是一个我们已知的,很好采样的分布,例如:均分分布、高斯分布等。
二、接受-拒绝采样
1. 核心思想介绍
这里我们介绍最基本的接受-拒绝采样方法,目标是根据给定的概率密度函数 p ( x ) p(x) p(x)产生服从该分布的样本集 X X X。
基本思想是利用一个易于采样的提议分布 q ( x ) q(x) q(x),例如高斯分布,进行采样,而后再对利用 q ( x ) q(x) q(x)得到的样本进行加工,接受符合 p ( x ) p(x) p(x)分布的样本,拒绝不符合 p ( x ) p(x) p(x)分布的样本。
2. 例子
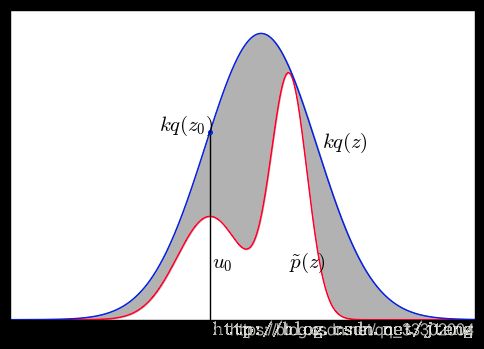
首先我们已知一个复杂分布 p ( x ) p(x) p(x);再取一个提议分布 q ( x ) q(x) q(x)(这里取高斯分分布,图中的变量为 z z z,我文字描述中为 x x x);随后确定一个常量 k k k,保证满足 k q ( x ) ≥ p ( x ) kq(x) \geq p(x) kq(x)≥p(x),在保证上式成立的情况下常量 k k k尽可能取小一些。绘制出图像如下图所示,蓝色为 k q ( x ) kq(x) kq(x),红色为 p ( x ) p(x) p(x)。
采样过程:
① 首先利用 q ( x ) q(x) q(x)采样得到一个样本点 x 0 x_0 x0;
② 再在 [ 0 , k q ( x 0 ) ] [0, kq(x_0)] [0,kq(x0)]区间内进行均匀采样,得到 μ 0 \mu_0 μ0;
③ 判断:若 μ 0 < p ( x ) \mu_0 < p(x) μ0<p(x),则接受该样本,否则拒绝。
采样结果分布图:
由上图可知,该方法可以采样出已知概率分布的样本集。
三、重要性采样
1. 普通重要性采样
回顾一下:我们已知 f ( x ) f(x) f(x),其中 x ~ p ( x ) x~p(x) x~p(x),我们计算 f ( x ) f(x) f(x)的期望如下:
E [ f ( x ) ] = ∫ f ( x ) p ( x ) d x ≈ 1 N ∑ i = 1 N f ( x i ) E[f(x)] = \int f(x)p(x)dx \approx \frac{1}{N} \sum_{i=1}^{N}f(x_i) E[f(x)]=∫f(x)p(x)dx≈N1i=1∑Nf(xi)
上式中的 x i x_i xi按照 x ~ p ( x ) x~p(x) x~p(x)的方式进行采样,即可计算出 E [ f ( x ) ] E[f(x)] E[f(x)]的近似值。
如果 p ( x ) p(x) p(x)比较复杂无法完成采样,这时候我们借助一个简单的提议分布 q ( x ) q(x) q(x)来完成采样,则期望的计算变成如下的样子:
E [ f ( x ) ] = ∫ f ( x ) p ( x ) q ( x ) q ( x ) d x ≈ 1 N ∑ i = 1 N f ( x i ) p ( x i ) q ( x i ) E[f(x)] = \int f(x) \frac{p(x)}{q(x)} q(x) dx \approx \frac{1}{N} \sum_{i=1}^{N}f(x_i)\frac{p(x_i)}{q(x_i)} E[f(x)]=∫f(x)q(x)p(x)q(x)dx≈N1i=1∑Nf(xi)q(xi)p(xi)
上面式子中的 p ( x ) p(x) p(x)和 q ( x ) q(x) q(x)都是已知的,所以便可以利用这个公式计算出 f ( x ) f(x) f(x)的期望,并且由推导可知该积分估计是无偏估计。
我们定义重要性权重: ω i = p ( x i ) q ( x i ) \omega_i = \frac{p(x_i)}{q(x_i)} ωi=q(xi)p(xi),则可以写出普通重要性权重的积分估计方程:
E [ f ( x ) ] ≈ 1 N ∑ i = 1 N ω i f ( x i ) E[f(x)] \approx \frac{1}{N} \sum_{i=1}^{N} \omega_i f(x_i) E[f(x)]≈N1i=1∑Nωif(xi)
2. 方差分析
所谓无偏估计是指重要性采样计算得到的期望估计值等于真实的期望,这一点从推导过程中可以看出来,这也是我们可以用重要性采样的依据。下面我们来分析一下方差,方差的计算公式为:
D ( x ) = E ( x 2 ) − E ( x ) D(x) = E(x^2)-E(x) D(x)=E(x2)−E(x)
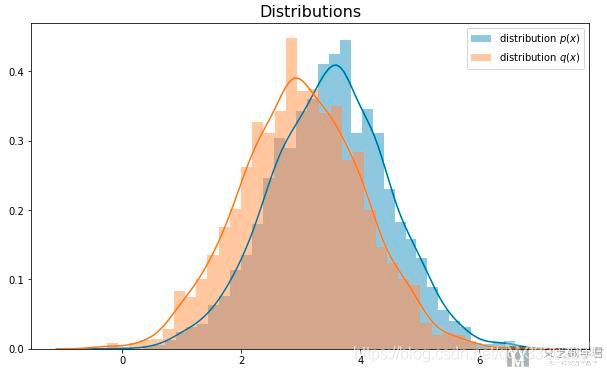
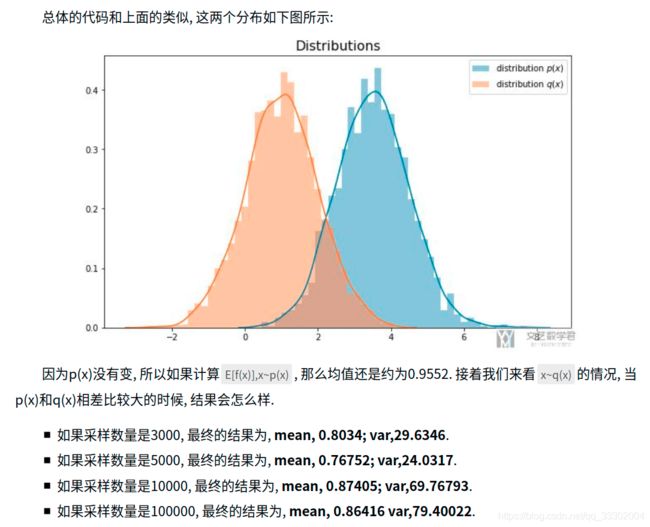
这里的 x x x是对应的是 p ( x ) q ( x ) f ( x ) \frac{p(x)}{q(x)} f(x) q(x)p(x)f(x),由此可以看出如果 p ( x ) q ( x ) \frac{p(x)}{q(x)} q(x)p(x)很大,那么方差也会很大,理论上方差可以达到无穷大。所以当 p ( x ) p(x) p(x)和 q ( x ) q(x) q(x)差异很大的时候,方差会变大,二者比较接近的时候,方差会比较接近真正的方差。下面我们来举个实际的例子。
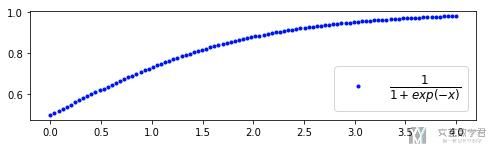
我们定义: f ( x ) = 1 1 + e x p ( − x ) f(x)= \frac{1}{1+exp(-x)} f(x)=1+exp(−x)1,其函数图像如下:
由此我们可以看出来,如果 p ( x ) p(x) p(x)和 q ( x ) q(x) q(x)差异较大,我们就需要做更多的采样才能获得比较准确的期望估计,并且会导致估计的方差较大。
3. 加权重要性采样
加权重要性采样是一种减少重要性采样积分方差的方法,公式如下:
E [ f ] ≈ ∑ n = 1 N ω n ∑ m = 1 N ω m f ( x n ) E[f] \approx \sum_{n=1}^N \frac{\omega^n}{\sum_{m=1}^N \omega^m} f(x^n) E[f]≈n=1∑N∑m=1Nωmωnf(xn)
四、MCMC方法
MCMC是指马尔科夫链蒙特卡洛(Markov Chain Monte Carlo)方法,被视为二十世纪Top10的算法,正是MCMC方法的提出使得许多贝叶斯统计问题的求解成为可能。
当采样空间的维数比较高时,“接受-拒绝采样”和“重要性采样”都不适用,原因是当维数升高时很难找到适合的提议分布,采样效率比较差。而MCMC算法不需要提议分布,只需要一个初始样本点,后面的样本点会依据当前样本点随机产生。
这里需要马尔科夫链中的一些术语和知识可以参考:https://blog.csdn.net/qq_33302004/article/details/115027798
本节会先介绍一些定理和知识,最后再讲解MCMC的采样过程,如果不能理解基础定理的话很难理解MCMC方法,大家耐心理解,也可以看一下后面我的引用文章。
1. 马氏链平稳分布
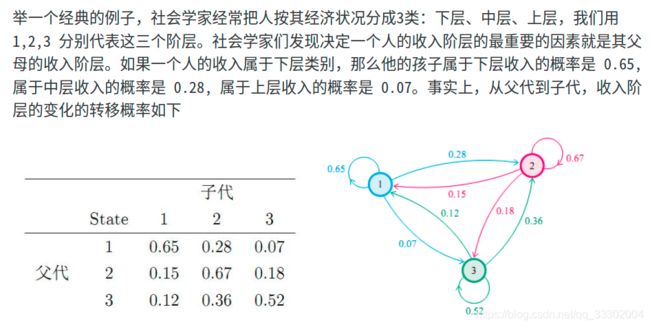
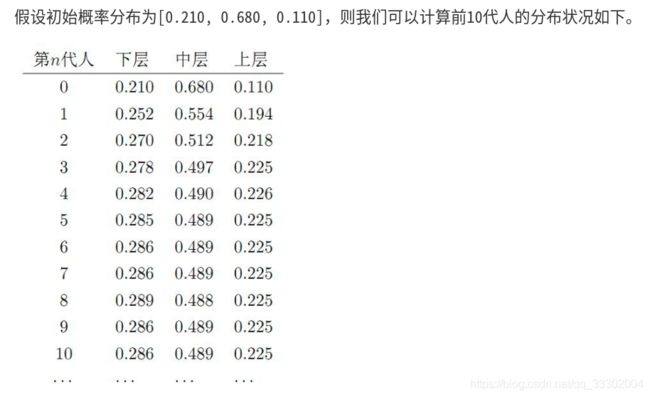
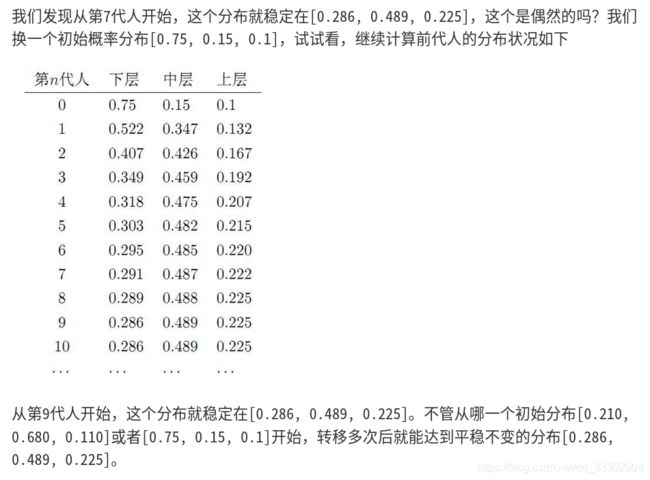
先举例子再讲公式:
由此我们可以看出马尔科夫链最终的稳定分布和初始状态无关,只与状态转移概率矩阵 P P P有关。
我们的目标分布 π \pi π这个就是最终的稳定分布,专业一点表述就是我们本小节的小标题马氏链平稳分布。我们也可以知道,目标分布 π \pi π是由状态转移概率矩阵 P P P决定的。
用数学方式描述马氏链平稳分布:
其背后蕴含的意义:
- 任意两个状态连通并非指状态i可以一步转移到j,而是指状态i可以通过有限的次数转移到j。
- 状态转移矩阵自乘多次转移后,会得到一个稳定值。
- 马氏链稳定后,所有状态i转移到状态j的概率之和是稳定的。
- 一个状态转移矩阵 P P P只有唯一一个对应的稳定分布 π ( x ) \pi(x) π(x)
2. 平稳分布判定:细致平稳条件
假设我们已知一个状态概率分布 π \pi π,如何判定它是否是一个状态转移概率矩阵 P P P的稳定分布呢?这里就用到了细致平稳条件。
如果状态转移矩阵 P P P和分布 π \pi π满足细致平稳条件,则这个分布 π \pi π就是该状态转移矩阵 P P P对应的稳定分布。细致平稳条件定义如下:
π ( i ) p i j = π ( j ) p j i , for all i, j \pi(i) p_{ij} = \pi(j) p_{ji}, \text{ for all i, j} π(i)pij=π(j)pji, for all i, j
证明如下:
3. 构造状态转移概率矩阵 P P P
我们实际应用中的场景是这样的:已知目标分布 π \pi π,完成按照目标分布的采样。所以我们的目的是构造出这个目标分布对应的状态转移概率矩阵 P P P,这样我们就可以从一个初始状态不断使用MCMC进行采样了。
我们能够利用的工具就是上面介绍的细致平稳条件。
我们任取一个状态转移矩阵 Q Q Q,一般这个任取的 Q Q Q是步满足细致平稳条件的:
p ( i ) q ( i , j ) ≠ p ( j ) q ( j , i ) p(i)q(i,j) \neq p(j)q(j,i) p(i)q(i,j)=p(j)q(j,i)
我们可以构造一个 α \alpha α使上式满足细致平稳条件:
p ( i ) q ( i , j ) α ( i , j ) = p ( j ) q ( j , i ) α ( j , i ) p(i)q(i,j)\alpha(i,j) = p(j)q(j,i)\alpha(j,i) p(i)q(i,j)α(i,j)=p(j)q(j,i)α(j,i)
其中:
α ( i , j ) = p ( j ) q ( j , i ) , α ( j , i ) = p ( i ) q ( i , j ) \alpha(i,j)=p(j)q(j,i), \alpha(j,i)=p(i)q(i,j) α(i,j)=p(j)q(j,i),α(j,i)=p(i)q(i,j)
这样我们就构造出了目标马尔科夫状态转移矩阵,其中每一项都满足:
P ( i , j ) = Q ( i , j ) α ( i , j ) P(i,j)=Q(i,j)\alpha(i,j) P(i,j)=Q(i,j)α(i,j)
继承“接受-拒绝采样”和“重要性采样”中的说法,我们可以把 Q Q Q称作提议马尔科夫链,其中状态 i i i转移到状态 j j j的概率是 Q ( i , j ) Q(i,j) Q(i,j);而我们的目标马尔科夫链中,从状态 i i i转移到状态 j j j的概率是 Q ( i , j ) α ( i , j ) Q(i,j)\alpha(i,j) Q(i,j)α(i,j)。
继续继承“接受-拒绝采样”中的思想,我们可以很容易的把 α ( i , j ) \alpha(i,j) α(i,j)看做接受概率或者接受率。
4. MCMC的算法步骤
紧接上一小节, α ( i , j ) \alpha(i,j) α(i,j)表示的是采样样本的接受概率,所以MCMC的核心思想就是按照提议马尔科夫链 Q Q Q进行采样,而后按照 α ( i , j ) \alpha(i,j) α(i,j)确定采样是否被接受。MCMC的主要步骤如下:
- 初始化马尔科夫链的初始状态 X 0 = x 0 X_0 = x_0 X0=x0;
- 循环执行以下步骤(3~6),迭代若干次, t = 0 , 1 , 2 , . . . t=0,1,2,... t=0,1,2,...
- 在 t t t时刻状态 X t = x t X_t=x_t Xt=xt,按照 Q Q Q进行采样,即 y ~ q ( x ∣ x t ) y~q(x|x_t) y~q(x∣xt)
- 从均匀分布中进行采样 u ~ U n i f o r m [ 0 , 1 ] u~Uniform[0,1] u~Uniform[0,1]
- 若 u < α ( x t , y ) = p ( y ) q ( x t ∣ y ) u<\alpha(x_t,y)=p(y)q(x_t|y) u<α(xt,y)=p(y)q(xt∣y) 则接受该采样,状态 X t + 1 = y X_{t+1} = y Xt+1=y;否则不接受转移 X t + 1 = x t X_{t+1} = x_t Xt+1=xt
5. Metropolis-Hastings采样方法
M-H采样方法是对MCMC方法的一点改进,改进之后采样的接受度升高,加快了采样效率。
从第3小结中我们知道
α ( i , j ) = p ( j ) q ( j , i ) \alpha(i,j)=p(j)q(j,i) α(i,j)=p(j)q(j,i)
所以通常 α ( i , j ) \alpha(i,j) α(i,j)是一个很小的值,因此在一次采样中很容易被拒绝,从而导致采样的时间成本、计算成本很高。M-H(Metropolis-Hastings)采样,通过放大接受率 α ( i , j ) \alpha(i,j) α(i,j)提高了跳转概率,缩短了采样过程,推导过程如下:
p ( i ) q ( i , j ) p ( j ) q ( j , i ) = p ( j ) q ( j , i ) p ( i ) q ( i , j ) p ( i ) q ( i , j ) p ( j ) q ( j , i ) p ( i ) q ( i , j ) = p ( j ) q ( j , i ) \begin{aligned} p(i)q(i,j)p(j)q(j,i) &= p(j)q(j,i)p(i)q(i,j) \\ p(i)q(i,j) \frac{p(j)q(j,i)}{p(i)q(i,j)} &= p(j)q(j,i) \end{aligned} p(i)q(i,j)p(j)q(j,i)p(i)q(i,j)p(i)q(i,j)p(j)q(j,i)=p(j)q(j,i)p(i)q(i,j)=p(j)q(j,i)
有:
α ( i , j ) = p ( j ) q ( j , i ) p ( i ) q ( i , j ) , α ( j , i ) = 1 \alpha(i,j)=\frac{p(j)q(j,i)}{p(i)q(i,j)}, \alpha(j,i)=1 α(i,j)=p(i)q(i,j)p(j)q(j,i),α(j,i)=1
从公式中我们可以看出,这样计算的 α ( i , j ) \alpha(i,j) α(i,j)是可能大于1的,所以我们定义:
α ( i , j ) = m i n ( p ( j ) q ( j , i ) p ( i ) q ( i , j ) , 1 ) \alpha(i,j)=min(\frac{p(j)q(j,i)}{p(i)q(i,j)},1) α(i,j)=min(p(i)q(i,j)p(j)q(j,i),1)
这样我们就将接受概率放大了 1 p ( i ) q ( i , j ) \frac{1}{p(i)q(i,j)} p(i)q(i,j)1倍,最多可以实现满概率跳转。
最后推荐几篇相关文章:
蒙特卡洛方法:https://blog.csdn.net/bitcarmanlee/article/details/82716641
接受拒绝采样:https://www.zhihu.com/question/38056285/answer/1803920100
重要性采样:https://mathpretty.com/12375.html
马尔科夫链的平稳分布:http://www.360doc.com/content/20/0313/14/10724725_898892977.shtml
细致平稳条件、Metropolis-Hastings采样方法:https://www.zhihu.com/question/63305712/answer/1804780073
MCMC方法:https://blog.csdn.net/arcers/article/details/88732639