【LeetCode】4. 寻找两个正序数组的中位数
题目链接
文章目录
-
- Python3
-
- 方法一: 二分查找 ⟮ O ( log ( m + n ) ) 、 O ( 1 ) ⟯ \lgroup O(\log(m+n))、 O(1)\rgroup ⟮O(log(m+n))、O(1)⟯
- ⭐ 方法二: 划分数组 ⟮ O ( log ( min ( m , n ) ) 、 O ( 1 ) ⟯ \lgroup O(\log( \min(m, n))、 O(1)\rgroup ⟮O(log(min(m,n))、O(1)⟯
- 方法: 额外数组归并,直接定位中位数 ⟮ O ( m + n ) ⟯ \lgroup O(m+n)\rgroup ⟮O(m+n)⟯
- C++
-
- 方法一: 二分查找 ⟮ O ( log ( m + n ) ) 、 O ( 1 ) ⟯ \lgroup O(\log(m+n))、 O(1)\rgroup ⟮O(log(m+n))、O(1)⟯
- ⭐ 方法二: 划分数组 ⟮ O ( log ( min ( m , n ) ) 、 O ( 1 ) ⟯ \lgroup O(\log( \min(m, n))、 O(1)\rgroup ⟮O(log(min(m,n))、O(1)⟯
-
- 二分查找 理解

二分查找
常见复杂度排序: O ( 1 ) < O ( log n ) < O ( n ) < O ( n log n ) < O ( n 2 ) < O ( n 3 ) < O ( 2 2 ) < O ( n ! ) < O ( n n ) O(1) < O(\log n) < O(n) < O(n\log n) < O(n^2) < O(n^3) < O(2^2) < O(n!) < O(n^n) O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(22)<O(n!)<O(nn)

中位数 定义: 将一个集合划分为两个长度相等的子集,其中一个子集中的元素总是大于另一个子集中的元素。
k = (len(nums1)+len(nums2)+1)//2
奇数: 实际中位数为 k-1
偶数: 实际中位数为 k, k-1 两者的均值
Python3
方法一: 二分查找 ⟮ O ( log ( m + n ) ) 、 O ( 1 ) ⟯ \lgroup O(\log(m+n))、 O(1)\rgroup ⟮O(log(m+n))、O(1)⟯
页面内跳转: 查看补充内容增强理解
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
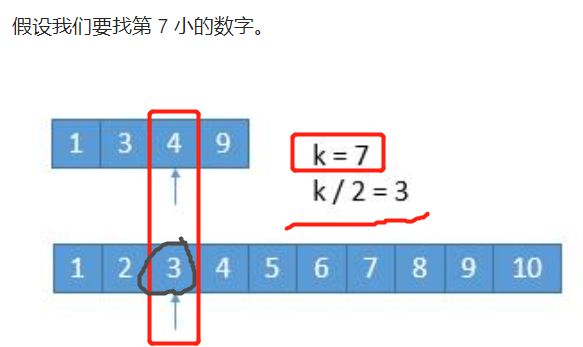
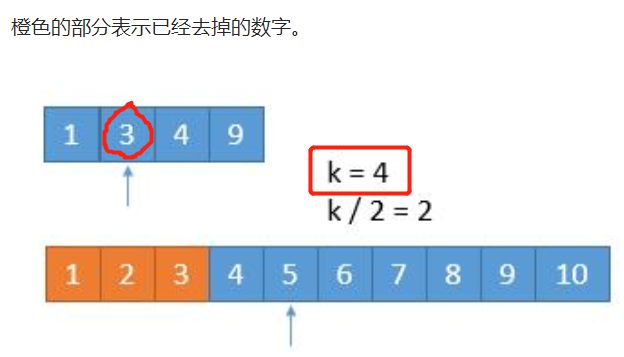
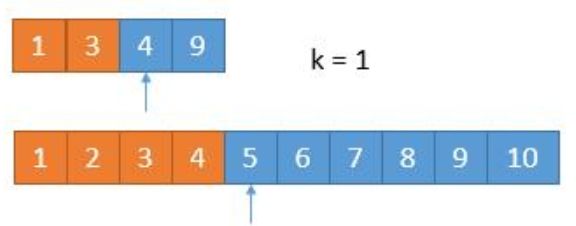
# 子模块: 查找 第 k 小 的数
def getKthElement(k):
index1, index2 = 0, 0 # 剩余元素 的起始下标
while True:
# 递归 跳出 条件
if index1 == m: # nums1 的元素 已被全部去掉 注意 nums1最后一个元素的下标是 m-1
return nums2[index2 + k - 1] # 直接在 nums2剩余元素中 返回 第 k 小 的数
if index2 == n: #
return nums1[index1 + k - 1]
if k == 1: ## 在剩下的元素里 返回 第 1 小的元素
return min(nums1[index1], nums2[index2])
# 一般情况
newIndex1 = min(index1 + k // 2 - 1, m-1) # 要是 newIndex1 == m, 就要跳出了
newIndex2 = min(index2 + k // 2 - 1, n-1)
pivot1, pivot2 = nums1[newIndex1], nums2[newIndex2]
if pivot1 <= pivot2:
k -= newIndex1 - index1 + 1 # 更新 k
index1 = newIndex1 + 1
else:
k -= newIndex2 - index2 + 1
index2 = newIndex2 + 1
m, n = len(nums1), len(nums2)
totalLength = m + n
if totalLength % 2 == 1: # 奇数
return getKthElement((totalLength + 1) // 2)
else: # 偶数
return (getKthElement(totalLength // 2) + getKthElement(totalLength // 2 + 1)) /2
⭐ 方法二: 划分数组 ⟮ O ( log ( min ( m , n ) ) 、 O ( 1 ) ⟯ \lgroup O(\log( \min(m, n))、 O(1)\rgroup ⟮O(log(min(m,n))、O(1)⟯
中位数的作用: 将一个集合划分为两个长度相等的子集,其中一个子集中的元素总是大于另一个子集中的元素。
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
if len(nums1) > len(nums2): # 保证 nums1 是较短的
return self.findMedianSortedArrays(nums2,nums1)
m, n = len(nums1), len(nums2)
left, right = 0, m # 两个 数组 在 合并数组的 填充起始下标
median1 = 0 # 前一部分的 最大值
median2 = 0 # 后一部分的 最小值
while left <= right:
i = (left + right) // 2
j = (m + n + 1) // 2 - i
# 前一部分包含 nums1的前面部分 和 nums2 的前面部分
# 后一部分 包含 nums1 的后面部分 + nums2 的后面部分
# 维护 分界线 附近 的四个数
nums_im1 = (-math.inf if i == 0 else nums1[i-1]) # i minus 1 nums1 前半部分 最大值
nums_i = (math.inf if i == m else nums1[i]) # nums1 后半部分 最小值
nums_jm1 = (-math.inf if j == 0 else nums2[j-1]) # nums2 前半部分 最大值
nums_j = (math.inf if j == n else nums2[j]) # nums2 后半部分 最小值
if nums_im1 <= nums_j:
median1, median2 = max(nums_im1, nums_jm1), min(nums_i,nums_j)
left = i + 1
else:
right = i - 1
return (median1 + median2) / 2 if (m + n) % 2 == 0 else median1
方法: 额外数组归并,直接定位中位数 ⟮ O ( m + n ) ⟯ \lgroup O(m+n)\rgroup ⟮O(m+n)⟯
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
"""额外数组"""
nums = []
i, j = 0, 0
while i < len(nums1) and j < len(nums2):
if nums1[i] <= nums2[j]:
nums.append(nums1[i])
i += 1
else:
nums.append(nums2[j])
j += 1
if i < len(nums1):
nums.extend(nums1[i:])
if j < len(nums2):
nums.extend(nums2[j:])
n = len(nums)
if n % 2 == 0: ### 偶数个
m = n // 2 ## 10//2 = 5 中间下标4, 5
return (nums[m-1] + nums[m])/2
else:
return nums[n//2]
C++
方法一: 二分查找 ⟮ O ( log ( m + n ) ) 、 O ( 1 ) ⟯ \lgroup O(\log(m+n))、 O(1)\rgroup ⟮O(log(m+n))、O(1)⟯
class Solution {
public:
// 子模块
int getKthElement(vector<int>& nums1, vector<int>& nums2, int k){
int index1 = 0, index2 = 0;
int m = nums1.size(), n = nums2.size();
while (true){
// 跳出条件
if (index1 == m){
return nums2[index2 + k - 1];
}
if (index2 == n){
return nums1[index1 + k -1];
}
if (k == 1){
return min(nums1[index1], nums2[index2]);
}
// 一般情况
int newIndex1 = min(index1 + k / 2 - 1, m - 1);
int newIndex2 = min(index2 + k / 2 - 1, n - 1);
int pivot1 = nums1[newIndex1];
int pivot2 = nums2[newIndex2];
if (pivot1 < pivot2){
k -= newIndex1 - index1 + 1;
index1 = newIndex1 + 1;
}
else{
k -= newIndex2 - index2 + 1;
index2 = newIndex2 + 1;
}
}
}
// 主模块
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size(), n = nums2.size();
int TotalLength = m + n;
if (TotalLength % 2 == 1){// 奇数
return getKthElement(nums1, nums2, (TotalLength + 1)/2); // 注意 写法
}
else{ // 偶数
return (getKthElement(nums1, nums2, TotalLength / 2) + getKthElement(nums1, nums2, TotalLength / 2 + 1))/2.0;
}
}
};
⭐ 方法二: 划分数组 ⟮ O ( log ( min ( m , n ) ) 、 O ( 1 ) ⟯ \lgroup O(\log( \min(m, n))、 O(1)\rgroup ⟮O(log(min(m,n))、O(1)⟯
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
if (nums1.size() > nums2.size()){
return findMedianSortedArrays(nums2, nums1);
}
int m = nums1.size(), n = nums2.size();
int left = 0, right = m;
int median1 = 0, median2 = 0; // 前一部分的 最大值 后一部分的最小值
while (left <= right){
int i = (left + right) / 2; // nums1 分界
int j = (m + n + 1)/2 - i; // nums2 分界
// 维护 分界线 附近的 四个数
int nums_im1 = (i == 0 ? INT_MIN : nums1[i-1]);
int nums_i = (i == m ? INT_MAX : nums1[i]) ; // nums1 右侧的最小值
int nums_jm1 = (j == 0 ? INT_MIN : nums2[j-1]);
int nums_j =(j == n ? INT_MAX : nums2[j]);
if (nums_im1 <= nums_j){// 最大值 小于 最小值
median1 = max(nums_im1, nums_jm1);
median2 = min(nums_i, nums_j);
left = i + 1;
}
else{
right = i - 1;
}
}
return (m + n) % 2 == 0 ? (median1 +median2) / 2.0 : median1;
}
};
二分查找 理解
返回之前的地方