【小呆的概率论学习笔记】抽样调查之用抽样样本估计母体数字特征

1. 随机变量的数字特征

随机变量本质上是一个随机数，他以概率的形式取任何可能的取值，但是随机变量取值却有一定的规律，我们可以称之为随机变量的数字特征。最简明、最常用的随机变量的数字特征就是均值（或者说期望）和方差。

1.1 随机变量的均值（期望）

随机变量的均值的意义类似于概率平均，意味着随机变量的取值大概率围绕这个均值并在一定的范围内变化。如下图所示。

那么概率平均的计算就可以参照加权平均的形式给定出。假设n个数$x_1、x_2、\dots \dots 、x_n$的权分别是$w_1、w_2、\dots \dots 、w_n$，难么加权平均值为
$$\overline{x}=\frac{x_1{w}_1+x_2{w}_2+\dots \dots +x_n{w}_n}{n}$$
上式为加权平均公式，那么类似的，概率平均可以把随机变量的各个取值的概率当成每个取值的$\frac{权数}{总数}$，显然这样的概率平均，也就是均值（期望）可以表示成
$$E(X)=\sum _{i=1}^n{x}_{i}p(x_i)$$
其中$p(x_i)$是$X=x_i$的概率。
当然如果随机变量X是连续随机变量，那么均值的公式等效的变化成
$$E(X)={\int }_{-\infty }^{\infty }{x}_{i}dp(x_i)={\int }_{-\infty }^{\infty }{x}_{i}f(x_i)d{x}_i={\int }_{-\infty }^{\infty }xf(x)dx$$

1.2 随机变量的方差

前面对随机变量的均值或者说期望进行了讨论，总的来说随机变量每次取值都会在均值的一定范围内变化，就是说会有几次取值比均值大，当然也会 有几次取值比均值小。这对于我们评估和使用非常重要。均值最典型应用是在于投资，当投资期望=成功率×收益+失败率×损失>0，那么这笔投资总是一笔不差的投资（理论计算）。
此外，这个随机变量围绕均值偏离的程度也是一个重要的衡量，有时候对于实际使用中有很大的影响。在很多情况，人们可能更喜欢偏离程度有限的选择，典型的比如人们喜欢波动小的股票，工厂往往控制质量，使得产品一致性尽可能高。
下图为同均值情况下不同方差的数据集，左图为小方差，右图为大方差。

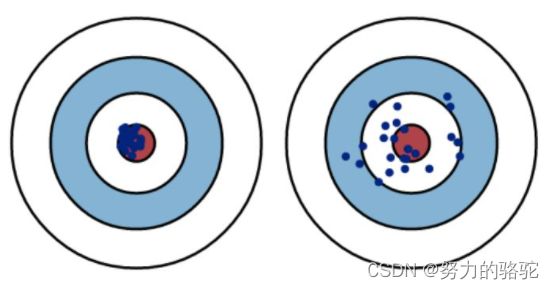
那么，就引出来用随机变量偏离均值的程度来定义方差，以便用方差来衡量这种离散程度，即

$$D(X)=E\{[X-E(X){]}^2\}$$
那么，离散随机变量的方差表达式如下
$$D(X)=E\{[X-E(X){]}^2\}=\sum (x_i-\mu {)}^{2}p(x_i)$$
连续随机变量的方差表达式如下
$$\begin{array}{rl}D(X)& =E\{[X-E(X){]}^2\}\\ & ={\int }_{-\infty }^{\infty }(x_i-\mu {)}^{2}dp(x_i)\\ & ={\int }_{-\infty }^{\infty }(x_i-\mu {)}^{2}f(x_i)d{x}_i\\ & ={\int }_{-\infty }^{\infty }(x-\mu {)}^{2}f(x)dx\end{array}$$

1.3 随机变量的协方差

随机变量的方差能够度量其变异性，那么如果随机变量超过一个，就需要考虑怎么度量随机变量联合变异性或者说度量随机变量的关联度。参考方差的定义，我们可以定义协方差来定义这种度量
$$\mathbf{Cov}(x_i,x_j)=E[(x_i-{\mu }_{x_i})(x_j-{\mu }_{x_j})]$$
那么，协方差有以下特性
a) i=j时，协方差就等于方差，即方差是协方差的一种特殊情况
$$\mathbf{Cov}(x_i,x_i)=E[(x_i-{\mu }_{x_i})(x_i-{\mu }_{x_i})]={\sigma }^2$$
b) 如果x_i与x_j相互独立，那么就没有联合变异性或者关联度，协方差也能够反映这种情况，如下
$$\begin{array}{rl}\mathbf{Cov}(x_i,x_j)& =E[(x_i-{\mu }_{x_i})(x_j-{\mu }_{x_j})]\\ & =E(x_i{x}_j-{\mu }_{x_i}{x}_j-x_i{\mu }_{x_j}+{\mu }_{x_i}{\mu }_{x_j})\\ & =E(x_i{x}_j)-{\mu }_{x_i}E(x_j)-E(x_i){\mu }_{x_j}+{\mu }_{x_i}{\mu }_{x_j}\\ & =E(x_i{x}_j)-{\mu }_{x_i}{\mu }_{x_j}-{\mu }_{x_i}{\mu }_{x_j}+{\mu }_{x_i}{\mu }_{x_j}\\ & =E(x_i{x}_j)-{\mu }_{x_i}{\mu }_{x_j}\end{array}$$
如果x_i与x_j相互独立，就有$E(x_i{x}_j)=E(x_i)E(x_j)={\mu }_{x_i}{\mu }_{x_j}$，那么

$$\mathbf{Cov}(x_i,x_j)=E(x_i{x}_j)-{\mu }_{x_i}{\mu }_{x_j}=0$$

2. 抽样调查

自然界有些随机变量的总体或者母体${}^{[注1]}$是有限的，比如从一副扑克牌中抽一张，他的总体也就是只有108种可能，一次美国大选，支持拜登或者支持特朗普的票数总是有限的可能，有一些随机变量的总体却是无限的，比如像连续型随机变量。

注1：随机变量所有可能的取值组成的全体，称为样本空间或者总体或者母体。

那么，实际生活或者工作中，我们总需要通过观察或者少数试验来评价或者估计事务的某种可能性，诶，我们往往就通过抽样调查来实现。

当然，其实抽样调查组成的抽样样本也是随机的，比如在拜登和川普的美国大选中，我们抽取100个人做调查，其中有53个人支持拜登，47个人支持川普，但是我们如果再抽100人，可能48个人支持拜登，52个人支持川普，由此不难看出抽样样本本身也是随机的，那么抽样样本的数字特征也是一个随机变量，用它来评估母体样本的数字特征，我们需要研究其是否具备的代表性或者有效性。

在抽样调查中，有两种类型，一是重复抽样，即抽样调查的每一个样本是相互独立的，二是无重复抽样，即抽样调查的每一个样本是不是相互独立的。

3. 用抽样样本估计母体数字特征

3.1 估计母体样本均值

假设母体样本为$\Omega =\{x_1,x_2,\dots \dots ，x_n\}$，而抽样样本为$\omega =\{{\hat{x}}_1,{\hat{x}}_2,\dots \dots ,{\hat{x}}_m\}$，母体样本的均值为
$$\mu =\sum _{i=1}^n{x}_{i}p(x_i)=\frac{1}{n}\sum _{i=1}^n{x}_i$$
当然这里${\hat{x}}_i$也是$\Omega$内的 元素。
那么我们寻求利用抽样数据来找到一个能够相对准确可靠的估计母体样本均值的公式。其实，很容易想到用抽样数据的均值来估计母体样本的均值，那么这样是否是足够可靠的。因为抽样数据的均值其实也是一个随机数，那么相对准确可靠的含义我想应该是抽样样本均值这个随机变量应该是围绕真实值（母体均值）在一定范围内变化，也就是说抽样样本的均值的期望应该是等于母体均值。

如果抽样样本的均值
$$\overline{x}=\sum _{i=1}^m{\hat{x}}_{i}p({\hat{x}}_i)=\frac{1}{m}\sum _{i=1}^m{\hat{x}}_i$$
注意此时$\overline{x}$也是随机变量。

那么上文翻译成数学语言应该就是
$$E(\overline{x})=\mu$$
实际上
$$\begin{array}{rl}E(\overline{x})& =E\{\frac{1}{m}\sum _m{\hat{x}}_i\}\\ & =\frac{1}{m}\sum _{m}E({\hat{x}}_i)=\frac{1}{m}\cdot \sum _m\mu =\mu \end{array}$$
因此抽样样本均值的期望应该是等于母体样本的均值，像这种估计我们称为无偏估计（即不存在系统性偏差的估计）,如下图所示。上图是无偏估计，下图是有偏估计。

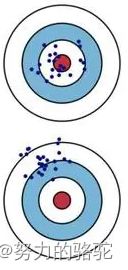
用抽样样本均值估计母体均值是一种无偏估计。
当然，不管如何，一定要记住$\overline{x}$是随机变量，即在任何一次调查中得到的样本均值都不会等于母体样本的均值。

3.2 抽样样本均值的方差

既然抽样样本均值$\overline{x}$是随机变量，那么也可以通过其方差来评价$\overline{x}$的离散程度。按照方差的定义，有
$$\begin{array}{rl}D(\overline{x})& =E\{[\overline{x}-E(\overline{x}){]}^2\}\\ & =E\{[\frac{1}{m}\sum _{i=1}^m{\hat{x}}_i-\mu {]}^2\}\\ & =E\{\frac{1}{m}[\sum _{i=1}^m{\hat{x}}_i-m\mu ]\cdot \frac{1}{m}[\sum _{i=1}^m{\hat{x}}_i-m\mu ]\}\\ & =\frac{1}{m^2}E\{[\sum _{i=1}^m({\hat{x}}_i-\mu )]\cdot [\sum _{i=1}^m({\hat{x}}_i-\mu )]\}\\ & =\frac{1}{m^2}E\{\sum _{i=1}^m\sum _{j=1}^m({\hat{x}}_i-\mu )({\hat{x}}_j-\mu )\}\\ & =\frac{1}{m^2}\sum _{i=1}^m\sum _{j=1}^{m}E\{({\hat{x}}_i-\mu )({\hat{x}}_j-\mu )\}\\ & =\frac{1}{m^2}\sum _{i=1}^m\sum _{j=1}^m\mathbf{Cov}({\hat{x}}_i,{\hat{x}}_j)\\ & =\frac{1}{m^2}\sum _{i=1}^m\mathbf{Cov}({\hat{x}}_i,{\hat{x}}_i)+\frac{1}{m^2}\sum _{i=1}^m\sum _{j\ne i}^m\mathbf{Cov}({\hat{x}}_i,{\hat{x}}_j)\end{array}$$
其中，如果${\hat{x}}_i$是独立的，那么$\mathbf{Cov}({\hat{x}}_i,{\hat{x}}_j)\stackrel{i\ne j}{}0$，$\mathbf{Cov}({\hat{x}}_i,{\hat{x}}_j)\stackrel{i=j}{}\mathbf{Cov}({\hat{x}}_i,{\hat{x}}_i)=D({\hat{x}}_i)={\sigma }^2$。

$$D(\overline{x})=\frac{1}{m^2}\sum _{i=1}^m\mathbf{Cov}({\hat{x}}_i,{\hat{x}}_i)=\frac{1}{m^2}\cdot m{\sigma }^2=\frac{{\sigma }^2}{m}$$

如果抽样是不重复的，那么${\hat{x}}_i$就不是独立。以离散随机变量为例，假设母体样本总共有N个元素，那么
$$\begin{array}{rl}\mathbf{Cov}({\hat{x}}_i,{\hat{x}}_j)& =E({\hat{x}}_i{\hat{x}}_j)-E({\hat{x}}_i)E({\hat{x}}_j)\\ & =\sum _{k=1}^m\sum _{l=1}^m{\hat{\eta }}_k{\hat{\eta }}_{l}P({\hat{x}}_i={\hat{\eta }}_k并{\hat{x}}_j={\hat{\eta }}_l)\\ & =\sum _{k=1}^m{\hat{\eta }}_{k}P({\hat{x}}_i={\hat{\eta }}_k)\sum _{l=1}^m{\hat{\eta }}_{l}P({\hat{x}}_j={\hat{\eta }}_l|{\hat{x}}_i={\hat{\eta }}_k)\end{array}$$
条件概率$P({\hat{x}}_j={\hat{\eta }}_l|{\hat{x}}_i={\hat{\eta }}_k)$由下式确定

$$P({\hat{x}}_j={\hat{\eta }}_l|{\hat{x}}_i={\hat{\eta }}_k)=\{\begin{array}{l}\frac{n_l}{N-1},l\ne k\\ \frac{n_l-1}{N-1},l=k\end{array}$$
其中$n_l$是母体样本中${\eta }_l$的个数，N-1是${\hat{x}}_i={\eta }_k$抽样后的母体样本数（因为是不重复抽样，所以母体样本变少了），如果$l=k$那么相应的${\eta }_l$的个数也要减一。
$$\begin{array}{rl}\mathbf{Cov}({\hat{x}}_i,{\hat{x}}_j)& =E({\hat{x}}_i{\hat{x}}_j)-E({\hat{x}}_i)E({\hat{x}}_j)\\ & =\sum _{k=1}^m{\hat{\eta }}_{k}P({\hat{x}}_i={\hat{\eta }}_k)\sum _{l=1}^m{\hat{\eta }}_{l}P({\hat{x}}_j={\hat{\eta }}_l|{\hat{x}}_i={\hat{\eta }}_k)-{\mu }^2\\ & =\sum _{k=1}^m{\hat{\eta }}_k\frac{n_k}{N}(\sum _{l=1,l\ne k}^m{\hat{\eta }}_l\frac{n_l}{N-1}+{\hat{\eta }}_k\frac{n_k-1}{N-1})-{\mu }^2\\ & =\sum _{k=1}^m{\hat{\eta }}_k\frac{n_k}{N}(\sum _{l=1,l\ne k}^m{\hat{\eta }}_l\frac{n_l}{N-1}+{\hat{\eta }}_k\frac{n_k}{N-1}-{\hat{\eta }}_k\frac{1}{N-1})-{\mu }^2\\ & =\sum _{k=1}^m{\hat{\eta }}_k\frac{n_k}{N}(\sum _{l=1}^m{\hat{\eta }}_l\frac{n_l}{N-1}-{\hat{\eta }}_k\frac{1}{N-1})-{\mu }^2\\ & =\sum _{k=1}^m{\hat{\eta }}_k\frac{n_k}{N}\sum _{l=1}^m{\hat{\eta }}_l\frac{n_l}{N-1}-\sum _{k=1}^m{\hat{\eta }}_k^2\frac{n_k}{N(N-1)}-{\mu }^2\\ & =\frac{1}{N(N-1)}(\sum _{k=1}^m{\hat{\eta }}_k{n}_k\sum _{l=1}^m{\hat{\eta }}_l{n}_l-\sum _{k=1}^m{\hat{\eta }}_k^2{n}_k)-{\mu }^2\\ & =\frac{1}{N(N-1)}[(\sum _{i=1}^N{x}_i{)}^2-\sum _{i=1}^N{\hat{x}}_i^2]-{\mu }^2\\ & =\frac{1}{N(N-1)}(N^2{\mu }^2-N{\mu }^2-N{\sigma }^2)-{\mu }^2\\ & =-\frac{1}{N-1}{\sigma }^2\end{array}$$
上式过程中需要用到几个关系式：
a) 期望定义式
$$\begin{gathered} E({\hat{x}}_i)=\sum _{i=1}^N{\hat{x}}_{i}p({\hat{x}}_i)=\sum _{i=1}^N{\hat{x}}_i\frac{1}{N}=\frac{1}{N}\sum _{i=1}^N{\hat{x}}_i \\ =\sum _{j=1}^m{\hat{x}}_j\frac{n_j}{N} \end{gathered}$$
那么相应的
$$E({\hat{x}}_i^2)=\frac{1}{N}\sum _{i=1}^N{\hat{x}}_i^2=\frac{1}{N}\sum _{j=1}^m{\hat{x}}_j{n}_j$$
同时，有
$$E({\hat{x}}_i)=\frac{1}{N}\sum _{i=1}^N{\hat{x}}_i=\mu$$
可以推得
$$\sum _{i=1}^N{\hat{x}}_i=N\mu$$
b) 期望与方差的关系式
这里需要引用方差和期望的一些关系 。
$$\begin{array}{rl}D({\hat{x}}_i)& =E\{[{\hat{x}}_i-E({\hat{x}}_i){]}^2\}\\ & =E\{{\hat{x}}_i^2-2{\hat{x}}_i\mu +{\mu }^2\}\\ & =E({\hat{x}}_i^2)-2\mu \cdot E({\hat{x}}_i)+{\mu }^2\\ & =E({\hat{x}}_i^2)-{\mu }^2={\sigma }^2\end{array}$$
同时，应用a)，有
$$E({\hat{x}}_i^2)={\mu }^2+{\sigma }^2=[E({\hat{x}}_i){]}^2+D({\hat{x}}_i)=\frac{1}{N}\sum _{i=1}^N{\hat{x}}_i^2$$
那么
$$\sum _{i=1}^N{\hat{x}}_i^2=N{\mu }^2+N{\sigma }^2$$

应用上述公式，那么均值方差如下式
$$\begin{array}{rl}D(\overline{x})& =\frac{1}{m^2}\sum _{i=1}^m\mathbf{Cov}({\hat{x}}_i,{\hat{x}}_i)+\frac{1}{m^2}\sum _{i=1}^m\sum _{j\ne i}^m\mathbf{Cov}({\hat{x}}_i,{\hat{x}}_j)\\ & =\frac{1}{m^2}m{\sigma }^2-\frac{1}{m^2}\sum _{i=1}^m\sum _{j\ne i}^m\frac{1}{N-1}{\sigma }^2\\ & =\frac{1}{m}{\sigma }^2-\frac{1}{m^2}m(m-1)\frac{1}{N-1}{\sigma }^2\\ & =\frac{1}{m}{\sigma }^2(1-\frac{m-1}{N-1})\end{array}$$
从上式可以看到$(1-\frac{m-1}{N-1})$就是重复抽样和非重复抽样的区别，当母体样本非常非常大时，该式趋于1，这也是可以理解的，我们从大样本中抽除一个数，几乎不影响其概率特性。

3.2 估计母体样本方差

方差是一个重要的参数，因此通过抽样调查得到的样本数据来估计母体样本的方差将是一项重要的任务。回顾母体方差是随机变量与母体样本均值偏离的平方平均，所以很自然的用同样的方式来估计，也就是用抽样样本均值的平方偏离的平均来估计：
$${\hat{\sigma }}^2=\frac{1}{m}\sum _{i=1}^m({\hat{x}}_i-\overline{x}{)}^2$$
那么，用抽样样本的数据计算的${\hat{\sigma }}^2$，我们用它来评估母体样本的数字特征，是否具备的代表性或者有效性。也就是说有没有产生系统性偏差，即是否是无偏估计，如果是无偏估计，那么有$E({\hat{\sigma }}^2)={\sigma }^2$，否则，$E({\hat{\sigma }}^2)\ne {\sigma }^2$。

$$\begin{array}{rl}E({\hat{\sigma }}^2)& =E\{\frac{1}{m}\sum _{i=1}^m({\hat{x}}_i-\overline{x}{)}^2\}\\ & =E\{\frac{1}{m}\sum _{i=1}^m{\hat{x}}_i^2-\frac{1}{m}\sum _{i=1}^{m}2\cdot {\hat{x}}_i\overline{x}+\frac{1}{m}\sum _{i=1}^m{\overline{x}}^2\}\\ & =E\{\frac{1}{m}\sum _{i=1}^m{\hat{x}}_i^2\}-E\{2\overline{x}\cdot \frac{1}{m}\sum _{i=1}^m{\hat{x}}_i\}+E\{\frac{1}{m}\sum _{i=1}^m{\overline{x}}^2\}\\ & =\frac{1}{m}\sum _{i=1}^{m}E({\hat{x}}_i^2)-E(2\overline{x}\cdot \overline{x})+E(\frac{1}{m}\cdot m{\overline{x}}^2)\\ & =\frac{1}{m}\sum _{i=1}^{m}E({\hat{x}}_i^2)-E({\overline{x}}^2)\end{array}$$

同时
$$E({\hat{x}}_i^2)=[E({\hat{x}}_i){]}^2+D({\hat{x}}_i)={\mu }^2+{\sigma }^2$$

$$E({\overline{x}}_i^2)=[E({\overline{x}}_i){]}^2+D({\overline{x}}_i)$$

$E({\overline{x}}_i^2)$分两种情况，重复抽样或者非重复抽样，那么如果是重复抽样，则
a) 重复抽样
$$E({\overline{x}}_i^2)=[E({\overline{x}}_i){]}^2+D({\overline{x}}_i)={\mu }^2+\frac{{\sigma }^2}{m}$$

$$\begin{array}{rl}E({\hat{\sigma }}^2)& =\frac{1}{m}\sum _{i=1}^{m}E({\hat{x}}_i^2)-E({\overline{x}}^2)\\ & =\frac{1}{m}\sum _{i=1}^m({\mu }^2+{\sigma }^2)-({\mu }^2+\frac{{\sigma }^2}{m})\\ & =({\mu }^2+{\sigma }^2)-({\mu }^2+\frac{{\sigma }^2}{m})\\ & =\frac{m-1}{m}{\sigma }^2\ne {\sigma }^2\end{array}$$
因此，用${\hat{\sigma }}^2$来估计${\sigma }^2$，有系统性偏差，即是有偏估计。当然也不难推得，$\frac{m}{m-1}{\hat{\sigma }}^2=\frac{1}{m-1}{\sum }_{i=1}^m({\hat{x}}_i-\overline{x}{)}^2$是${\sigma }^2$的无偏估计。
如果是非重复抽样，则
b) 非重复抽样
$$E({\overline{x}}_i^2)=[E({\overline{x}}_i){]}^2+D({\overline{x}}_i)={\mu }^2+\frac{{\sigma }^2}{m}(1-\frac{m-1}{N-1})$$

$$\begin{array}{rl}E({\hat{\sigma }}^2)& =\frac{1}{m}\sum _{i=1}^{m}E({\hat{x}}_i^2)-E({\overline{x}}^2)\\ & =\frac{1}{m}\sum _{i=1}^m({\mu }^2+{\sigma }^2)-[{\mu }^2+\frac{{\sigma }^2}{m}(1-\frac{m-1}{N-1})]\\ & =({\mu }^2+{\sigma }^2)-[{\mu }^2+\frac{{\sigma }^2}{m}(1-\frac{m-1}{N-1})]\\ & =\frac{m-1}{m}{\sigma }^2(1-\frac{m-1}{N-1})\ne {\sigma }^2\end{array}$$
同样，此时${\hat{\sigma }}^2$也是${\sigma }^2$有偏估计，当然也不难推得，$\frac{m}{m-1}\frac{N-1}{N-m}{\hat{\sigma }}^2=\frac{1}{m-1}\frac{N-1}{N-m}{\sum }_{i=1}^m({\hat{x}}_i-\overline{x}{)}^2$是${\sigma }^2$的无偏估计。