机器学习笔记(三)
神经网络训练中的问题(二)
Batch and Momentum
Batch之前有说过,实际上在算微分的时候,并不是真的对所有 Data 算出来的 L 作微分,你是把所有的 Data 分成一个一个的 Batch,每次在更新参数时实际上是对每一个batch进行操作,所有的batch看过一遍叫做一个 Epoch。
那么就存在这样一个问题,batch的大小如何选择?
取两个极端的情况,同样是一个20个数据大小数据集,第一次我们将batch的大小定位20,也叫Full batch,第二次我们将batch的大小定位1,总共进行20此update。蓝色线代表着数据更新的方向。从图中可知:
左边的步数很少,但每一步运算的时间很长,右边每步运算时间很短,但方向比较嘈杂(Noisy)。但实际计算过程中,由于GPU存在着并行计算,少量的增加Btch size并不会引起时间上特别大的变化,在当今的计算环境下,在做 MNIST 做手写数字辨识时,1batch size和1000batch size的计算时间几乎一致,这就导致了在一定程度上增加batch size不仅不会将每步的计算时间增多,反而会大幅度减少一轮Epoch所需要的时间。
那么Batch的大小对Loss有什么影响呢?
这是另外一篇论文给出的答案,从Validation ACC(正确率)的结果上看Batch Size 越大,Validation Acc 上的结果越差。
这是一种常规的解释: 假设你是 Full Batch,那你今天在 Update 你的参数的时候,你就是沿著一个 Loss Function 来 Update 参数,今天 Update 参数的时候走到一个 Local Minima,走到一个 Saddle Point,显然就停下来了,Gradient 是零,如果你不特别去看Hession的话,那你用 Gradient Descent 的方法,你就没有办法再更新你的参数了。但是假如是 Small Batch 的话,因為我们每次是挑一个 Batch 出来算它的 Loss,你每一次 Update 你的参数的时候,你用的 Loss Function 都是越有差异的,你选到第一个 Batch 的时候,你是用 L1 来算你的 Gradient,你选到第二个 Batch 的时候,你是用 L2 来算你的 Gradient,假设你用 L1 算 Gradient 的时候,发现 Gradient 是零卡住了,但 L2 它的 Function 跟 L1 又不一样,L2 就不一定会卡住,所以 L1 卡住了没关系,换下一个 Batch 来,L2 再算Gradient。
那么Batch的大小对 Testing有什么影响呢?
根据实验小的 Batch,居然在 Testing 的时候会是比较好的。
一般是这么解释的:在这个 Training Loss 上面呢,可能有很多个 Local Minima,有不只一个 Local Minima,那这些 Local Minima 它们的 Loss 都很低,它们 Loss 可能都趋近于 0,但是这个 Local Minima还是有好 Minima 跟坏 Minima 之分。如果一个 Local Minima在平坦的地方,我们称之为好的 Local Minima,反之则为不好的 Local Minima。
那当 Training 跟 Testing的Function有着细微的差距,计算出的Loss也有着细微的差距。在好的Local Minima上差距很小,但在坏的Local Minima上差距很大。当Batch很小的时候它有很多的 Loss,它每次 Update 的方向都不太一样,所以如果今天这个Loss非常地窄,它可能一个不小心就跳出去了,它的 Update 的方向也就随机性,直到如果有一个非常宽的盆地,它才会停下来,对于大的Batch由于更新的次数少,更可能走进比较窄的Loss里面。
综上所述,Small Batch和Large Batch的优缺点总结如下:
Adaptive Learning Rate
先来看一个实验:
一个非常简单的error surface ,在纵向的变化特别密集,在横向的变化特别平滑,可以理解成上面的“等高线”是一个长轴特别长,短轴特别短的椭圆。我们现在要从黑点这个地方当作初始点,目标的最佳点是×所在的位置。
当我们把learning rate设置成 1 0 − 2 10^{-2} 10−2的时候结果如下:
可见learning rate设置的太大了,在纵向跨度太大无法有效的更新参数。逐渐降低learning rate,直至 1 0 − 7 10^{-7} 10−7的时候,终于在纵轴不在震荡了。
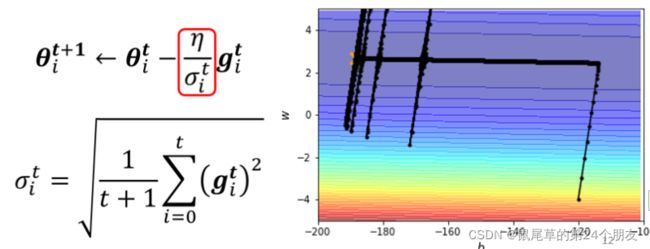
但纵向更新完向左走的时候,尽管已经更新了10w次还是没有办法向左前进很多,很显然就算一个最简单的error surface单纯的使用gradient descend也很难train。这是因为我们的learning rate永远都是一个固定的值,在应对不同的Loss的时候更新参数表现不一样。所以不同的parameter应该有不同的learning rate。这就是Adaptive Learning Rate。
我们之前更新参数的方程为: θ i t + 1 ← θ i t − η g i t {θ{_i}{^{t+1}}} ← {θ{_i}{^{t}}}-{\eta}{g{_i}{^{t}}} θit+1←θit−ηgit η \eta η的值固定不变,我们现在进行改进将此项改为 η σ ᵢ ᵗ \frac{η}{σᵢᵗ} σᵢᵗη,公式更新为: θ i t + 1 ← θ i t − η σ ᵢ ᵗ g i t {θ{_i}{^{t+1}}} ← {θ{_i}{^{t}}}-{\frac{η}{σᵢᵗ}}{g{_i}{^{t}}} θit+1←θit−σᵢᵗηgit
其 σ ᵢ 0 = ( g i 0 ) 2 = ∣ g i 0 ∣ , σ ᵢ 1 = 1 2 [ ( g i 0 ) 2 + ( g i 1 ) 2 ] {σᵢ^0}=\sqrt{({g{_i}{^{0}}})^2}=|{g{_i}{^{0}}}|,{σᵢ^1}=\sqrt{\frac{1}{2}[{(g{_i}{^{0}}})^2+{(g{_i}{^{1}}})^2]} σᵢ0=(gi0)2=∣gi0∣,σᵢ1=21[(gi0)2+(gi1)2]
σ ᵢ 2 = 1 3 [ ( g i 0 ) 2 + ( g i 1 ) 2 + ( g i 2 ) 2 ] , σ ᵢ t = 1 t + 1 ∑ i = 0 t ( g i t ) 2 {σᵢ^2}=\sqrt{\frac{1}{3}[{(g{_i}{^{0}}})^2+{(g{_i}{^{1}}})^2+{(g{_i}{^{2}}})^2]},{σᵢ^t}=\sqrt{\frac{1}{t+1}\sum_{i=0}^{t}{(g{_i}{^{t}}})^2} σᵢ2=31[(gi0)2+(gi1)2+(gi2)2],σᵢt=t+11i=0∑t(git)2
这样做有什么好处呢,可以看到在 η \eta η固定的时候,如果这个loss的坡度较陡峭,也就意味着之前的 g g g的和比较大, σ σ σ的值就比较大, η σ ᵢ ᵗ \frac{η}{σᵢᵗ} σᵢᵗη的值就比较小,此时learning rate就比较小。反之当Loss的坡度比较平坦的时候,learning rate比较大这也符合我们的预期。结合这上面的例子可以看到,在纵轴方向应该learning rate比较小,在横轴方向learning rate比较大。那我们现在用这种,看看训练效果如何,如图所示:
可以看到这种方法还是存在缺陷,比如在经过很漫长的平滑区域积累了很大的learning rate此时很可能突然遇到陡峭的情况,但因为learning rate很大而直接跳过。或者图中震荡的区域,在一直平滑的区域,当 σ σ σ一直特别小的时候,积累到一个地步,突然爆发了这个step变得特别大,虽然后面可以经过很多修正,但浪费了很多次的update。
那我们如何改进呢,可以采用RMS Prop办法,这种办法不仅要考虑之前累计的信息,也要考虑当下的信息。其参数更新为: σ ᵢ 0 = ( g i 0 ) 2 , σ ᵢ 1 = α ( σ i 0 ) 2 + ( 1 − α ) ( g i 1 ) 2 {σᵢ^0}=\sqrt{({g_i^0})^2},{σᵢ^1}=\sqrt[]{\alpha(σ_i^0)^2+(1-\alpha)(g_i^1)^2} σᵢ0=(gi0)2,σᵢ1=α(σi0)2+(1−α)(gi1)2 σ ᵢ 2 = α ( σ i 1 ) 2 + ( 1 − α ) ( g i 2 ) 2 , σ ᵢ t = α ( σ i t − 1 ) 2 + ( 1 − α ) ( g i t ) 2 {σᵢ^2}=\sqrt[]{\alpha(σ_i^1)^2+(1-\alpha)(g_i^2)^2},{σᵢ^t}=\sqrt[]{\alpha(σ_i^{t-1})^2+(1-\alpha)(g_i^t)^2} σᵢ2=α(σi1)2+(1−α)(gi2)2,σᵢt=α(σit−1)2+(1−α)(git)2
这样根据调整 α \alpha α的值就可以设定时更关注于当下还是之前。这是一个自己设定的hyperparameter。
- 如果我今天 α α α设很小趋近於0,就代表我觉得 g ᵢ ¹ gᵢ¹ gᵢ¹相较於之前所算出来的gradient而言,比较重要
- 我 α α α设很大趋近於1,那就代表我觉得现在算出来的 g ᵢ ¹ gᵢ¹ gᵢ¹比较不重要,之前算出来的gradient比较重要
今天最常用的optimization的策略就是Adam,就是RMS Prop加上Momentum,参考论文 https://arxiv.org/pdf/1412.6980.pdf
还有一种办法也可以解决这种缺陷,叫做learning rate scheduling上个办法我们改进了 σ ᵢ σᵢ σᵢ,这次我们连着 η \eta η一起更新,将其改为 η t \eta^t ηt
其中一种learning rate scheduling叫做Learning Rate Decay,这种办法也就是说,随著时间的不断地进行,随著参数不断的update,我们这个 η η η让它越来越小,这个也就合理了,因为一开始我们距离终点很远,随著参数不断update,我们距离终点越来越近,所以我们把learning rate减小,让我们参数的更新能够慢慢地慢下来。
除了这种办法还有另外一个经典办法,也是我们现在最常用的Learning Rate Scheduling方法叫做Warm Up。
这Warm Up的方法是让learning rate,要先变大后变小,这个变大到底要变多大,变大的速度是多少,变小的速度是多少这个也是我们要自己设置的参数,也是一个hyperparameter,这个办法广泛应用于多个著名的Network,比如Transformer。这个方法实用的一个可能的解释是当我们在用Adam RMS Prop我们会需要计算 σ σ σ,它是一个统计的结果 σ σ σ告诉我们,某一个方向它到底有多陡或者是多平滑,那这个统计的结果要看得够多笔数据以后才精确,所以一开始我们的统计是不精确的,所以我们一开始不要让我们的参数离初始的地方太远,先让它在初始的地方呢做一些像是探索这样,所以一开始learning rate比较小,是让它探索收集一些有关error surface的情报,等 σ σ σ统计得比较精準以后,在让learning rate呢慢慢地爬升。
Batch Normalization
之前我们可以通过调整Training rate来解决一个error surface在横向和纵向坡度不同的问题,哪还有什么办法可以解决这个问题呢,有没有可能将本来坡度不同的error surface改称坡度近似的error surface呢?
比如假设我现在有一个非常非常非常简单的 model,它的输入是 x 1 x_1 x1 跟$ x_2,$它对应的参数就是 w 1 w_1 w1跟 w 2 w_2 w2,它是一个 linear 的 model,没有 activation function。Loss的计算公式为 ω 1 x 1 ω 2 x 2 − y \omega_1 x_1\omega_2 x_2-y ω1x1ω2x2−y
再假设 x 1 x_1 x1的范围是 1000 − 10000 1000-10000 1000−10000, x 2 x_2 x2的范围是 0 − 1 0-1 0−1,在 w 1 w_1 w1跟 w 2 w_2 w2差不多的情况下,由于 x 1 x_1 x1比较大,我们对 w 1 w_1 w1 有一个小小的改变, L 的影响也很大。反之 w 2 w_2 w2 有一个很大的改变, L 的影响也很小。这可能产生不同方向,斜率非常不同,坡度非常不同的 error surface。那我们为了避免这种情况发生,制造出近似于"圆形"(各方向平滑)的 error surface,有很多办法,统一命名为Feature Normalization,下面是一种Feature Normalization。
假设 x ⃗ 1 \vec x^1 x1 到 x ⃗ R \vec x^R xR,是我们所有的训练资料的 feature vector,我们将每一个vecter相同的dimension的向量拿出,计算他们的平均值计作 m ⃗ i \vec m_i mi,在计算他们的standard deviation(标准差),我们用 σ i σ_i σi来表示它,那接下来我们就可以做一种 normalization,那这种 normalization 其实叫做标准化,其实叫 standardization,不过我们这边呢,就等一下都统称 normalization 就好了 ,方式为: x ~ i r ← x i r − m i σ i \tilde{x}^r_i ← \frac{x^r_i-m_i}{\sigma_i} x~ir←σixir−mi然后我们将每一个 x ~ \tilde{x} x~放回每一行相应的位置,这样的好处是:
- 做完 normalize 以后,每个维度上面的数值就会平均是 0,然后它的 方差和就会是 1,所以这一排数值的分布就都会在 0 0 0 上下
- 对每一个维度都做一样的 normalization,就会发现所有 feature 不同维度的数值都在 0 上下,那因为不同 x x x的取值范围接近,可能会制造出一个好的error surface,达到训练加速的效果。
- 因为我们大多都采用Sigmoid Function,它的图象是越远离0越不敏感,存在着一定的饱和区间,这样将数据都集中在0附近可以更快更新梯度。
那我们如何继续传播normalization的参数呢?
我们将 x ~ r \tilde{x}^r x~r传到神经网络后,与 w ⃗ \vec w w相乘得到 Z ⃗ \vec Z Z,虽然我们的 x ~ r \tilde{x}^r x~r经过了Normalization,但 Z ⃗ \vec Z Z还是再不同的区间,他们的分布仍然有很大的差异的化,我们再训练下一层的时候还是会遇到相同的困难,所以我们这边要对 Z ⃗ \vec Z Z或者是 a ⃗ \vec a a也进行一次Normalization的操作,刚才说了因为你选择的是 Sigmoid,在0的附近比较敏感,所以我们选择在 Z ⃗ \vec Z Z后面进行Normalization的操作。
方法如下:那你就把 z ⃗ \vec z z,想成是另外一种 feature ,我们这边有 z ⃗ 1 z ⃗ 2 z ⃗ 3 \vec z_1 \vec z_2 \vec z_3 z1z2z3,我们就把 z ⃗ 1 z ⃗ 2 z ⃗ 3 \vec z_1 \vec z_2 \vec z_3 z1z2z3 拿出来,算一下它的 mean,这边的 μ ⃗ \vec μ μ是一个 vector,我们就把 z ⃗ 1 z ⃗ 2 z ⃗ 3 \vec z_1 \vec z_2 \vec z_3 z1z2z3,这三个 vector 算他们的平均值得到 μ ⃗ \vec μ μ,再算他们的标准差得到 σ ⃗ \vec σ σ,它也代表了一个 vector,然后 z ~ i = z ⃗ i − μ ⃗ σ ⃗ {\tilde z}^i = \frac{\vec z^i-\vec μ}{\vec \sigma} z~i=σzi−μ
这边可以看到 μ ⃗ \vec μ μ 跟 σ ⃗ \vec σ σ,它们其实都是根据 z ⃗ 1 z ⃗ 2 z ⃗ 3 \vec z_1 \vec z_2 \vec z_3 z1z2z3算出来的,本来如果我们没有做 Feature Normalization 的时候,你改变了 z ⃗ 1 \vec z_1 z1 的值,你会改变这边 a ⃗ 1 \vec a_1 a1 的值,但是现在啊,当你改变 z ⃗ 1 \vec z_1 z1的值的时候, μ ⃗ \vec μ μ 跟 σ ⃗ \vec σ σ 也会跟著改变, μ ⃗ \vec μ μ 跟 σ ⃗ \vec σ σ改变以后 z ⃗ 2 z ⃗ 3 \vec z_2 \vec z_3 z2z3的值, a ⃗ 2 \vec a_2 a2 a ⃗ 3 \vec a_3 a3的值,也会跟着改变。
我们以前每一个 x ~ 1 \tilde{x}_1 x~1 x ~ 2 \tilde{x}_2 x~2 x ~ 3 \tilde{x}_3 x~3它是独立分开处理的,但是我们在做 Feature Normalization 以后,这三个 example,它们变得彼此关联了。
但是因为训练资料裡面的 data 非常多,GPU没法考虑所有的值再计算 μ ⃗ \vec μ μ 跟 σ ⃗ \vec σ σ,只能考虑每一个Batch的值分别计算其 μ ⃗ \vec μ μ 跟 σ ⃗ \vec σ σ,如果一个epoch里有64个Batch,那么我们就要计算64个 μ ⃗ \vec μ μ 跟 σ ⃗ \vec σ σ,所以这招叫做 Batch Normalization。实际的计算中往往还有一个操作:
- 接下来你会把这个 z ~ \tilde{z} z~,再乘上另外一个向量叫做 γ ⃗ \vec γ γ,这个 γ ⃗ \vec γ γ也是一个向量,所以你就是把 z ~ \tilde{z} z~跟 γ ⃗ \vec γ γ做 element wise的相乘,也就是对应元素逐个相乘。
- 再加上 β β β 这个向量,得到 z ^ \hat {z} z^。
z ^ i = γ ⃗ ⨀ z ~ i + β \hat {z}^i=\vec γ\bigodot\tilde{z}^i+β z^i=γ⨀z~i+β
那为什么要加上 β β β 跟 γ γ γ 呢,如果我们做 normalization 以后,那这边的 z ^ \hat z z^,它的平均就一定是 0那也许,今天如果平均是 0 的话,就是给那 network一些限制,也许这个限制会带来什么负面的影响,所以我们把 β 跟 γ 加回去,后面network会自己调整 β 跟 γ的值。
但这不是和之前我们初衷相背离了嘛,我们之前就是想要他们保持在0附近并且range一样。其实没有,我们最开始的时候 β β β 的初始值里面全部都是0向量, γ γ γ 就是里面全部都是1的向量,所以在训练开始阶段每一个dimension 的分布是比较接近的,但训练一段时间后已经找到一个比较好的 error surface,那再把 γ γ γ 跟 β β β 学习出其他的值慢慢地加进去。
上面说的都是Training过程的Batch Normalization,那再Testing过程中,很可能数据不是一个Batch一个Batch传过来的,比如我每次Training的过程每一个Batch有64个照片,现在我只输入一个照片让其识别,那刚才我们的 μ ⃗ \vec μ μ 跟 σ ⃗ \vec σ σ是根据一个Batch算出来的啊,我们现在根本都没有一个Batch的数据。PyTorch为我们提供的方案是moving average
- 将训练集计算出的每一个 μ μ μ取出计为 μ i μ^i μi,计算所有 μ μ μ的平均值,记成 μ ˉ \bar μ μˉ,第 t t t次的更新公式为 μ ˉ ← p μ ˉ + ( 1 − p μ t ) \bar μ\leftarrow p\bar μ+(1-pμ^t) μˉ←pμˉ+(1−pμt)
- 这个 p p p是一个hyper parameter,PyTorch中设置为0.1.
- σ ⃗ \vec σ σ的计算方式和 μ ⃗ \vec μ μ 相同。得到 μ ˉ 和 σ ˉ \bar μ 和\bar σ μˉ和σˉ后这两个值就是运算testing set的时候对应的值。
综上所述,今天解决了三个问题,Batch大小的选择问题,随着模型更新Learning Rate如何适应性改变的问题,如何让模型在各个维度上梯度接近的问题。