投影波峰查找

波峰波谷算法

投影曲线实际上是一个一维的向量：

V=[v1,v2,…,vn]

其中 vi,i∈[1,2,…,N]，代表图像在第 i行或列上的灰度累积。当然不仅仅是投影曲线， T也可以是某一事件中变量的观测值，我们需要研究这个变量的变化规律。

下面给出波峰与波谷的算法：

1，假投影曲线可以表示为 V=[v1,v2,…,vn]。

2，计算V的一阶差分向量 DiffV:

其中 Diffv(i)=V(i+1)−V(i),其中i∈1,2,…,N−1

3,对差分向量进行取符号函数运算， Trend=sign(Diffv),即遍历 Diffv，若 Diffv(i)大于0，则取1；如果小于0，则取-1，否则则值为0。

sign(x)={1  if  x>00  if  x=0−1  if  x<0

4，从尾部遍历 Trend向量,进行如下操作：

if Trend(i)=0且Trend(i+1)≥0，则Trend(i)=1 if Trend(i)=0且Trend(i+1)<0，则Trend(i)=−1

5，对 Trend向量进行一阶差分运算，如同步骤2，得到 R=diff(Trend)。

6，遍历得到的差分向量 R，如果 R(i)=−2，则 i+1为投影向量 V的一个峰值位，对应的峰值为 V(i+1)；如果 R(i)=2，则 i+1为投影向量 V的一个波谷位，对应的波谷为 V(i+1)。

下面我们来结合一个实际的向量值，给中中间结合的计算。

1， V=[−5,10,10,14,14,8,8,6,6,−3,2,2,2,2,−3]。

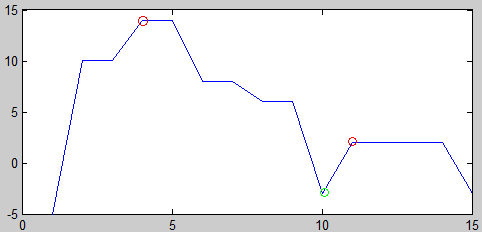
它的曲线图像如下把示，图中红色圈标出了曲线的峰值，而绿字圈标出了图像的波谷位置。

2，计算 V的一阶差分，我们得到 Diff(V)=[15,0,4,0,,−6,0,−2,0,−9,5,0,0,0,−5]。

3，对 Diffv进行取符号运算，得到向量 Trend=[1,0,1,0,−1,0,−1,0,−1,1,0,0,0,−1]。

4，对 Trend作一次遍历，如步骤4。 Trend=[1,1,1,−1,−1,−1,−1,−1,−1,1,−1,−1,−1,−1]。

5，对 Trend做一阶差分，得到向量 R=Diff(Trend)=[0,0,−2,,0,0,0,0,0,2,−2,0,0,0]。

6，遍历向量 R,我们就得到了两个峰值点和一个波谷点。

算法原理

其实上述算法的核心思路非常简单，曲线的峰值点，满足一阶导数为0，并且满足二阶导数为负；而波谷点，则满足一阶导数为0，二阶导数为正。

在上面的算法里面，我们首先计算了一阶的导数 Diffv，然后我们将其符号化，是因为我们并不关心一阶导数的大小。

然后我们去看那些一阶层数为0的地方，我们发现，那些平台上的点，有些并不是波峰与波谷，然后很多处在上坡与下坡的路上，所以我们将它们的一阶导数设为与它们所在的坡面梯度方向相同。

最后我们再来计算二阶导数时，就会发现只要为2或者-2,所以曲线斜在这个点发生了变化，由正变负或由负变正。找到这些点，也就找到了原曲线中的波峰或波谷点。

代码实现：

#include
#include
#include
#include
#include
using namespace cv;
using namespace std;
void findpeak(Mat &srcImage, vector& resultVec)
{
	Mat verMat;
	Mat resMat = srcImage.clone();

	
	int thresh = 130;
	int threshType = 0;
	
	
	const int maxVal = 255;
	
	threshold(srcImage, srcImage, thresh, maxVal, threshType);

	
	srcImage.convertTo(srcImage, CV_32FC1); 
	reduce(srcImage, verMat, 0, CV_REDUCE_SUM);
	float* iptr = (float*)verMat.data;
	vector tempVec(verMat.cols - 1, 0);

	
	for (int i = 0; i < verMat.cols - 1; ++i, ++iptr)
	{
		if(*(iptr+1) - *iptr > 0)
		{
			tempVec[i] = 1;
		}
		else if (*(iptr + 1) - *iptr < 0)
		{
			tempVec[i] = -1;
		}
		else
		{
			tempVec[i] = 0;
		}
	}

	
	for (int i = tempVec.size() - 1; i >= 0; i--)
	{
		if (tempVec[i] == 0 && i == tempVec.size() - 1)
		{
			tempVec[i] = 1;
		}
		else if (tempVec[i] == 0)
		{
			if (tempVec[i + 1] >= 0)
				tempVec[i] = 1;
			else
				tempVec[i] = -1;
		}
	}

	
	for (vector::size_type i = 0; i != tempVec.size() - 1; i++)
	{
		if (tempVec[i + 1] - tempVec[i] == -2)
		{
			resultVec.push_back(i + 1);
		}
	}

	
	for (int i = 0; i < resultVec.size(); i++)
	{
		cout << resultVec[i] << endl;
		for (int ii = 0; ii < resMat.rows; ++ii)
		{
			resMat.at(ii, resultVec[i]) = 255;
		}
	}
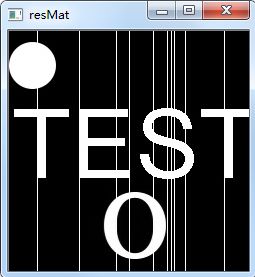
	imshow("resMat", resMat);
}
int main()
{
	Mat image = imread("test.jpg");
	if (!image.data)
	{
		printf("could not load image...\n");
		return -1;
	}
	
	cvtColor(image, image, CV_BGR2GRAY);
	imshow("image", image);
	vector resultVec;
	findpeak(image, resultVec);
	waitKey(0);
	return 0;
}

波峰的位置：

28 70 107 120 144 158 162 165 176 215

原图的灰度图：

效果图：