算法通关村第六关白银挑战——树的层序遍历和它的相关例题原来如此简单
大家好, 我是怒码少年小码。
今天主要分享一下如何实现层序遍历以及它的相关基础题目。
什么是层序遍历
顾名思义,按照层序实现树的遍历。(一般来说是从上至下,从左到右,这符合中国人的阅读习惯)例如,如图的二叉树:
1
/ \
2 3 它的层序遍历结果:
/ \ / 1、2、3、4、5、6
4 5 6
如何实现层序遍历
以层的角度看问题,我们只需要用一个数据结构保存当前访问层的所有结点,将当前层的所有结点的左右孩子保存到另外一个数据结构中,下一次的时候就从另外一个数据结构中取出要访问的结点。
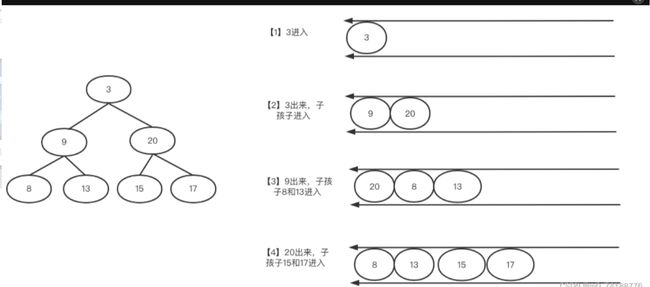
由此可见,该数据的存取顺序是一样的,所以我们选择队列。如图:
- 先3入队,
- 然后3出队,将3的左右孩子9、20入队;
- 然后9、20出队,9的左右孩子8、13,20的左右孩子15、17入队
- 最后8 13 15 17出队,由于没有孩子了,队列也就为空,层次遍历也就结束了
最后这个队列的出队顺序就是层序遍历的结果,我们可以用一个一维数组保存一下每次的出队结果,最后用一个二位数组保存整个的遍历结果。
例如,上图的二叉树层序遍历的结果用二维数组保存:
[ [3],[9,20],[8,13,15,17]]
代码实现如下:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ret;// 存储层序遍历结果的二维数组
if (!root) {
return ret; // 如果二叉树为空,直接返回空的结果
}
queue<TreeNode*> q; // 用于遍历的队列
q.push(root);// 将根结点加入队列
while (!q.empty()) {
int currentLevelSize = q.size();
ret.push_back(vector<int>());// 每层开始时创建一个新的空白数组
for (int i = 0; i <= currentLevelSize; i++) {
auto node = q.front();// 取出队首结点
q.pop();// 弹出队首结点
cout << node->val << " ";
ret.back().push_back(node->val);//back()返回vector的最后一个元素的引用(也就是当前层的数组) 将结点的值加入到当前层的数组中
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
}
}
return ret;
}
相关例题
想一想既然都能得到每一层的结点了,你能不能玩出新花样?就每一层的最大结点?按照奇偶遍历层序?能否将某一层的结点反转?
这就是层序遍历算法题的本质:在层序遍历的基础上改进罢了。接下来我们看几道经典的题目。
自底向上遍历
LeetCode 107:给你二叉树的根结点 root,返回其结点值自底向上的层序遍历。(即按从叶子结点所在层到根结点所在的层,逐层从左向右遍历)
这不就是把普通遍历的二维数组反转一遍吗?easy!
vector<vector<int>> ret;// 存储层序遍历结果的二维数组
if (!root) {
return ret; // 如果二叉树为空,直接返回空的结果
}
queue<TreeNode*> q; // 用于遍历的队列
q.push(root);// 将根结点加入队列
while (!q.empty()) {
int currentLevelSize = q.size();
ret.push_back(vector<int>());// 每层开始时创建一个新的空白数组
for (int i = 0; i <= currentLevelSize; i++) {
auto node = q.front();// 取出队首结点
q.pop();// 弹出队首结点
cout << node->val << " ";
ret.back().push_back(node->val);//back()返回vector的最后一个元素的引用(也就是当前层的数组) 将结点的值加入到当前层的数组中
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
}
}
//反转数组
reverse(ret.begin(),ret.end());
return ret;
找到数行的最大值
LeetCode 515:给定一棵二叉树的根结点 root ,请找出该二叉树中每一层的最大值。
思路:队列中保存每一层的所有结点,我们只需要在出队的时候比较一下值的大小,再把最大值插入数组的末尾就可以,本题没必要用到二维数组。
vector<int> findBig(TreeNode* root) {
vector<int> ret;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
int levelSize = q.size();
int maxNode = INT_MIN;
while (levelSize > 0) {
levelSize--;
TreeNode* cur = q.front();
q.pop();
// 更新当前层的最大值
maxNode = max(maxNode, cur->val);
if (cur->left) q.push(cur->left);
if (cur->right) q.push(cur->right);
}
ret.push_back(maxNode); //将当前层的最大值保存
}
return ret;
}
在每个树行中找平均值
LeetCode 638:给定一个非空二叉树的根结点 root , 以数组的形式返回每一层结点的平均值。
思路:队列中保存每一层的所有结点,我们只需要记录一下队列的大小(size),并在出队的时候累加一下结点的值(sum),就能计算平均值。
vector<double> findArg(TreeNode* root) {
vector<double> ret;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
double sum = 0;
int levelSize = q.size();
int size = levelSize;
while (levelSize > 0) {
levelSize--;
TreeNode* cur = q.front();
q.pop();
sum = sum + cur->val;
if (cur->left) q.push(cur->left);
if (cur->right) q.push(cur->right);
}
ret.push_back(sum / size);
}
return ret;
}
二叉树的右视图
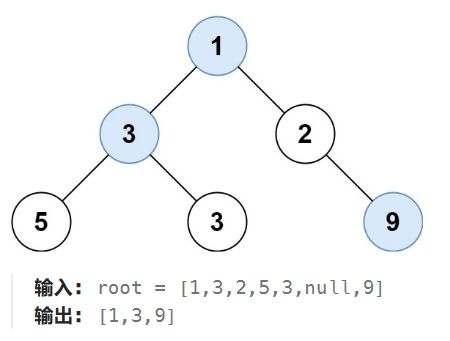
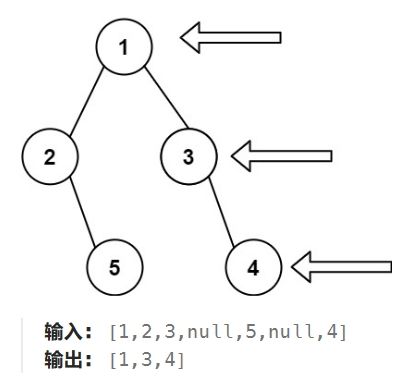
LeetCode 199:给定一个二叉树的 根结点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的结点值。
思路:上图的层序遍历的二维数组是[[1],[2,3],[5,4]],而右视图应该返回的是[1,3,4]。观察一下,不难发现我们应该用一个数组(ret)保存每一层出队后的一维数组(temp)的最后一个元素。
vector<int> seeRight(TreeNode* root) {
vector<int> ret;
vector<int> temp;
queue<TreeNode*> q;
q.push(root);
ret.push_back(root->val);
while (!q.empty()) {
int len = q.size();
while (len > 0) {
TreeNode* cur = q.front();
q.pop();
temp.push_back(cur->val);
if (cur->left) q.push(cur->left);
if (cur->right) q.push(cur->right);
}
ret.push_back(temp.back());
}
return ret;
}
找到树最左下角的值
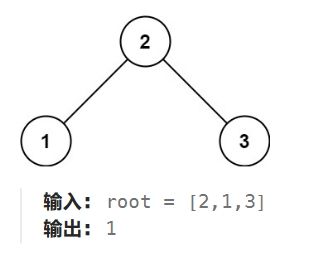
LeetCode 513:给定一个二叉树的 根结点 root,请找出该二叉树的最底层最左边结点的值。假设二叉树中至少有一个结点。
思路:显然,在层序遍历最后生成的二维数组中,最底部的一层也就是最后一个一维数组,最底部的一层的最左的结点也就是该一维数组的第一个元素。
int findLeft(TreeNode* root) {
vector<vector<int>> ret;// 存储层序遍历结果的二维数组
if (!root) {
return 0; // 如果二叉树为空,直接返回空的结果
}
queue<TreeNode*> q; // 用于遍历的队列
q.push(root);// 将根结点加入队列
while (!q.empty()) {
int currentLevelSize = q.size();
ret.push_back(vector<int>());// 每层开始时创建一个新的空白数组
for (int i = 0; i <= currentLevelSize; i++) {
auto node = q.front();// 取出队首结点
q.pop();// 弹出队首结点
cout << node->val << " ";
ret.back().push_back(node->val);//back()返回vector的最后一个元素的引用(也就是当前层的数组) 将结点的值加入到当前层的数组中
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
}
}
return ret.back()[1];
}
END
啊~一早上连刷四题,爽!