数据集：男女身高体重（二维）

数据集：男女身高体重（二维）

本文讨论该数据集的Bayes和MSE分类器的设计。
前导知识文献：【正态分布下贝叶斯决策的特例（三）】、【最小平方误差判别（MSE）】

Bayes判别分类器

1. 预处理

# 导包
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd # 表格处理
import math # 数学计算
import sympy as sp # 绘图

# 导入数据
train_data = pd.read_excel('traindata.xlsx')
test_data = pd.read_excel('testdata.xlsx')

# 拆分数据集:1代表男性,-1代表女性
train_data_men = train_data.iloc[0:50,1:3]
train_data_women = train_data.iloc[50:100,1:3]
test_data_men = test_data.iloc[0:50,1:3]
test_data_women = test_data.iloc[50:100,1:3]

预处理的目的为便于后续处理训练样本数据

2. 计算训练样本的均值

n = 50
mu_men = np.sum(np.array(train_data_men),axis=0)/n
mu_women = np.sum(np.array(train_data_women),axis=0)/n

mu_men：

174.134
66.608

mu_women：

161.03
51.956

3. 计算各类协方差矩阵

A = np.array(train_data_men)-mu_men
B = np.transpose(A)
sigma_men = np.dot(B,A)/n

A = np.array(train_data_women)-mu_women
B = np.transpose(A)
sigma_women = np.dot(B,A)/n

sigma_men：

20.4958	2.20953
2.20953	70.5663

sigma_women：

19.6617	9.33412
9.33412	29.1861

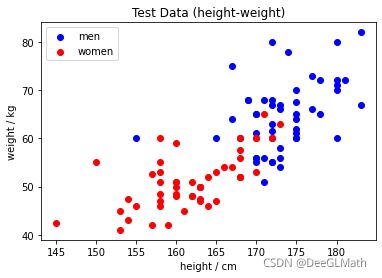
4. 绘制测试数据散点图

plt.scatter(test_data_men['height'],test_data_men['weight'],c='b',label='men')
plt.scatter(test_data_women['height'],test_data_women['weight'],c='r',label='women')
plt.legend();
plt.xlabel('height / cm')
plt.ylabel('weight / kg')
plt.title('Test Data (height-weight)')
plt.show()

图示：

5. 计算分类器分类测试数据产生的错误率

const1 = -0.5*math.log(np.linalg.det(sigma_men)/np.linalg.det(sigma_women))
sigma_men_inv = np.linalg.inv(sigma_men)
sigma_women_inv = np.linalg.inv(sigma_women)
x = np.array(test_data.iloc[:,1:3])
scores = 0
for i in range(2*n):
    x1 = x[i]-mu_men
    x2 = x[i]-mu_women
    g1 = (x1.dot(sigma_men_inv)).dot(x1.transpose())
    g2 = (x2.dot(sigma_women_inv)).dot(x2.transpose())
    curve = -0.5*(g1-g2) + const1
    if ((curve>0)&(test_data['gender'][i]==1))|((curve<0)&(test_data['gender'][i]==-1)):
        scores += 1
print('errorRate:',1-scores/100)

结果：

errorRate: 0.08999999999999997

6. 确定分类线区间并绘制分类线

xmin = test_data_women['height'].min() - 20
xmax = test_data_men['height'].max() + 20
ymin = test_data_women['weight'].min() - 20
ymax = test_data_men['weight'].max() + 20
fig,ax = plt.subplots(1,1)
ax.scatter(test_data_men['height'],test_data_men['weight'],c='b',label='men')
ax.scatter(test_data_women['height'],test_data_women['weight'],c='r',label='women')
x = sp.Symbol('x')
y = sp.Symbol('y')
X = np.array([x,y])
x1 = X - mu_men
x2 = X - mu_women
fin = -0.5*((x1.dot(sigma_men_inv)).dot(x1.transpose())-(x2.dot(sigma_women_inv)).dot(x2.transpose())) + const1
print(sp.simplify(fin))
xx,yy = np.linspace(xmin,xmax,15),np.linspace(ymin,ymax,15)
x,y = np.meshgrid(xx,yy)
ax.legend()
ax.contour(x,y,(0.00550446923228119*x**2 - 0.0176446572158389*x*y - 0.236968574102361*x + 0.013088557295945*y**2 + 1.66951194856611*y - 85.0026770450582),[0])
plt.show()

结果：

0.00550446923228119*x**2 - 0.0176446572158389*x*y - 0.236968574102361*x + 0.013088557295945*y**2 + 1.66951194856611*y - 85.0026770450582

图示：

MSE线性分类器

1.预处理

# 导包
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import sympy as sp # 绘图

# 导入数据
train_data = pd.read_excel('traindata.xlsx')
test_data = pd.read_excel('testdata.xlsx')

# 预处理数据
X = np.ones([100,3])
X[:,1:3] = train_data.iloc[:,1:3]
y = np.array(train_data['gender'])

y中数据为分类标签：+1或-1

2. 伪逆法求解参数

theta = ((np.linalg.inv((X.T).dot(X))).dot(X.T)).dot(y)

结果：

-14.9076
0.0783155
0.0300815

3. 绘制测试数据散点图和决策线

xmin = test_data['height'].min() - 20
xmax = test_data['height'].max() + 20
ymin = test_data['weight'].min() - 20
ymax = test_data['weight'].max() + 20
fig,ax = plt.subplots(1,1)
ax.scatter(test_data['height'][0:50],test_data['weight'][0:50],c='b',label='men')
ax.scatter(test_data['height'][50:100],test_data['weight'][50:100],c='r',label='women')
x = sp.Symbol('x')
y = sp.Symbol('y')
fin = theta[0]+theta[1]*x+theta[2]*y
print(sp.simplify(fin))
xx,yy = np.linspace(xmin,xmax,15),np.linspace(ymin,ymax,15)
x,y = np.meshgrid(xx,yy)
ax.legend()
ax.contour(x,y,(0.0783155197575863*x + 0.0300815202467307*y - 14.9075641152825),[0])
plt.show()

结果：

0.0783155197575863*x + 0.0300815202467307*y - 14.9075641152825

图示：

4. 对测试集计算错误率

scores = 0
for i in range(100):
    t1 = 0.0783155197575863*test_data.iloc[i,1] + 0.0300815202467307*test_data.iloc[i,2] - 14.9075641152825
    if ((t1 > 0)&(test_data.iloc[i,0]==1))|((t1 < 0)&(test_data.iloc[i,0]==-1)):
        scores += 1
print('errorRate:',1-scores/100)

结果：

errorRate: 0.08999999999999997