【路径规划】Dijkstra算法——超详细原理图解

1. Dijkstra算法原理

 1.1. 有向图的Dijkstra算法

  网上关于Dijkstra算法的文章纷繁复杂，有的在算法流程上有一些问题或谬误，有的并没有明确解释算法的详细流程，有的只介绍了简单的流程步骤，没有后续迭代的步骤。所以我决定将该算法的彻底完整流程以图表配文的形式详细描述一遍，希望能给有需要的人带来帮助。
  Dijkstra算法在最短路径问题上有着十分稳定、准确的最短路径搜索结果，是十分经典的路径规划算法，其基础理论也作为许多最短路径算法的基础，那么我们就来图解一下Dijkstra算法的具体流程：
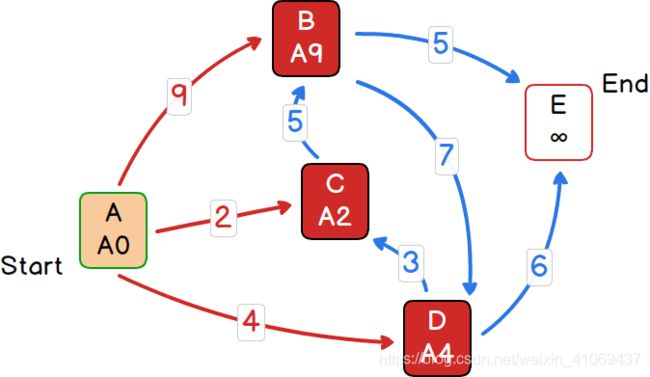
  以下图5节点带权边的有向图为例：

open	A	B	C	D	E
closed

  A为路径起点，E为路径终点，每个节点含2个信息，第1个是在从起点到该节点的当前最短路径上，该节点的父节点，初始化为自身；第2个是从起点到该节点的当前最短路径长度。
  同时算法要维护两个集合，open开集集合和closed闭集集合，open开集集合存储还未确定到达起点的最短路径的节点，初始化包含所有点集，closed闭集集合存储已经确定了到达起点的最短路径的节点，初始化为空集合。
  第一步：

open		B	C	D	E
closed	A

  1）将起点A从open集合中去除并加入closed集合。
  2）计算并更新在open集合中起点A可达的节点B、C、D到起点A的距离，并更新这些节点的父节点为A，并将剩余节点E的父节点置为空或自身皆可，将其距离值置为正无穷大或一个足够大的数。
  第二步：

open		B		D	E
closed	A		C

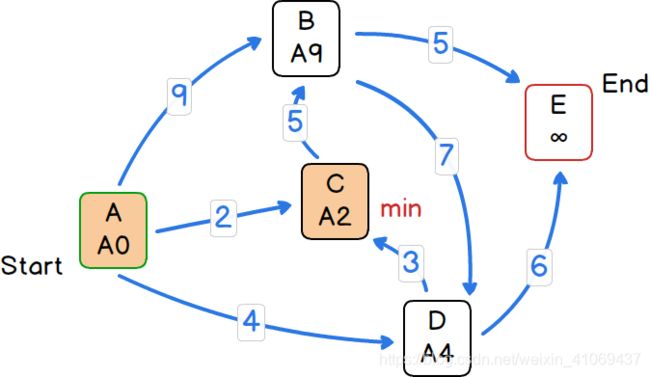
  1）选取open集合中距离起点A的最短路径长度最小的节点C，将其从open集合中去除并加入closed集合中。
  第三步：

open		B		D	E
closed	A		C

  1）从上一步选出的节点C出发，计算所有其可达的并在open集合中的节点B，更新B的最短路径长度和父节点，当前B的最短路径距离为9，父节点为A，而若从C出发到达B，则最短路径长度将减小为7，符合更新条件，所以将B的最短路径长度更新为7，其父节点更新为C。
  第四步：

open		B			E
closed	A		C	D

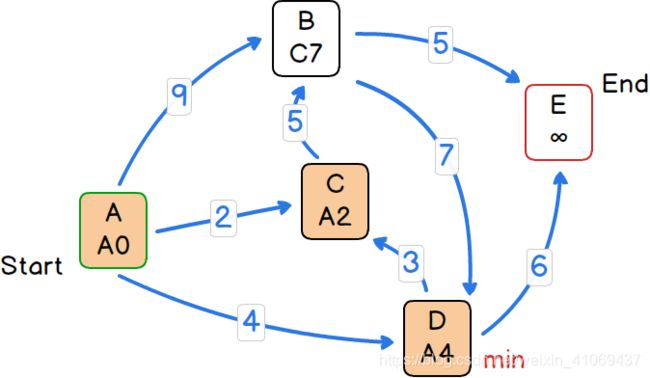
  1）选取open集合中距离起点A的最短路径长度最小的节点D，将其从open集合中去除并加入closed集合中。
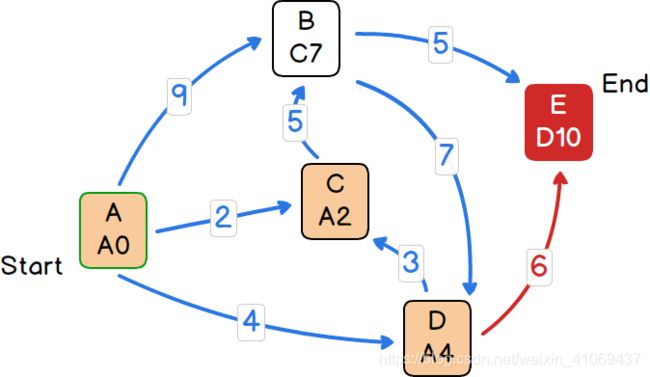
  第五步：

open		B			E
closed	A		C	D

  1）从上一步选出的节点D出发，计算所有其可达的并在open集合中的节点E，由于当前E还未更新最短路径长度和父节点，所以直接更新E的最短路径长度和父节点为10和D。
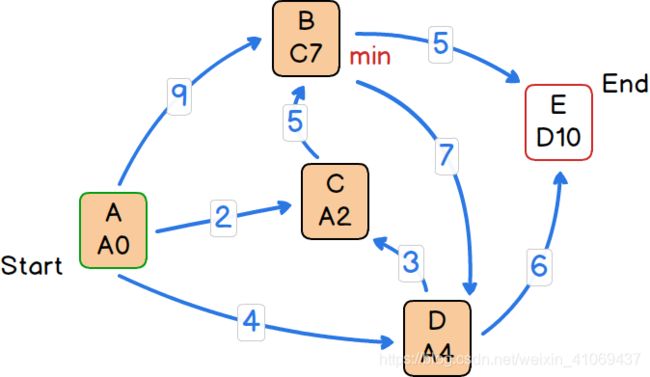
  第六步：

open					E
closed	A	B	C	D

  1）选取open集合中距离起点A的最短路径长度最小的节点B，将其从open集合中去除并加入closed集合中。
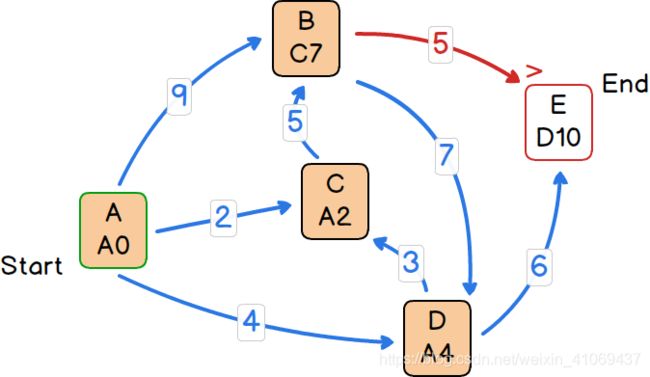
  第七步：

open					E
closed	A	B	C	D

  1）从上一步选出的节点B出发，计算所有其可达的并在open集合中的节点E，当前E节点的最短路径长度为10，其父节点为D，而A经过B到达E的话，其路径长度为12，大于E原有的最短路径长度，不符合更新条件，所以对E的更新失败，E仍然保留原有的最短路径长度和父节点。
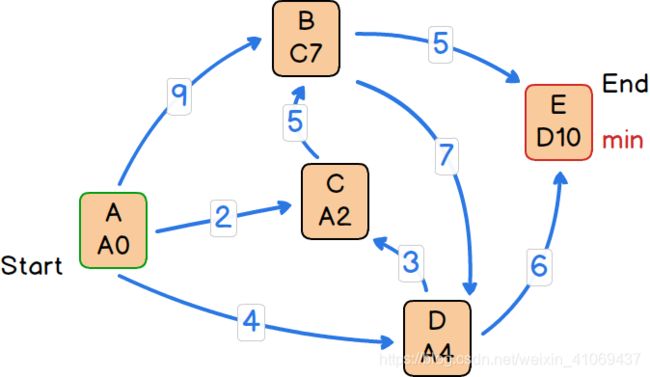
  第八步：

open
closed	A	B	C	D	E

  1）选取open集合中距离起点A的最短路径长度最小的节点E，将其从open集合中去除并加入closed集合中。
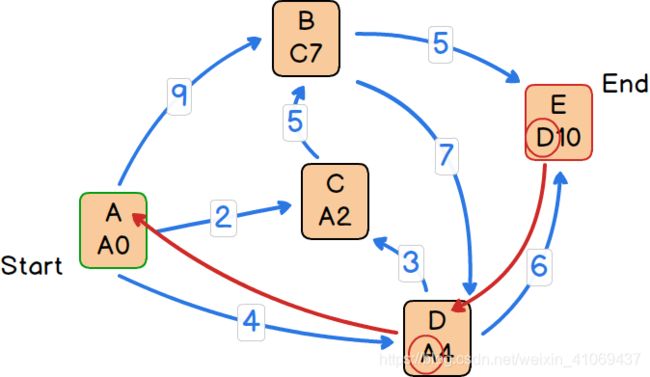
  第九步：

open
closed	A	B	C	D	E

  1）由于目标点E已经被加入closed闭集合中，所以算法迭代中止，已经找到了从A到E的最短路径。
  2）从路径终点E开始，根据父节点逆推路径可以得到，从A到E的最短路径是A-D-E，其最短路径长度为10。
  至此，带权边的有向图中单源最短路径已经找到，Dijkstra算法的整个运行流程也便是如此。相信这样的图解已经十分详细表现了Dijkstra算法的运行流程啦。

 1.2. 无向图和栅格网络的拓展

  1.2.1. 无向图

  无向图的Dijkstra算法只需要在上述有向图的算法中进行拓展，算法差别只是在每一次从选定节点向外搜索可达节点并更新的环节上，无向图中可以选择所有open集合中与选定节点相连的节点，可拿上述过程的第二步和第三步做直观比较：
  “第二步：”

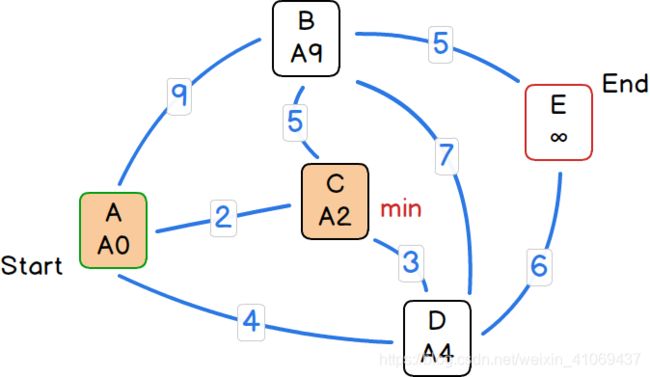
  “第三步：”

  面向无向图的拓展改进是好理解并好实现的，而在机器路径规划时常用到的栅格网络，则是无向图的一种特例，是一种规则化等权边的无向图。

  1.2.2. 栅格网络

  栅格网络常用在对机械运动的构型空间的建模中，用于进行路径规划，而栅格网络可以理解成规则排布的一个个节点，每个连边的权重为1：

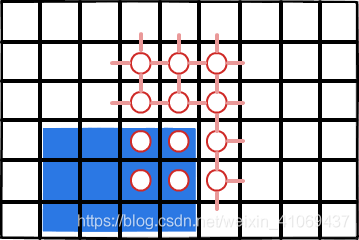
  利用这样的等效，将自由空间节点和障碍物节点根据空间情况进行划分和构建，就可以使用Dijkstra算法在栅格化的构型空间中寻找出机械运作或移动的最短路径。

2. Dijkstra程序实现

  程序范例以上文提到的例子进行测试：

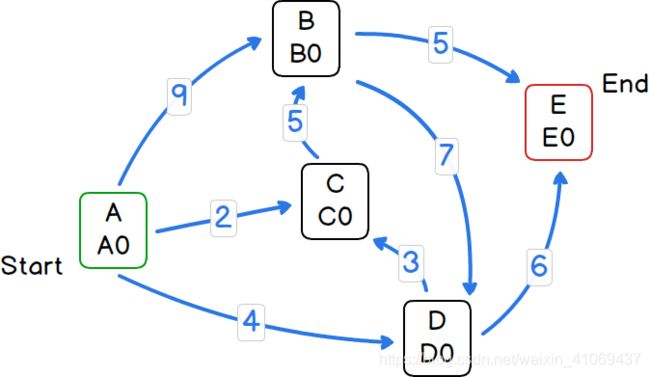
根据该图，可以创建输入数据文本：

 Java

  代码：

//Dijkstra算法
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;
import java.util.Iterator;

public class Main {
    public static void main(String[] args) {
        String fileName = "demo.txt";
        Character startPoint = 'A';
        Character endPoint = 'E';
        File file = new File(fileName);
        BufferedReader reader = null;
        String tempString = null;
        HashMap<Character, ArrayList<TwoTuple<Character, Integer>>> connects = new HashMap<>();
        try {
            reader = new BufferedReader(new FileReader(file));
            while (null != (tempString = reader.readLine())) {
                String[] tempStrSplit = tempString.split(" ");
                TwoTuple<Character, Integer> tempTwoTuple = new TwoTuple<>(tempStrSplit[1].charAt(0), Integer.parseInt(tempStrSplit[2]));
                if (connects.containsKey(tempStrSplit[0].charAt(0))) { //连接集合已经含有该点出边
                    ArrayList<TwoTuple<Character, Integer>> tempArr = connects.get(tempStrSplit[0].charAt(0));
                    tempArr.add(tempTwoTuple);
                    connects.replace(tempStrSplit[0].charAt(0), tempArr);
                } else { //连接集合未含该点出边
                    ArrayList<TwoTuple<Character, Integer>> tempArr = new ArrayList<>();
                    tempArr.add(tempTwoTuple);
                    connects.put(tempStrSplit[0].charAt(0), tempArr);
                }
            }
            reader.close();
        } catch (Exception e) {
            e.printStackTrace();
        }
        TwoTuple<Character[], Integer> res = DijkstraMethod(connects, startPoint, endPoint); //获得最短路径结果
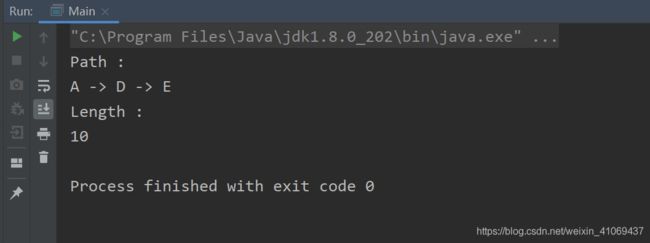
        System.out.println("Path :"); //打印最短路径结果
        for (int i = 0; i < res.fst.length - 1; i++) {
            System.out.print(res.fst[i] + " -> ");
        }
        System.out.println(res.fst[res.fst.length - 1]);
        System.out.println("Length :");
        System.out.println(res.snd);
    }
    public static TwoTuple<Character[], Integer> DijkstraMethod(HashMap<Character, ArrayList<TwoTuple<Character, Integer>>> source, Character startPoint, Character endPoint) {
        ArrayList<Character> open = new ArrayList<>();
        ArrayList<Character> closed = new ArrayList<>();
        HashSet<Character> points = new HashSet<>( );
        source.forEach((k, v) -> { //获得所有点集
            points.add(k);
            v.forEach(x -> {
                points.add(x.fst);
            });
        });
        Character[] allPoints = new Character[points.size()];
        Character[] fatherPoints = new Character[points.size()];
        int[] dists = new int[points.size()];
        int[] distRes = new int[points.size()];
        int k = 0;
        for (Iterator<Character> iterator = points.iterator(); iterator.hasNext(); ) { //将点集转化为字符数组形式
            Character thisChar = iterator.next();
            open.add(thisChar); //添加开集
            allPoints[k] = thisChar; //初始化节点数组
            fatherPoints[k] = thisChar; //初始化父节点数组
            dists[k] = Integer.MAX_VALUE; //初始化距离数组
            k++;
        }
        k = findIndex(allPoints, startPoint);
        dists[k] = 0;
        int tempIndex = 0;
        while (open.contains(endPoint)) { //开集有终点则一直继续寻找轨迹
            k = findMinNumIndex(dists); //找到当前距离最小节点
            open.remove(allPoints[k]); //从开集中移除
            closed.add(allPoints[k]); //加入闭集
            distRes[k] = dists[k]; //将最终距离存储
            dists[k] = -1; //距离置为-1，不参与最小值判断
            if (allPoints[k].equals(endPoint)) { //若终点被移除，则停止迭代
                break;
            }
            ArrayList<TwoTuple<Character, Integer>> thisPointConnect = source.get(allPoints[k]);
            for (int i = 0; i < thisPointConnect.size(); i++) {
                tempIndex = findIndex(allPoints, thisPointConnect.get(i).fst);
                if (distRes[k] + thisPointConnect.get(i).snd < dists[tempIndex]) { //符合更新条件
                    fatherPoints[tempIndex] = allPoints[k];
                    dists[tempIndex] = distRes[k] + thisPointConnect.get(i).snd;
                }
            }
        }
        //输出路径和距离
        k = findIndex(allPoints, endPoint);
        ArrayList<Character> output = new ArrayList<>();
        output.add(endPoint);
        while (!allPoints[k].equals(startPoint)) {
            output.add(fatherPoints[k]);
            k = findIndex(allPoints, fatherPoints[k]);
        }
        Character[] outChars = new Character[output.size()];
        for (int i = 0; i < output.size(); i++) {
            outChars[i] = output.get(output.size() - 1 - i);
        }
        k = findIndex(allPoints, endPoint);
        TwoTuple<Character[], Integer> res = new TwoTuple<>(outChars, distRes[k]);
        return res;
    }
    public static int findIndex(Character[] chars, Character charOne) {
        for (int i = 0; i < chars.length; i++) {
            if (chars[i].equals(charOne)) {
                return i;
            }
        }
        return -1;
    }
    public static int findMinNumIndex(int[] ints) {
        int minNum = Integer.MAX_VALUE;
        int minNumIndex = 0;
        for (int i = 0; i < ints.length; i++) {
            if (ints[i] < minNum && ints[i] >= 0) {
                minNum = ints[i];
                minNumIndex = i;
            }
        }
        return minNumIndex;
    }
}
class TwoTuple<K, V> {
    public final K fst;
    public final V snd;
    TwoTuple(K k, V v){
        fst = k;
        snd = v;
    }
}

  结果：