数据结构学习笔记（第三章 栈，队列和数组）

目录

​编辑

一、栈

1.定义

2.基本操作（严蔚敏版）

 3.栈的顺序存储结构

顺序栈的实现

栈的基本运算

 共享栈

 4.栈的链式存储

 二、队列

1.定义

2.基本操作

 3.队列的顺序存储

循环队列

4.队列的链式存储结构

基本操作

 5.双端队列

 三、数组

 1.定义

2.特殊矩阵的压缩存储

---

 

一、栈

1.定义

栈是只允许在一端进行插入和删除操作的线性表。

栈顶：线性表允许插入删除的一端。

栈底：固定的，不允许插入删除的另一端。

空栈：不含任何元素的空表。

栈的特性：符合后进先出算法（Last In First Out ,LIFO）

2.基本操作（严蔚敏版）

 3.栈的顺序存储结构

顺序栈的实现

栈顶指针：S.top，初始时设置为S.top=-1;栈顶元素：S.data[S.top]

进栈：栈不满时，栈顶指针先加一，再送值到栈顶元素。

出栈：栈非空时，先取栈顶元素值，再将栈顶指针减一。

栈空条件：S.top==-1，栈满条件：S.top==MaxSize-1，栈长：S.top+1

栈的基本运算

初始化
void InitStack(SqStack &S){
    S.top=-1;
}


判断栈空
bool StackEmpty(SqStack S){
    if(S.top==-1)//栈空
        return true;
    else
        return false;
}

入栈：
bool Push(SqStack &S,ElemType x){
    if(S.top==MaxSize-1)//栈满，报错
        return false;
    S.data[++S.top]=x;//先加一，再进栈
    return true;
}

出栈：
bool Pop(SqStack &S,ElemType &x){
    if(S.top==-1)//栈空，报错
        return false;
    x=S.data[S.top--];//先出栈，再减一
    return true;
}

读栈顶元素
bool GetTop(SqStack S,ElemType &x){
    if(S.top==-1)
        return false;
    x=S.data[S.top];//读
    return true;
}

 共享栈

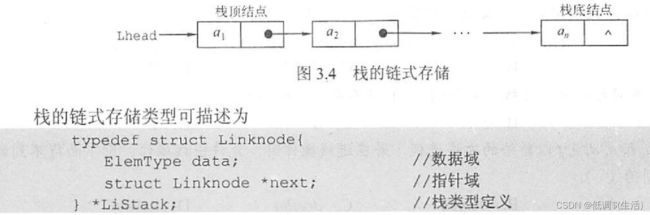
 4.栈的链式存储

简称为链栈。优点：便于多个栈共享存储空间和提高其效率，且不存在栈满上溢情况，多为单链表实现，并且所有操作都在规定在表头进行，下面就来示范一种不带头结点的：

 二、队列

 

1.定义

 一种操作受限的线性表，只允许在表的一端进行插入，另一端进行删除。

特性：先进先出（FIFO）

队头（front）：允许删除的一端，又成队首

队尾（rear）：允许插入一端

空队列：不含任何元素的空表。

2.基本操作

 3.队列的顺序存储

 

 上图分别为空队，5个元素入队，出队一次，和出队三次（从左到右）

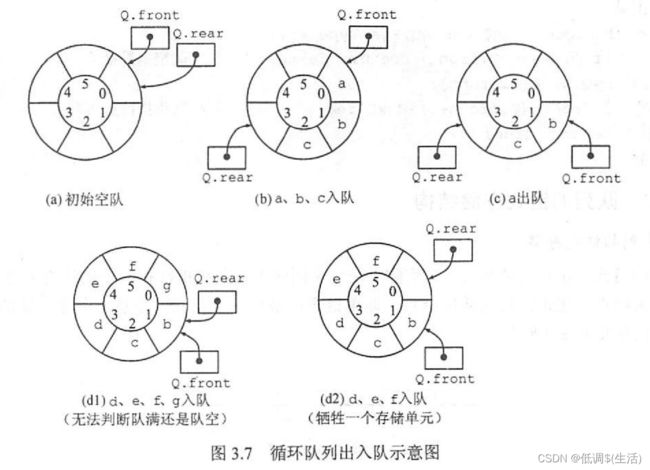
循环队列

原理

用除法取余运算来实现

 为了区分队空和队满，有三种处理方式：

1.牺牲一个单元来区分队空和队满

队满条件：（Q.rear+1）%MaxSize==Q.front

队空条件：Q.front==Q.rear

队列中元素个数：（Q.rear-Q.front+MaxSize）%MaxSize

2.类型中增设表示元素个数的数据成员。这样队空的条件为Q.size==0,队满为Q.size==MaxSize

3.增设tag数据成员。

tag等于0时，若因删除导致Q.front==Q.rear，则为队空。

tag等于1时，若因插入导致Q.front==Q.rear，则为队满。

循环队列基本操作

初始化
void InitQuene(SqQuene &Q){
    Q.rear=Q.front=0;
}

判空
bool isEmpty(SqQuene Q){
    if(Q.rear==Q.front)
        return true;
    else
        return false;
}
入队
bool EnQuene(SqQuene &Q,ElemType x){
    if((Q.rear+1)%MaxSize==Q.front)
        return false;//队满则报错
    Q.data[Q.rear]=x;
    Q.rear=(Q.rear+1)%MaxSize;
        return true;
}
出队
bool DeQuene(SqQuene &Q,ElemType &x){
    if(Q.rear==Q.front)
        return false;
    x=Q.data[Q.front];
    Q.front=(Q.front+1)%MaxSize;
        return true;
}

4.队列的链式存储结构

简称 链队列。实际上是一个同时带有队头指针和队尾指针的单链表。

 

存储类型如上。

由上述资料得出，我们推荐使用带头结点的单链表来表示队列。

基本操作

 5.双端队列

允许两端都进行入队和出队操作，逻辑结构仍为线性结构。分别有前端和后端。

下面是受限的情况

 三、数组

 1.定义

n个相同数据类型的数据元素构成的有限序列，每个元素的序号成为下标，下标的取值范围成为维界。

数组是线性表的推广，一维数组可视为线性表，二维数组可视为其元素也是定长线性表的线性表。数组一旦被定义，其维数和维界就不再改变。

 对于多维数组，有两种映射方式：按行优先和按列优先。

2.特殊矩阵的压缩存储

 1.对称矩阵 2.三角矩阵 3.对角矩阵 4.稀疏矩阵

这里描述太多了，基本数学中咱都学过，就不再多加描述了。