剑指 Offer 41. 数据流中的中位数-Python题解
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
示例 1:
输入:
[“MedianFinder”,“addNum”,“addNum”,“findMedian”,“addNum”,“findMedian”]
[[],[1],[2],[],[3],[]]
输出:[null,null,null,1.50000,null,2.00000]
示例 2:
输入:
[“MedianFinder”,“addNum”,“findMedian”,“addNum”,“findMedian”]
[[],[2],[],[3],[]]
输出:[null,null,2.00000,null,2.50000]
限制:
最多会对 addNum、findMedia进行 50000 次调用。
class MedianFinder:
def __init__(self):
"""
initialize your data structure here.
"""
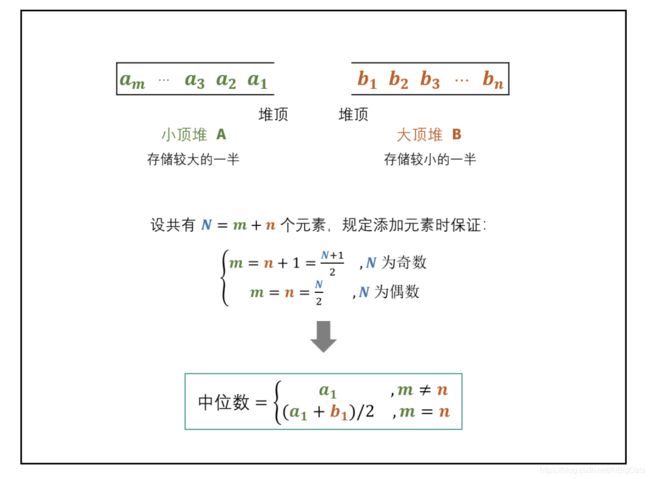
# 我们将数据流分成两大部分,后半部分a,前半部分b
# 如果len(a)==len(b),则b中最大的值加上a中最小值和的平均就为我们要求的中值
# 如果 len(a)!=len(b),说明是奇数,我们固定a组的个数比b组多,则中值就为a组的最小值
# a中存储数据流后半部分较大的值,heaqp存储这组的值,堆顶就是最小值,
self.a_data = []
# b中存储数据流的前部分,我们要得到这部分的最大值,
# 正常需要大顶堆,python中已实现的只有小顶堆,则这部分存储实际值的反数就好
self.b_data = []
def size(self, data):
return len(data)
# 获取当前堆中最小的数
def get(self, data):
if len(data) > 0:
return data[0]
# 弹出堆中最小的数字
def pop(self, data):
return heapq.heappop(data)
def push(self, data,item):
heapq.heappush(data, item)
def addNum(self, num: int) -> None:
if self.size(self.a_data) == self.size(self.b_data):
# 我们先往b组添加数字,然后b中的最大值放到a组存储
self.push(self.b_data, -num)
# b_data是大顶堆,弹出的值就是最大值,因为是从小顶堆通过取反得到的,则弹出的值要取反才是最大值
b_max_num = -self.pop(self.b_data)
# 将这个值加入a组中
self.push(self.a_data, b_max_num)
else:
# 同理,如果两组中成员的个数不相等,则一定是b组成员的个数少,那么先push到a组
self.push(self.a_data, num)
# 再把a组最小值拿出来,放到b组
a_smallest = self.pop(self.a_data)
# 放到b组要取反哦
self.push(self.b_data, -a_smallest)
def findMedian(self) -> float:
# 如果len(a)==len(b),a组最小值+b组最大值相加求平均,就是中位数
if self.size(self.a_data) == 0 and self.size(self.b_data) == 0:
return None
if self.size(self.a_data) == self.size(self.b_data) :
# b组成员要取反才是b组的最大值哦
return (self.get(self.a_data) - self.get(self.b_data)) / 2
# 如果是奇数,我们的规则是a组成员的个数是比b组多一个的
else:
return self.get(self.a_data)
# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()