李宏毅2020机器学习课堂笔记---semi_supervised Learning

Semi-Supervised Learning(半监督学习)

1、introduction

在现实生活中，我们的数据有被标记的也有没有标记的。当我们的数据都是被标记的时候，就符合监督学习的场景。

那么对于半监督学习来说，我们的数据一部分是被标记的，另一部分是没有标记的。一般来说，当我们的数据集 unlabel 的数据远大于 label的数据时，我们就要进行半监督学习。

半监督学习又可以分为下面两种方法：

• transductive learning(直推学习)：unlabeled data is the testing data

即，把testing data当做无标签的training data使用，适用于事先已经知道testing data的情况(一些比赛的时候)

值得注意的是，这种方法使用的仅仅是testing data的feature，而不是label，因此不会出现“直接对testing data做训练而产生cheating的效果

• inductive Learning（归纳学习）：unlabeled data is not the testing data

即，不把testing data的feature拿去给机器训练，适用于事先并不知道testing data的情况(更普遍的情况)

为什么要使用半监督学习？

实际上我们从来不缺data，只是缺有label的data，就像你可以拍很多照片，但它们一开始都是没有标签的。但是对这些数据进行标记又要付出昂贵的代价。在日常生活中，人类也都在进行半监督学习。

那么半监督学习有效果嘛？

半监督学习是基于一种假设的，半监督的学习效果的好坏完全看假设是否合理。因此假设是否合理显得至关重要。

2、Semi-supervised Learning for Generative Model

在生成模型的假设下，以高斯分布为例。

讲完了直观上的解释，接下来进行具体推导(假设做二元分类)：

• 先随机初始化一组参数：$\theta =\{P(C_1),P(C_2),u^1,u^2,\Sigma \}$

• step1：利用初始model计算每一笔unlabeled data $x^u$属于class 1的概率$P_{\theta }(C_1|x^u)$

• step2：update model

如果不考虑unlabeled data，则先验概率显然为属于class1的样本点数$N_1$/总的样本点数$N$，即$P(C_1)=\frac{N_1}{N}$

而考虑unlabeled data时，分子还要加上所有unlabeled data属于class 1的概率和，此时它们被看作小数，可以理解为按照概率一部分属于$C_1$，一部分属于$C_2$
$$P(C_1)=\frac{N_1+{\sum }_{x^u}P(C_1|x^u)}{N}$$
同理，对于均值，原先的mean $u_1=\frac{1}{N_1}\sum _{x^r\in C_1}{x}^r$加上根据概率对$x^u$求和再归一化的结果即可
$$u_1=\frac{1}{N_1}\sum _{x^r\in C_1}{x}^r+\frac{1}{{\sum }_{x^u}P(C_1|x^u)}\sum _{x^u}P(C_1|x^u)x^u$$
剩余的参数同理，接下来就有了一组新的参数${\theta }^{\prime }$，于是回到step1->step2->step1循环

• 理论上该方法保证是可以收敛的，而一开始给$\theta$的初始值会影响收敛的结果，类似gradient descent

• 上述的step1就是EM algorithm里的E，step2则是M

以上的推导基于的基本思想是，把unlabeled data $x^u$看成是可以划分的，一部分属于$C_1$，一部分属于$C_2$，此时它的概率$P_{\theta }(x^u)=P_{\theta }(x^u|C_1)P(C_1)+P_{\theta }(x^u|C_2)P(C_2)$，也就是$C_1$的先验概率乘上$C_1$这个class产生$x^u$的概率+$C_2$的先验概率乘上$C_2$这个class产生$x^u$的概率

实际上我们在利用极大似然函数更新参数的时候，就利用了该拆分的结果：
$$logL(\theta )=\sum _{x^r}log{P}_{\theta }(x^r)+\sum _{x^u}log{P}_{\theta }(x^u)$$

3、Low-density Separation Assumption：非黑即白

基于的假设是Low-density separation,也就是类与类之间的交界处 几乎没有数据的分布。

low-density separation最具代表性也最简单的方法是self training

• 先从labeled data去训练一个model $f^{\ast }$，训练方式没有限制
• 然后用该$f^{\ast }$去对unlabeled data打上label，$y^u=f^{\ast }(x^u)$，也叫作pseudo label(伪标签)
• 从unlabeled data中拿出一些data加到 labeled data里，至于data的选取需要你自己设计算法来挑选
• 回头再去训练$f^{\ast }$，循环即可

注：该方法对Regression是不适用的，这里我的理解是，本身用我定义好的模型进行预测，拿回去再去训练是没有什么影响的。

self-training 方法类似与上面假设的生成模型，区别在于，self-training的方法对标签是hard label（你觉得大概率上class 1 ，那他就是class 1。不需要给其他类别一点可能，类似于专情男），生成模型方法打标签的方式是soft label（分别对类别进行了可能性的分配，像极了渣男），对比之下，在network中，专情男的结果一定会优于渣男的结果。

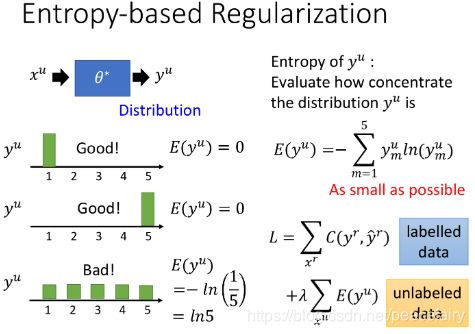
low-density separation的方法二：Entropy-based Regularization

该方法是low-density separation的进阶版，你可能会觉得hard label这种直接强制性打标签的方式有些太武断了，而entropy-based regularization则做了相应的改进：$y^u=f_{{\theta }^{\ast }}^{\ast }(x^u)$，其中$y^u$是一个概率分布(distribution)

由于我们不知道unlabeled data $x^u$的label到底是什么，但如果通过entropy-based regularization得到的分布集中在某个class上的话，那这个model就是好的，而如果分布是比较分散的，那这个model就是不好的，如下图所示：

我们的目标是在labeled data上分类要正确，在unlabeled data上，output的entropy要越小越好。改善方法就是要修改loss function：

• 可以发现该式长得很像regularization，这也就是entropy regularization的名称由来

Semi-supervised SVM

4、Smoothness Assumption：近朱者赤，近墨者黑

粗糙的定义是相似的x具有相同的$\hat{y}$
精确的定义是：

• x的分布是不平均的

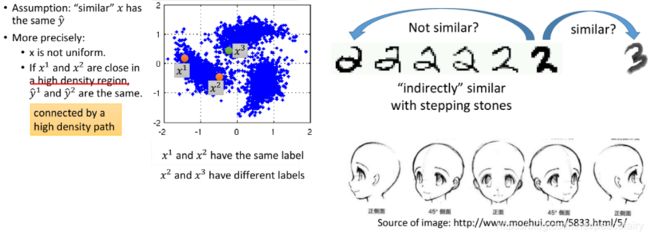
• 如果$x^1$和$x^2$在一个high density region上很接近的话，那么${\hat{y}}^1$和${\hat{y}}^2$就是相同的，也就是这两个点可以在样本点高密度集中分布的区域块中有一条可连接的路径，即 connected by a high density path。

举例来说：

解决方法-cluster and then label

先把data分成几个cluster，划分class之后再拿去训练，但这种方法不一定会得到好的结果，因为它的假设是你可以把同一个class的样本点cluster在一起，而这其实是没那么容易的.

Graph-based Approach

如何定性的表示Graph？（一般就直觉+经验）老师列举了几种方式
如何定量的表示Graph？

定量的使用方式是定义label的smoothness，下图中，edge上的数字是weight，$x^i$表达data，$y^i$表示data的label，计算smoothness的方式为：
$$S=\frac{1}{2}\sum _{i,j}{w}_{i,j}(y^i-y^j{)}^2$$
我们期望smooth的值越小越好
根据 数学上的某个定理又可以进一步化简公式：
$$S=\frac{1}{2}\sum _{i,j}{w}_{i,j}(y^i-y^j{)}^2=y^{T}Ly$$其中L为(R+U)×(R+U) matrix，成为Graph Laplacian， 定义为$L=D-W$

• W：把data point两两之间weight的关系建成matrix，代表了$x^i$与$x^j$之间的weight值
• D：把W的每一个row上的值加起来放在该行对应的diagonal上即可，比如5=2+3,3=2+1,…
  对$S=y^{T}Ly$来说，y是label，是neural network的output，取决于neural network的parameters，因此要在原来仅针对labeled data的loss function中加上这一项，得到：
  $$L=\sum _{x^r}C(y^r,{\hat{y}}^r)+\lambda S$$
  $\lambda S$实际上也是一个regularization term。

具体训练的时候，不一定只局限于neural network的output要smooth，可以对中间任意一个hidden layer加上smooth的限制

5、Better Representation：去芜存菁，化繁为简

我们观察到的世界是比较复杂的，而在它的背后其实是有一些比较简单的东西，在操控着这个复杂的世界，所以只要你能够看透这个世界的假象，直指它的核心的话，就可以让training变得比较容易

举一个例子，在神雕侠侣中，杨过要在三招之内剪掉樊一翁的胡子，虽然胡子的变化是比较复杂的，但头的变化是有限的，杨过看透了这一件事情就可以把胡子剪掉。在这个例子中，樊一翁的胡子就是original representation，而他的头就是你要找的better representation

具体细节可参考 非监督学习中的分析。