逻辑设计法:数字电路在PLC编程中的体现
2021.11.07
——
参考文献
[1]罗庚兴.浅谈用PLC改造继电器控制系统的方法.煤矿机械,2006,27(7):159-161.
[2]清华大学电子学教研组. 数字电子技术基础简明教程[M]. 第三版. 北京:高等教育出版社, 2006.
1逻辑代数
在提到一般教科书都会记载,但实际上较少使用的逻辑设计法之前,有必要先回顾一下贯穿整本数电课本的逻辑代数(Logic
Algebra)这一知识点。
逻辑代数,或称布尔代数(Bool Algebra),是按一定的逻辑关系进行运算的代数,其基本逻辑运算有与(AND)、或(OR)、非(NOT)。
- 与运算: Y = A ⋅ B Y=A·B Y=A⋅B
- 或运算: Y = A + B Y=A+B Y=A+B
- 非运算: Y = A ‾ Y=\overline{A} Y=A
在逻辑代数中,使用英文字母表示变量,称为逻辑变量,其取值为0或1;上式1-3被称为逻辑表达式,式中A、B称为输入逻辑变量,Y称为输出逻辑变量;字母上面无反号的称为原变量,有反号的称为反变量。
当Y=F(A,B,…)时,称Y是A、B、…的逻辑函数。
逻辑函数在各个变量之间存在互相制约关系,则称之为约束,该逻辑函数称为有约束的逻辑函数,这些变量称为一组有约束的变量。
2 PLC的逻辑设计法
2.1电路->逻辑代数
逻辑代数是分析和综合开关电路的重要数学工具,因此又称为开关代数。
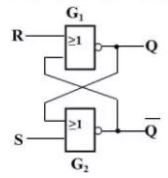
下图所示的三类电路,可用于反应与、或、非三种基本逻辑关系:

根据继电器电路图推导逻辑函数表达式,遵循原则见下:
- 电器开关的逻辑函数以线圈作为输出逻辑变量,以触点作为输入逻辑变量;
- 线圈得电为 “1”,线圈断电为“0“;
- 常开触点用原变量表示,常闭触点用反变量表示 ;触点动作为“1”,不动作为“0”;
- 时间继电器的线圈与其延时动作触点的逻辑状态不一致 ,并且时间继电器的触点有4种状态(延时断开、延时闭合、瞬动断开、瞬动闭合),需要作特殊处理 。
PLC梯形图(称作继电器梯形图)程序编程原理与开关电路设计原理相同,因此方法相同,可以参照前文方法来设计程序。
以使用继电器为核心的起保停电路为例:
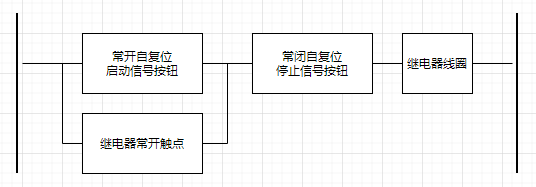
扩展到一般对象,其逻辑代数表示为:
F k = ( X 开 + K ) ⋅ X ‾ 关 F_k=(X_开+K)·\overline{X}_关 Fk=(X开+K)⋅X关
X 开 X_开 X开——控制对象开启信号
X 关 X_关 X关——控制对象关断信号
K K K——输出对象的常开触点
在实际应用中, X 开 X_开 X开和 X 关 X_关 X关会带有约束条件,防止启停信号误动作的影响,保障系统可靠性:

其逻辑函数为:
F k = ( X 开 ⋅ X 开约 + K ) ⋅ ( X ‾ 关 + X ‾ 关约 F_k=(X_开·X_{开约}+K)·(\overline{X}_关+\overline{X}_{关约} Fk=(X开⋅X开约+K)⋅(X关+X关约)
2.2逻辑代数->梯形图
对于PLC梯形图编程,在没有约束条件下,典型输出控制对象的基本逻辑函数可表示为:
F k = ( X 开 + K ) ⋅ X ‾ 关 F_k=(X_开+K)·\overline{X}_关 Fk=(X开+K)⋅X关
X 开 X_开 X开——启动条件
X ‾ 关 \overline{X}_关 X关——关断条件
K K K——控制对象的当前状态
F K F_K FK——控制对象的下一个状态值
约束条件下,典型输出控制对象的基本逻辑函数可表示为:
F k = ( X 开 ⋅ X 开约 + K ) ⋅ ( X ‾ 关 + X ‾ 关约 ) F_k=(X_开·X_{开约}+K)·(\overline{X}_关+\overline{X}_{关约}) Fk=(X开⋅X开约+K)⋅(X关+X关约)
其对应的PLC程序如下:

逻辑设计法的基本使用方法即为:把各种已知信号带入上式中,写出控制对象的逻辑函数,再根据逻辑函数,结合一般设计原则,编写PLC程序。
3实例一则
现在尝试用逻辑设计法解一道题,这是我从网络上搜索到的,不过我学习PLC时也按经验法写过类似的题目。题目和原链接相比有改动,倒不是原题做不来,是我写完了以后发现题目和我写的有差别( ̄▽ ̄)"。
某企业承担了小车往返控制系统的设计任务。要求小车在A、B、C三点之间来回移动(A、B、C三点在一条路线上),一个周期的工作过程为:原位在A点,按下启动按钮后,小车从A点前进至B点,碰到行程开关SQ1后返回至A点,碰到行程开关SQ2后又前进,经过B点不停直接运行到C点,碰到行程开关SQ3返回至A点,完成一个周期后循环。按下停止按钮时,小车即刻停止。

因为牵扯到动作时序,用步进梯形图会容易很多,否则逻辑会比较复杂,但为了体现逻辑代数的优越性,现在我们反其道而行之,并使用逻辑设计法解这道题。
基本逻辑函数见下:
Y 前进 = ( X 开 + Y 前进 + X A ⋅ Y 后退下降沿 ) ⋅ ( X B ‾ ⋅ X B 约 ‾ + X C ‾ ⋅ X C 约 ) ⋅ X 关 ‾ Y_{前进}=(X_开+Y_{前进}+X_A·Y_{后退下降沿})·(\overline {X_B}·\overline {X_{B约}}+\overline {X_C}·X_{C约})·\overline {X_关} Y前进=(X开+Y前进+XA⋅Y后退下降沿)⋅(XB⋅XB约+XC⋅XC约)⋅X关
Y 后退 = ( Y 前进下降沿 ⋅ ( X B + X C ) + Y 后退 ) ⋅ X A ‾ ⋅ X 关 ‾ Y_{后退}=(Y_{前进下降沿}·(X_B+X_C)+Y_{后退})·\overline {X_A}·\overline {X_关} Y后退=(Y前进下降沿⋅(XB+XC)+Y后退)⋅XA⋅X关
上述逻辑函数的格式为 启动条件 ⋅ 完成条件 ⋅ 停止条件 启动条件·完成条件·停止条件 启动条件⋅完成条件⋅停止条件
为了防止同时输出前进和后退信号,加入了XB约束条件 X B 约 X_{B约} XB约和XC约束条件 X C 约 X_{C约} XC约, X B 约 X_{B约} XB约为真的条件是本循环已抵达B点; X C 约 X_{C约} XC约为真的条件是本循环已抵达A点和B点;循环结束后会对约束条件进行复位。
4利用逻辑表达式实现梯形图程序对数字电路的模拟
4.1对1位数值比较器的模拟
实际上我们可以根据逻辑表达式来编写梯形图程序,模拟一类数字电路。
例如以1位数值比较器为例,其逻辑表达式为:
L i = A i B ‾ i L_i=A_i\overline B_i Li=AiBi
G i = A ‾ i B ‾ i + A i B i G_i=\overline A_i\overline B_i+A_iB_i Gi=AiBi+AiBi
M i = A ‾ i B i M_i=\overline A_i B_i Mi=AiBi
根据上述逻辑表达式可编写如下梯形图程序:

其真值表如下:
| A i A_i Ai | B i B_i Bi | L i L_i Li | G i G_i Gi | M i M_i Mi |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
同1位数值比较器的真值表一致。
4.2从数字电路演化到功能块
实际上梯形图中的一些功能块即是数字电路的程序化体现,例如RS触发器(复位/置位触发器):
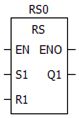
在数字电路中,触发器是用于接收、保存和输出二进制数字信号和两状态逻辑信号的单元单路,其重要概念有现态和次态。
- 现态:触发器接收输入信号之前的状态,用 Q n Q^n Qn表示。
- 次态:触发器接收输入信号之后的状态,用 Q n + 1 Q^{n+1} Qn+1表示。次态既取决于输入信号,也取决于现态(保持特性)。
R R R、 S S S是信号输入端,表示低电平有效
Q Q Q、 Q ‾ \overline{Q} Q是两个互补的信号输出端,表示触发器状态
当电路无输入信号( R R R= S S S=1)时,有两个状态:
0状态: Q Q Q=0、 Q ‾ \overline{Q} Q=1
1状态: Q Q Q=1、 Q ‾ \overline{Q} Q=0
当 R R R=1、 S S S=0时,触发器将变成1状态,因此习惯上把 S S S端称为置位端;
当 R R R=0、 S S S=1时,触发器将变成0状态,因此习惯上把 R R R端称为复位端;
不允许 R R R= S S S=1,此即为约束条件。
特性方程用于描述基本RS触发器次态输出 Q n + 1 Q^{n+1} Qn+1与现态 Q n Q^{n} Qn和输入 R R R、 S S S之间的函数关系。
RS基本触发器的特性方程为:
{ Q n + 1 = S + R ‾ ⋅ Q n R S = 0 约束条件 \begin{cases} Q^{n+1}=S+\overline{R}·Q^{n}\\ RS=0~~~~~~~约束条件 \end{cases} {Qn+1=S+R⋅QnRS=0 约束条件