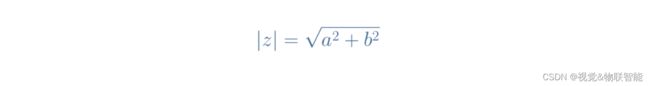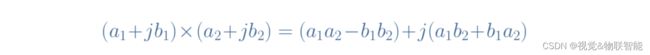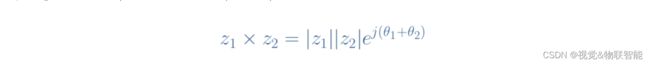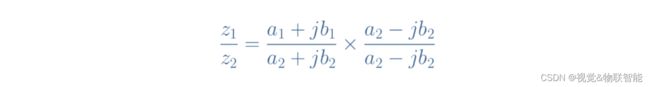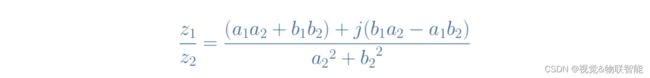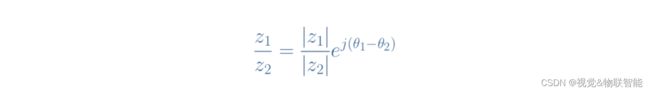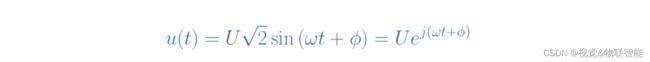【电路笔记】-电路中的复数与相量(Phasor)

电路中的复数与相量(Phasor)

复数是一种重要的数学工具，广泛应用于包括电子学在内的许多物理领域。 这个概念可能看起来很奇怪，但它们的操作很简单，而且效率很高。

在第一部分中，介绍了有关复数的一般概念，以便熟悉它们的表示形式。 接下来的第二部分将列举一些与复数相关的最重要的定义。 在定义了一些关键概念之后，第三部分将更详细地讨论它们的计算规则。 最后，我们将了解为什么它们被用于电子领域并作为一种有效的工具简化计算。

1、概述

本节从纯数学的角度介绍复数及其关联的集合。 复数集记为$\mathbb{C}$，它是我们熟悉的通常实数集的扩展。 因此，实数包含在复数中。

定义复数的起点是虚数单位 $i$，在电子学中也记为 $j$，以避免与电流混淆。 这个数字的定义如$j^2=-1$，在一些国家或机构中，也可能遇到$j=\sqrt{-}1$的表示法。

实数可以在沿直线的一维空间中表示，而复数可以在称为复平面的二维空间中表示。 该结构如下图1所示：

图1：复平面上复数的表示

我们先来谈谈复平面，它由两个轴组成，可以表示任何复数。 横轴是实数集，纵轴是虚轴。

如图1所示，复数 $z$ 可以用表示坐标的两个实数 $a$ 和 $b$ 来描述，也可以用距离 $|z|$ 来描述。 和角度$\theta$。 描述 $z$ 的第一个选项称为代数形式，在以下公式1中定义：

公式1：复数z的代数形式

强调一些特殊案例很有趣。 如果$b=0$，$z=a$，表示复数化简为实数。 若$a=0$，$z=jb$，则$z$称为纯虚数。

定义$z$的第二种方法称为极坐标或指数形式。 在给出这种形式的表达式之前，我们需要了解$|z|$由什么组成。 和$\theta$。 值$|z|$，也称为模，是复平面原点与复数之间的距离。 它由毕达哥拉斯定理定义，如公式2所示：

公式2：模块的定义

$\theta$称为参数，定义实轴和复数之间的角度。 除非 $a=0$ 且 $b=0$ 或 $a<0$ 且 $b=0$，否则始终可以使用以下公式计算参数：

公式3：参数定义

使用欧拉公式，复数$z$的极坐标描述由距离和角度给出，并满足以下公式：

公式4：复数z的极坐标形式

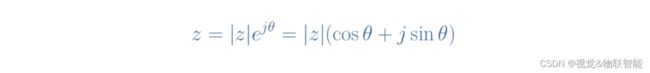
2、复数定义

许多定义都与复数相关。

复杂代数中经常使用两个简单的运算符：Re 和 Im。 假设一个复数 $z=a+jb$，实部运算符Re 定义为 $Re(z)=a$，虚部运算符定义为 $Im(z)=b$。 另一种更简单的确定复数参数$\theta$的方法（条件是 $Re(z)>0$）由下式给出：$\theta =\arctan (Im(z)/Re(z))$。

复共轭是另一个重要的定义，广泛应用于复代数中。 复数$z$的复共轭记为$z^{\ast }$，并且实部相同但虚部相反：如果$z=a+jb$，则 $z^{\ast }=a-jb$。 以指数形式，如果$z=|z|e^{j\theta }$，则$z^{\ast }=|z|e^{-j\theta }$。 复数共轭可以建立许多关系，但最重要的一个是 $z\times z^{\ast }=|z{|}^2$。

在复平面中，共轭运算转化为相对于实轴 的对称性：

图2：共轭变换

有趣的是，如果 $Im(z)=0$，则 $z=z^{\ast }$ ：实数的复共轭是该数本身。 而且，共轭运算是可逆的：$(z^{\ast }{)}^{\ast }=z$。

3、复数计算规则

两个复数 $z1=a1+jb1$ 和 $z2=a2+jb2$ 的加（或减）在于分别考虑实部和虚部：

公式5：两个复数相加

例如，对于实数，复数的乘法具有分配性，在重新组合实部和虚部后如公式6 所示：

公式6：使用指数形式的乘法

然而，使用代数形式进行复数除法运算比使用实数进行除法运算更加复杂。 让我们考虑一下之前定义的两个复数 $z_1$ 和 $z_2$。 执行除法的技巧是将复数分母转换为实数分母。 为此，我们将分子和分母都乘以分母复共轭，如下所示：

通过实现如前所示的乘法，我们现在得到一个可以除以实分母的复数分子：

公式8：两个复数相除
下面假设：$z_1=2+4j$ 和 $z_2=3+j$，复数除法计算$z_1 / z_2$如下：

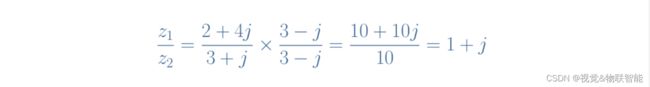
这个结果也可以写成指数形式 $z_1/z_2=\sqrt{2}{e}^{j\pi /4}$。

正如我们强调的乘法运算，除法可以使用指数形式更轻松地完成：

公式9：复数除法指数形式

可以用相同的例子来验证公式9。 首先，我们需要计算 $z_1$ 和 $z_2$ 的模块和参数：

• $|z_1|=\sqrt{2^2+4^2}=\sqrt{20}$
• ${\theta }_1=Arg(z_1)=\arctan (4/2)=\arctan (2)$
• $|z_2|=\sqrt{3^2+1^2}=\sqrt{10}$
• ${\theta }_2=Arg(z_2)=\arctan (1/3)$

模的除法给出$|z_1|/|z_2|=\sqrt{2}$，除法的参数是$\arctan (2)-\arctan (1/3)=\pi /4$。 因此，除法的结果是 $\sqrt{2}{e}^{j\pi /4}$，证实了我们之前使用代数形式计算的结果。

4、电子领域的复数

任何周期性信号（例如电流或电压）都可以使用复数来书写，从而简化了符号和相关计算：

公式10：电压的复杂表示法

复数表示法还用于描述电容器和电感器的阻抗及其相移。 确实可以证明：

• $Z_C=1/C\omega$ 和${\varphi }_C=-\pi /2$
• $Z_L=L\omega$ 和${\Phi }_L=+\pi /2$

由于 $e^{\pm j\pi /2}=\pm j$，复数阻抗 $Z^{\ast }$ 可以同时考虑相移以及电容器和电感器的电阻：

• $Z_C^{\ast }=-j/C\omega$
• $Z_L^{\ast }=jL\omega$

我们可以将一个简单的 RLC 电路与其相关的复数阻抗 $Z_R$、$Z_L$ 和 $Z_C$ 串联作为示例。 因此，总复阻抗为：$Z_{RLC}=Z_R+Z_L+Z_C=R+j(L\omega -1/C\omega )$。

该阻抗的虚部称为电抗，记为 X，在此示例中，$X_{RLC}=L\omega -1/C\omega$。 我们可以区分三种情况来描述电路的行为：

• $X=0$ 表示电路是纯电阻性的：它充当电阻并遵循欧姆定律
• $X<0$ 电路是电容性的：它充当电容并且倾向于对电压的任何变化产生抵抗。
• $X>0$ 电路是电感性的：它充当电感并引起对电流的任何变化的反对。

RLC电路的总阻抗由$Z_{RLC}$的模给出：$|Z_{RLC}|=\sqrt{R^2+X_{RLC}^2}$。

电压和电流之间的相移由 $Z_{RLC}$ 的参数给出，即：$Arg(Z_{RLC})=\arctan (X_{RLC}/R)$。

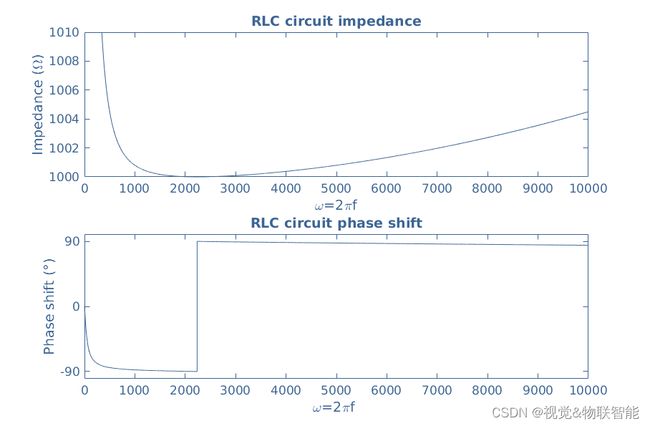
阻抗和相移都取决于信号的频率。 这种演变可以使用MatLab® 来表示（下面图3所示），其中选择的组件包括 $R=1k\Omega$、$L=10mH$$C=20\mu F$。

图3：RLC串联电路的阻抗和相移

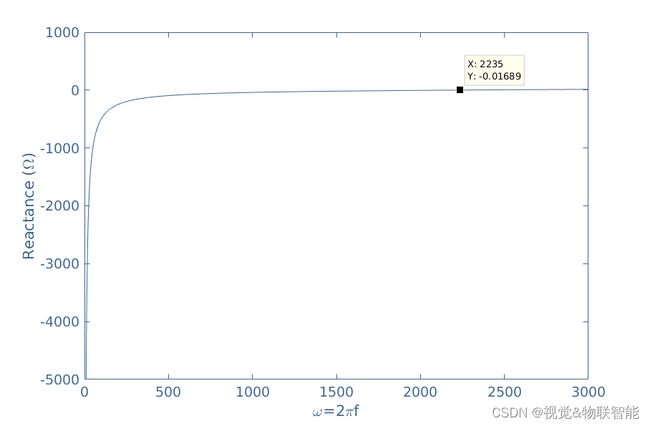
我们可以注意到，首先该电路是电容性的，因为它呈现负相移并在一定频率值后变为电感性。 此结论可以通过绘制图4中的电抗来验证，其中显示负值和正值之间的转变发生在相同的特定频率下：

图4：RLC串联电路的电抗

这个特定频率$f_0=2235/2\pi =356Hz$称为电路的谐振频率，满足$X=0$。 在我们的示例中，$X_{RLC}=0\Rightarrow \omega 0=1/\sqrt{L}C=2235$，图 4 中突出显示的值证实了这一点。

5、总结

• 复数已经出现了近 500 年，并且是由高斯或柯西等一些最杰出的数学家建立的。 从那时起，它们被用于许多科学领域，例如电子学，并且它是一个强大的工具。
• 在第一部分中，介绍了复数的概念。 复数集可以看作一个平面，其中每个数字都可以通过坐标（代数形式）或距离和角度（指数形式）来定义。 复数具有可以解某些通常实数无法解的方程的性质，例如方程 x^2=-1$。 第二节介绍了一些更重要的概念，例如共轭变换。
• 计算规则在第三部分中介绍。 我们已经看到，加法、减法和乘法与实数和复数非常相似。 然而，除法运算需要更多步骤，涉及共轭变换的使用。
• 最后，我们看到了如何在电子学中使用复数来描述周期性信号、阻抗并确定频率相关状态下的电路行为。