代码随想录day37｜贪心收尾｜738.单调递增的数字｜714. 买卖股票的最佳时机含手续费｜968.监控二叉树｜贪心总结｜Golang

代码随想录day37

今天结束后，剩下DP大头了

目录

代码随想录day37

738.单调递增的数字

714. 买卖股票的最佳时机含手续费

968.监控二叉树

贪心算法总结

---

738.单调递增的数字

贪心算法

        题目要求小于等于N的最大单调递增的整数，那么拿一个两位的数字来举例。

        例如：98，一旦出现strNum[i - 1] > strNum[i]的情况（非单调递增），首先想让strNum[i - 1]--，然后strNum[i]给为9，这样这个整数就是89，即小于98的最大的单调递增整数。

        这一点如果想清楚了，这道题就好办了。

        局部最优：遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]--，然后strNum[i]给为9，可以保证这两位变成最大单调递增整数。

        全局最优：得到小于等于N的最大单调递增的整数。

        但这里局部最优推出全局最优，还需要其他条件，即遍历顺序，和标记从哪一位开始统一改成9。此时是从前向后遍历还是从后向前遍历呢？

        从前向后遍历的话，遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]减一，但此时如果strNum[i - 1]减一了，可能又小于strNum[i - 2]。

        这么说有点抽象，举个例子，数字：332，从前向后遍历的话，那么就把变成了329，此时2又小于了第一位的3了，真正的结果应该是299。

        所以从前后向遍历会改变已经遍历过的结果！

        那么从后向前遍历，就可以重复利用上次比较得出的结果了，从后向前遍历332的数值变化为：332 -> 329 -> 299

        确定了遍历顺序之后，那么此时局部最优就可以推出全局，找不出反例，试试贪心。

Go代码如下：

func monotoneIncreasingDigits(N int) int {
    s := strconv.Itoa(N)//将数字转为字符串，方便使用下标
    ss := []byte(s)//将字符串转为byte数组，方便更改。
    n := len(ss)
    if n <= 1 {
        return N
    }
    for i:=n-1 ; i>0; i-- {
        if ss[i-1] > ss[i] {//前一个大于后一位,前一位减1，后面的全部置为9
            ss[i-1] -= 1
            for j := i ; j < n; j++ {//后面的全部置为9
                ss[j] = '9'
            }
        } 
    }
    res, _ := strconv.Atoi(string(ss))
    return res 
}

714. 买卖股票的最佳时机含手续费

贪心算法

在贪心算法：122.买卖股票的最佳时机II

中使用贪心策略不用关心具体什么时候买卖，只要收集每天的正利润，最后稳稳的就是最大利润了。

        而本题有了手续费，就要关系什么时候买卖了，因为计算所获得利润，需要考虑买卖利润可能不足以手续费的情况。

        如果使用贪心策略，就是最低值买，最高值（如果算上手续费还盈利）就卖。

此时无非就是要找到两个点，买入日期，和卖出日期。

• 买入日期：其实很好想，遇到更低点就记录一下。
• 卖出日期：这个就不好算了，但也没有必要算出准确的卖出日期，只要当前价格大于（最低价格+手续费），就可以收获利润，至于准确的卖出日期，就是连续收获利润区间里的最后一天（并不需要计算是具体哪一天）。

所以我们在做收获利润操作的时候其实有三种情况：

• 情况一：收获利润的这一天并不是收获利润区间里的最后一天（不是真正的卖出，相当于持有股票），所以后面要继续收获利润。
• 情况二：前一天是收获利润区间里的最后一天（相当于真正的卖出了），今天要重新记录最小价格了。
• 情况三：不作操作，保持原有状态（买入，卖出，不买不卖）

贪心算法Go代码如下：

 

func maxProfit(prices []int, fee int) int {
    buy := prices[0] + fee 
    profit := 0
    for i:=1;i buy { // 该出手了
            profit += prices[i] - buy
            buy = prices[i]     // 留一手
        }
    }
    return profit
}

        本题贪心的思路其实是比较难的，动态规划才是常规做法，但也算是给大家拓展一下思路，感受一下贪心的魅力。

        后期我们在讲解 股票问题系列的时候，会用动规的方式把股票问题穿个线

968.监控二叉树

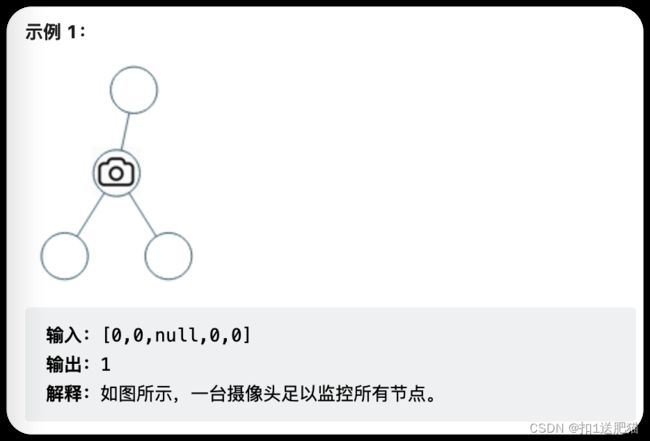
        给定一个二叉树，我们在树的节点上安装摄像头。节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。计算监控树的所有节点所需的最小摄像头数量。

 

思路

        这道题目首先要想，如何放置，才能让摄像头最小的呢？

        从题目中示例，其实可以得到启发，我们发现题目示例中的摄像头都没有放在叶子节点上！

        这是很重要的一个线索，摄像头可以覆盖上中下三层，如果把摄像头放在叶子节点上，就浪费的一层的覆盖。

        所以把摄像头放在叶子节点的父节点位置，才能充分利用摄像头的覆盖面积。

        那么有同学可能问了，为什么不从头结点开始看起呢，为啥要从叶子节点看呢？

        因为头结点放不放摄像头也就省下一个摄像头， 叶子节点放不放摄像头省下了的摄像头数量是指数阶别的。

        所以我们要从下往上看，局部最优：让叶子节点的父节点安摄像头，所用摄像头最少，整体最优：全部摄像头数量所用最少！

        局部最优推出全局最优，找不出反例，那么就按照贪心来！

        此时，大体思路就是从低到上，先给叶子节点父节点放个摄像头，然后隔两个节点放一个摄像头，直至到二叉树头结点。

此时这道题目还有两个难点：

1. 二叉树的遍历
2. 如何隔两个节点放一个摄像头

# 确定遍历顺序

        在二叉树中如何从低向上推导呢？

        可以使用后序遍历也就是左右中的顺序，这样就可以在回溯的过程中从下到上进行推导了。

后序遍历代码如下：

func traversal(root *TreeNode) {

    // 空节点，该节点有覆盖
    if (终止条件) return 

    left := traversal(cur.left);    // 左
    right := traversal(cur.right);  // 右

    逻辑处理                            // 中
    return 
}

        注意在以上代码中我们取了左孩子的返回值，右孩子的返回值，即left 和 right， 以后推导中间节点的状态

如何隔两个节点放一个摄像头

        此时需要状态转移的公式，大家不要和动态的状态转移公式混到一起，本题状态转移没有择优的过程，就是单纯的状态转移！来看看这个状态应该如何转移，先来看看每个节点可能有几种状态：

有如下三种：

• 该节点无覆盖
• 本节点有摄像头
• 本节点有覆盖

我们分别有三个数字来表示：

• 0：该节点无覆盖
• 1：本节点有摄像头
• 2：本节点有覆盖

大家应该找不出第四个节点的状态了。

        一些同学可能会想有没有第四种状态：本节点无摄像头，其实无摄像头就是 无覆盖 或者 有覆盖的状态，所以一共还是三个状态。

        因为在遍历树的过程中，就会遇到空节点，那么问题来了，空节点究竟是哪一种状态呢？ 空节点表示无覆盖？ 表示有摄像头？还是有覆盖呢？

        回归本质，为了让摄像头数量最少，我们要尽量让叶子节点的父节点安装摄像头，这样才能摄像头的数量最少。

        那么空节点不能是无覆盖的状态，这样叶子节点就要放摄像头了，空节点也不能是有摄像头的状态，这样叶子节点的父节点就没有必要放摄像头了，而是可以把摄像头放在叶子节点的爷爷节点上。

        所以空节点的状态只能是有覆盖，这样就可以在叶子节点的父节点放摄像头了

接下来就是递推关系。

        那么递归的终止条件应该是遇到了空节点，此时应该返回2（有覆盖），原因上面已经解释过了。

代码如下：

// 空节点，该节点有覆盖
if cur == NULL) {
    return 2
}

递归的函数，以及终止条件已经确定了，再来看单层逻辑处理。

主要有如下四类情况：

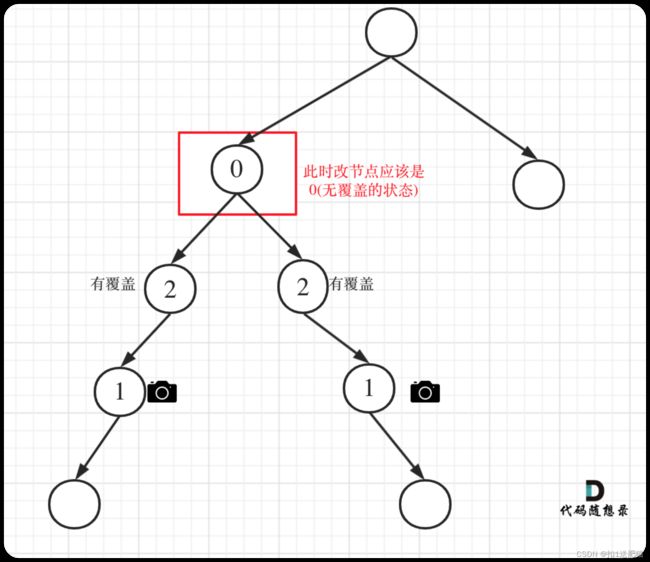
• 情况1：左右节点都有覆盖

左孩子有覆盖，右孩子有覆盖，那么此时中间节点应该就是无覆盖的状态了。

如图：

 代码如下：

// 左右节点都有覆盖
if (left == 2 && right == 2) return 0;

• 情况2：左右节点至少有一个无覆盖的情况

如果是以下情况，则中间节点（父节点）应该放摄像头：

left == 0 && right == 0 左右节点无覆盖

left == 1 && right == 0 左节点有摄像头，右节点无覆盖

left == 0 && right == 1 左节点有无覆盖，右节点摄像头

left == 0 && right == 2 左节点无覆盖，右节点覆盖

left == 2 && right == 0 左节点覆盖，右节点无覆盖

        这个不难理解，毕竟有一个孩子没有覆盖，父节点就应该放摄像头。此时摄像头的数量要加一，并且return 1，代表中间节点放摄像头。

代码如下：

if (left == 0 || right == 0) {
    result++;
    return 1;
}

• 情况3：左右节点至少有一个有摄像头

        如果是以下情况，其实就是 左右孩子节点有一个有摄像头了，那么其父节点就应该是2（覆盖的状态）

        left == 1 && right == 2 左节点有摄像头，右节点有覆盖

        left == 2 && right == 1 左节点有覆盖，右节点有摄像头

        left == 1 && right == 1 左右节点都有摄像头

代码如下：

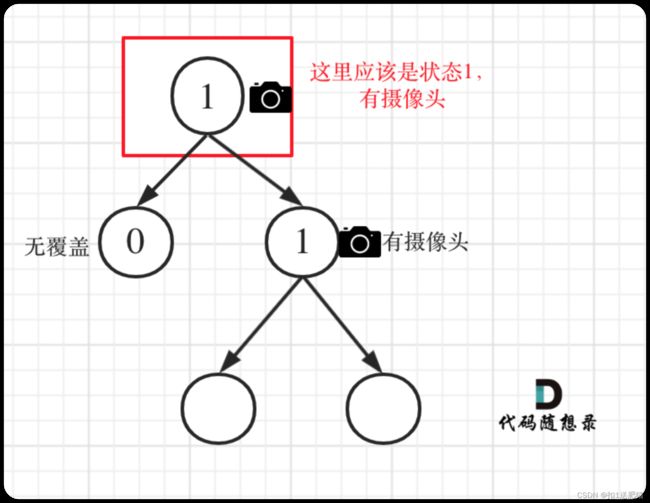
if (left == 1 || right == 1) return 2;

        从这个代码中，可以看出，如果left == 1, right == 0 怎么办？其实这种条件在情况2中已经判断过了，如图：

这种情况也是大多数同学容易迷惑的情况。

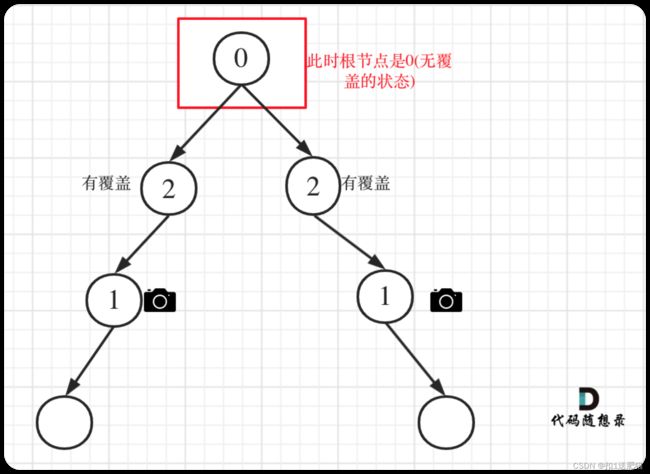
•情况4：头结点没有覆盖

以上都处理完了，递归结束之后，可能头结点 还有一个无覆盖的情况，如图：

 所以递归结束之后，还要判断根节点，如果没有覆盖，result++，代码如下：

int minCameraCover(TreeNode* root) {
    result = 0;
    if (traversal(root) == 0) { // root 无覆盖
        result++;
    }
    return result;
}

以上四种情况我们分析完了，代码也差不多了，整体代码如下：

（以下我的代码注释很详细，为了把情况说清楚，特别把每种情况列出来。）

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

var res int

func minCameraCover(root *TreeNode) int {

    res = 0
    if dfs(root) == 1 {
        // 如果最顶端的元素没有被安装，也没有被监视
        // 那么这个节点需要安装一个摄像头
        res ++
    }
    return res;
}

// 1未被监视, 2安装摄像头
// 一个c一个v骗骗自己罢了

func dfs(root *TreeNode) int {

    // 最后一个节点不关心
    if root == nil {
        return 0
    }

    left := dfs(root.Left)
    right := dfs(root.Right)

    // 如果子节点没有被监视
    if left == 1 || right == 1 {
        // 安装摄像头
        res++
        return 2
    }

    // 如果子节点安装摄像头
    if left == 2 || right == 2 {
        // 标记被监视
        return 3
    }
    return 1
}

贪心算法总结

没有总结。多刷题，最后一道还是不懂的。再学学吧。