算法-前缀和数组、差分数组
目录
前缀和
1,前缀和 + 二分查找
2,前缀和 + 哈希
3, 前缀和 + 差分
4,前缀和二维数组
5,最大区间和
差分数组
1,leetcode370 区间加法(直接考察的差分数组技巧):
2,leetcode航班预订系统
3,1094. 拼车
Leetcode]253. 会议室 II(数组/堆)
前缀和
见:力扣
前缀和指一个数组的某下标之前的所有数组元素的和(包含其自身),前缀和是一种重要的预处理,能够降低算法的时间复杂度。
用途:
前缀和主要适用的场景是原始数组不会被修改的情况下,频繁查询某个区间的累加和。
给定数组:nums[n] = {a1, a2, ...., an-1};共n个元素
前缀和数组:preSum[n + 1] = {0, a1, a1 + a2, ...., a1+..+an-1};
// 构造前缀和
vector preSum(n + 1);
preSum[0] = 0;
for (int i = 0; i < n; i++) {
preSum[i + 1] = preSum[i] + nums[i];
} 可推导出2个变换公式:
(1)nums的[i, j]区间元素的和(包括i, j)等于:preSum[j + 1] - preSum[i],(以nums的下标维度,遍历范围:[0, numsSize))
特例:nums[i]([i, i]区间元素的和)等于preSum[i + 1] - preSum[i]
(2)preSum[i] 记录给定数组nums中 [0, i - 1] 区间的元素和(其中 i = 1, 2, ..., preSumSize-1)。(以preSum的下标维度, 遍历范围:[1, preSumSize))
1,前缀和 + 二分查找
1712. 将数组分成三个子数组的方案数
//前缀和+二分:提示连续子数组和--想到前缀和, 且非负--前缀和单调升序--想到二分
// 思路
// 遍历前缀和数组, 设遍历中的下标i为left和mid的闭区间边界(边界1),此时[i + 1, preSumSize -2]区间内查找划分mid和right的边界(边界2),使得满足leftSum <= midSum <= rightSum条件。
// 边界2最小值为lowerIdx, 边界2最大值为upperIdx。即边界2闭区间[lowerIdx, upperIdx]内的所有值都满足本轮在边界1的情况下使得leftSum <= midSum <= rightSum成立。
// (1)先寻找lowerIdx:在[i + 1, preSumSize - 1)区间内,只需找满足midSum=(preSum[边界2] - preSum[i]) >= leftSum条
// 件(即找target = 2 * leftSum)的lower_bound就是边界2最小值。
// (2)再寻找upperIdx:在[i + 1, preSumSize - 1)区间内,只需找满足rightSum=(preSum[preSumSize-1] - preSum[边界2]) >= midSum=(preSum[边界2] - preSum[i])条
// 件(即找target = preSum[i] + (preSum[preSumSize-1] - preSum[i]) / 2, 即midSum和rightSum的平均值)的upper_bound就是边界2最大值
// (3)对lowerIdx和upperIdx进行有效区间判定:按照midSum>=leftSum寻找到lowerIdx,又按照rightSum>=midSum寻找到midSum,因此当upperIdx >= lowerIdx时,
// 就得到了边界2有效的闭区间范围[lowerIdx, upperIdx]使得leftSum <= midSum <= rightSum
/*
{1, 2, 2, 2, 5, 0}
i 0 1 2 3 4 5 6
{0, 1, 3|, 5, 7, 12, 12}
i:2
当用i=2分出leftSum,那么在[i + 1, preSumSize - 1)区间找target,而求midSum时是始终用preSum[mid] - leftSum求得,求rightSum时始终用preSum[preSumSize - 1] - leftSum求得
leftIdx, target = 2 * leftSum
rightIdx,target = leftSum + (preSum[preSumSize - 1] - leftSum) / 2
leftIdx:4
{0, 1, 3|, 5, 7|, 12, 12|} // 在[i + 1, preSumSize - 1)区间找target=2*3=6的lowerbound, leftIdx = lowerboundIdx
[0, 1][1, 3][3, 5]
{1, 2}{2, 2}{5, 0}
3-0=3 7-3=4 12-7=5
rightIdx:4
{0, 1, 3|, 5, 7|, 12, 12} // 在[i + 1, preSumSize - 1)即{5, 7, 12}区间找target=3 + (12-3)/2 = 7的upperbound, rightIdx = upperboundIdx - 1
[0, 1][1, 3][3, 5]
{1, 2}{2, 2}{5, 0}
3 4 5
i 0 1 2 3 4 5 6
{0, 1|, 3, 5, 7, 12, 12}
i:1
leftIdx:2
{0, 1|, 3|,5, 7, 12, 12|} // 在[i + 1, preSumSize - 1)区间找target=2*1=2的lowerbound, leftIdx = lowerboundIdx
1 2 12-3=9
rightIdx:3
{0, 1|, 3, 5|, 7, 12, 12} // 在[i + 1, preSumSize - 1)区间找target=1 + (12-1)/2 = 6的upperbound, rightIdx = upperboundIdx - 1
1 5-1=4 12-5 = 7
*/二分模板见:二分搜索模板_u011764940的博客-CSDN博客
class Solution {
public:
int waysToSplit(vector& a) {
int aSize = a.size();
vector preSum(aSize + 1);
for (int i = 0; i < aSize; i++) {
preSum[i + 1] = preSum[i] + a[i];
}
long long res = 0;
int preSumSize = preSum.size();
// 因为是直接用preSum[i]标识nums的和,因此用preSum索引[1, n]遍历
for (int i = 1; i < preSumSize - 2; i ++) { // 剪枝:left和mid的分界点不能大于等于在preSumSize - 2这样分不出left/mid/right三段
int leftSum = preSum[i]; // a数组[0, i - 1)的区间和
if (leftSum * 3 > preSum[preSumSize - 1]) { // 剪枝
break;
}
// 调标准库:228ms
// int leftIdx = lower_bound(preSum.begin() + i, preSum.end() - 1, 2 * leftSum) - preSum.begin(); // lower_bound是找大于等于target,满足leftIdx的左闭
// int rightIdx = upper_bound(preSum.begin() + i, preSum.end() - 1, leftSum + (preSum[aSize] - leftSum) / 2) - preSum.begin() - 1; // upper_bound是找大于target,是右开,因此减1后得到右闭且减1会使midSum更小于rightSum
// 调手写:160ms
int leftIdx = LowerBound(preSum, i + 1, preSumSize - 1, 2 * leftSum);
int rightIdx = UpperBound(preSum, i + 1, preSumSize - 1, leftSum + (preSum[preSumSize - 1] - leftSum) / 2) - 1;
// leftIdx = max(i + 1, leftIdx); // 可略,因为本身就是在i + 1起始点开始找的,LowerBound返回值可能范围[i+1, preSumSize-1]
// rightIdx = min(preSumSize - 2, rightIdx); // 可略, UpperBound返回的是大于target的idx(可能的范围是[i+1, preSumSize-1]), 已经减去1了(可能的范围是[i, preSumSize-2])
if (rightIdx >= leftIdx) {
res += (rightIdx - leftIdx + 1);
}
}
return res % int(1e9 + 7);
}
private:
// 入参搜索范围[left, right)及结果均与std::lower_bound相同
int LowerBound(const vector &nums, int left, int right, int target)
{
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
right = mid;
} else if (nums[mid] > target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
}
}
return left;
}
// 入参搜索范围[left, right)及结果均与std::upper_bound相同
int UpperBound(const vector &nums, int left, int right, int target)
{
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
}
}
return left;
}
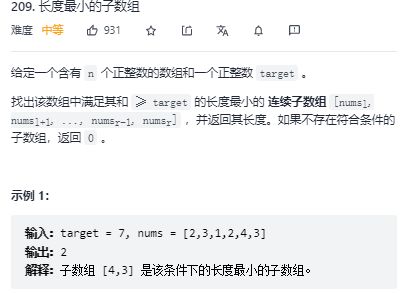
}; 209. 长度最小的子数组 --(可以用滑动窗口,也可以用前缀和+二分)
算法滑动窗口_u011764940的博客-CSDN博客
法1:滑动窗口
class Solution {
public:
int minSubArrayLen(int s, vector& nums) {
int sum = 0;
int left = 0;
int right = 0;
int result = nums.size();
while (right < nums.size()) {
sum += nums[right];
right++;
while (sum >= s) {
result = min(result, right - left);
sum -= nums[left];
left++;
}
}
return result;
}
}; 法2:前缀和 + 二分
因为这道题保证了数组中每个元素都为正,所以前缀和一定是递增的,这一点保证了二分的正确性。如果题目没有说明数组中每个元素都为正,这里就不能使用二分来查找这个位置了。
class Solution {
public:
int minSubArrayLen(int s, vector& nums) {
int n = nums.size();
if (n == 0) {
return 0;
}
int ans = INT_MAX;
vector sums(n + 1, 0);
for (int i = 1; i <= n; i++) {
sums[i] = sums[i - 1] + nums[i - 1];
}
for (int i = 1; i <= n; i++) {
int target = s + sums[i - 1];
auto bound = lower_bound(sums.begin(), sums.end(), target);
if (bound != sums.end()) {
ans = min(ans, static_cast((bound - sums.begin()) - (i - 1)));
}
}
return ans == INT_MAX ? 0 : ans;
}
}; 2,前缀和 + 哈希
560. 和为 K 的子数组
// (1)遍历前缀和数组的过程中,在i之前找是否存在值(preSum[i] - target),若存在说明有连续数组和为target
// (2)因此,用map记录到前缀和出现的个数。且map的内容不能在遍历之前初始化,只能在遍历到i,在map中查找过(preSum[i] - target)后才能把当前key:preSum[i]的添加到map中prefixMap[prefix[i]]++;。只有这样才能是在preSum数组i之前找是否存在值(preSum[i] - target)。
另外:要先记录mp[0]=1,表示前缀和为0的有1个。
// 思路
// 1, 连续子数组问题, 考虑采用滑动窗口或前缀和
// 2,因为数组元素可以为负数,若采用滑动窗口算法,保证不了滑动窗口右边界时窗口内sum值递增,滑动左边界时sum值递减,导致不断地滑动
// 右边界和左边界。会退化为O(n平方)时间复杂度。
// 3, 需要采用前缀和来达到O(N). sum[i, j] = preSum[j + 1] - preSum[i], i,j闭区间
// 初始化要加入 {0,1} 这对映射,这是为啥呢,因为解题思路是遍历数组中的数字,
// 用 sum 来记录到当前位置的累加和,建立 HashMap 的目的是为了可以快速的查找 sum-k 是否存在,
// 即是否有连续子数组的和为 sum-k,如果存在的话,那么和为k的子数组一定也存在,这样当 sum 刚好为k的时候,
// 那么数组从起始到当前位置的这段子数组的和就是k,满足题意,如果 HashMap 中事先没有 m[0] 项的话,
// 这个符合题意的结果就无法累加到结果 res 中,这就是初始化的用途。
class Solution {
public:
int subarraySum(vector& nums, int k) {
int res = 0;
int sum = 0;
int n = nums.size();
unordered_map mp{{0, 1}};
for (int i = 0; i < n; ++i) {
sum += nums[i];
if (mp.find(sum - k) != mp.end()) {
res += mp[sum - k];
}
mp[sum]++;
}
return res;
}
};
class Solution1 {
public:
int subarraySum(vector& nums, int k) {
int count = 0;
int n = nums.size();
vector prefix(n + 1, 0);
for(int i = 0; i < n; i++){
prefix[i + 1] = prefix[i] + nums[i];
}
unordered_map prefixMap;
prefixMap[0] = 1;
for(int i = 1; i <= n; i++){
if(prefixMap.find(prefix[i] - k) != prefixMap.end()){
count += prefixMap[prefix[i] - k];
}
prefixMap[prefix[i]]++;
}
return count;
}
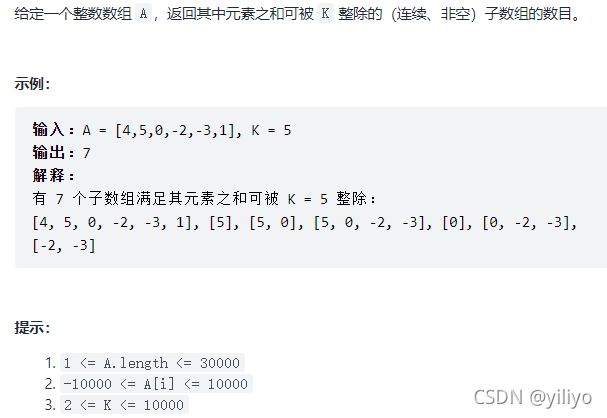
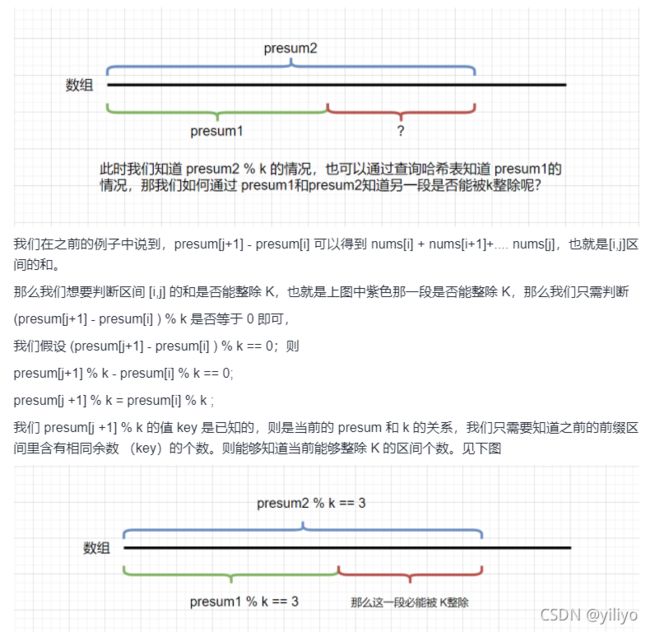
}; 974. 和可被 K 整除的子数组
思路:同余定理
class Solution {
public:
int subarraysDivByK(vector& nums, int k) {
unordered_map record = {{0, 1}};
int sum = 0, ans = 0;
for (int elem: nums) {
sum += elem;
// 注意 C++ 取模的特殊性,当被除数为负数时取模结果为负数,需要纠正
int modulus = (sum % k + k) % k;
if (record.count(modulus)) {
ans += record[modulus];
}
++record[modulus];
}
return ans;
}
};
3, 前缀和 + 差分
1094. 拼车
思路及算法:(差分数组 -> 前缀和数组) + 哈希
考虑利用 差分数组 简化问题
这里为了描述清楚,引入两个数组(当然也可以直接累加在 diff 数组上):
diff 数组表示每个位置 i 与前一个位置乘客的差值---差分数组
cap 数组表示每个位置 i 有多少乘客 ----对差分数组计算出前缀和数组
此时遍历 trips 数组就可以完成对 diff 数组的初始化,
diff[t[1]] += t[0];
diff[t[2]] -= t[0];
之后利用前缀和得到 cap 数组即可。
由于只要最后一个上车点满足最大乘客容量,后续下车只会使得人数更少,所以判断到 最大上车点 maxId 就可以了
如果中间出现了容量不足的情况,直接返回 false
class Solution {
public boolean carPooling(int[][] trips, int capacity) {
int N = 1010, maxId = 0;
int[] diff = new int[N]; // 这里就是差分框架里的构建diff数组,只不过原始输入都是0,那么diff
// 数组也是全0,不需要差分框架构造函数里的for循环求diff了
int[] cap = new int[N];
for (int[] t : trips) { // 这里就是差分框架里的increase过程,区间内数组增减
maxId = Math.max(maxId, t[1]);
diff[t[1]] += t[0];
diff[t[2]] -= t[0];
}
if (diff[0] > capacity) return false;
cap[0] = diff[0];
for (int i = 1; i <= maxId; i++) { // 这里就是差分框架的result。用到了前缀和计算。对diff求
// 前缀和
cap[i] = cap[i - 1] + diff[i];
if (cap[i] > capacity) return false;
}
return true;
}
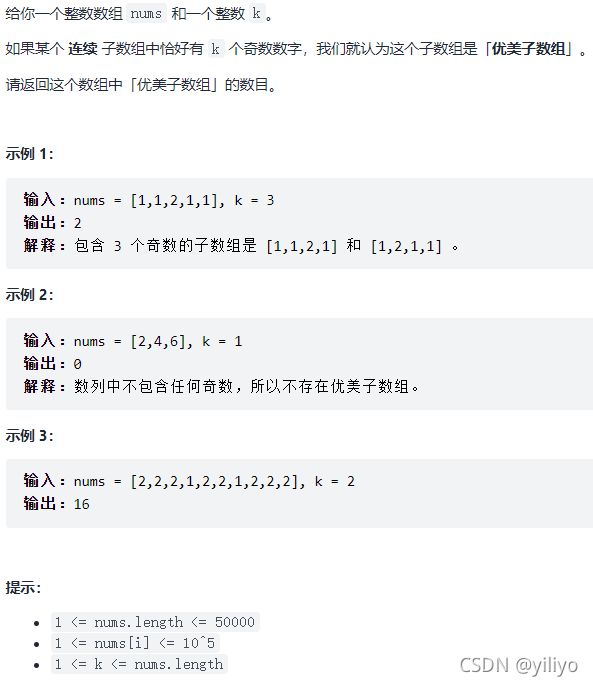
}1248. 统计「优美子数组」
注:(1)解法1和解法2都没有显示的用到差分数组,即没有先遍历原数组[1,1,2,1,1]根据各元素是否奇数构建出[1,10,1,1]的差分数组,然后遍历差分数组,对差分数组计算前缀和数组。而是一遍遍历根据原数组元素是否是奇数,直接累加到前缀和数组上。 (2)都是用到了前缀和 + 哈希的解法。
解法1:隐式的利用前缀和,不构建前缀和数组,而是以一个odd累加值来表示到i为止的奇数的sum值。
class Solution {
vector cnt;
public:
int numberOfSubarrays(vector& nums, int k) {
int n = (int)nums.size();
cnt.resize(n + 1, 0);
int odd = 0, ans = 0;
cnt[0] = 1;
for (int i = 0; i < n; ++i) {
odd += nums[i] & 1;
ans += odd >= k ? cnt[odd - k] : 0;
cnt[odd] += 1;
}
return ans;
}
};
解法2:显示的利用前缀和数组
class Solution {
public:
// 前缀和 + hash:228ms, 18.28%
int numberOfSubarrays(vector& nums, int k) {
// 构造preSum;
vector preSum(nums.size() + 1, 0);
for (int i = 0; i < nums.size(); i++) {
preSum[i + 1] = (nums[i] & 1) == 1 ? preSum[i] + 1 : preSum[i];
}
// 前缀和+hash:求连续子数组和为k
unordered_map mp{{0, 1}};
int res = 0;
for (int i = 1; i < preSum.size(); i++) {
int rem = preSum[i] - k;
if (mp.count(rem)) {
res += mp[rem];
}
mp[preSum[i]]++;
}
return res;
}
}; 4,前缀和二维数组
计算公式:
二维前缀和 S[i][j] = S[i-1][j] + S[i][j-1] – S[i-1][j-1] + A[i][j]
子矩阵(r1, c1)到(r2, c2)的和为:S[r2][c2] – S[r1-1][c2] – S[r2][c1-1] + S[r1-1][c1-1]
法1:用一维前缀和数组解
// 法1:每行是原始数组每行的前缀和,遍历(row1,row2)行,累加每行的区域和
class NumMatrix {
public:
NumMatrix(vector>& matrix) {
matrixPreSum = vector>(matrix.size(), vector(matrix[0].size() + 1, 0));
for (int i = 0; i < matrix.size(); i++) {
for (int j = 0; j < matrix[0].size(); j++) {
matrixPreSum[i][j + 1] = matrixPreSum[i][j] + matrix[i][j];
}
}
}
int sumRegion(int row1, int col1, int row2, int col2) {
int res = 0;
if (row1 > row2 || col1 > col2) {
return 0;
}
for (int i = row1; i <= row2; i++) {
res += (matrixPreSum[i][col2 + 1] - matrixPreSum[i][col1]);
}
return res;
}
private:
vector> matrixPreSum;
}; 法2:用二维前缀和数组解。
前缀和数组记录的是(x,y)到原点(0,0)矩阵面积。即/ (0, 0, x, y)矩阵的和。
// 法2:计算每个点(x,y)到(0,0)围成区域的前缀和。最终要求的(row1, col1, row2, col2)区域和是区域(0,0,row2,col2)减去(0,0,row2,col1)、(0,0,row1,col2) 加上 (0,0,row1,col1)。
class NumMatrix {
public:
NumMatrix(vector>& matrix) {
matrixPreSum = vector>(matrix.size() + 1, vector(matrix[0].size() + 1, 0));
// vector> vec = {{3,0,1,4,2},
// {5,6,3,2,1},
// {1,2,0,1,5},
// {4,1,0,1,7},
// {1,0,3,0,5}};
// vector> vec1 = {{0,0,0,0,0,0},
// {0,3,0,1,4,2},
// {0,5,6,3,2,1},
// {0,1,2,0,1,5},
// {0,4,1,0,1,7},
// {0,1,0,3,0,5}};
for (int i = 1; i <= matrix.size(); i++) {
for (int j = 1; j <= matrix[0].size(); j++) {
matrixPreSum[i][j] = matrix[i - 1][j - 1] + matrixPreSum[i][j - 1] + matrixPreSum[i - 1][j] -
matrixPreSum[i - 1][j - 1];
}
}
}
int sumRegion(int row1, int col1, int row2, int col2) {
int res = 0;
if (row1 > row2 || col1 > col2) {
return 0;
}
res = matrixPreSum[row2 + 1][col2 + 1] - matrixPreSum[row2 + 1][col1] - matrixPreSum[row1][col2 + 1] +
matrixPreSum[row1][col1];
return res;
}
private:
// (0, 0, x, y)矩阵的面积和
vector> matrixPreSum;
}; 5,最大区间和
方法:前缀和 + 贪心
思路:计算出前缀和数组。另用res和minpresum分别维护着最大区间和和到目前i索引为止最小前缀和。遍历数组(原始数组),用presum[i+1] - minpresum就可以得到一个对本i来说最大的一个区间和(因为minpresum是最小值),如果presum[i+1] - minpresum跟res比较比res大,则用presum[i+1] - minpresum更新res。接着判断presum[i+1]是否小于minpresum,若小于则用presum[i+1]更新minpresum。
题目:求数组中相同元素值组成的最大区间和,返回区间的起始和结束索引。
示例1:
输入:[1,2,3,2,3,4]
输出:[2,4]
示例2:
[4,6,7,4,-1,-3,4]
[0,3]
方法1:前缀和 + 按三个条件排序(可用vector
// 思路:s1:先记录前缀和; s2:遍历原数组边把相同值对应索引记录到map key的vector中,并内部遍历相同值索引vector计算出
// [idx1,idx2,sum1to2]记录到二维vector或优先队列
// 时间复杂度:O(N^2)
class solution {
public:
static bool cmp(vector& in1, vector& in2)
{
if (in1[2] == in2[2]) {
if (in2[0] < in1[0]) {
return true;
}
return in2[1] < in1[1];
}
return in1[2] < in2[2];
}
vector GetIndexList(vector &score)
{
vector result;
// 堆顶维护最终要求的结果, 维护大顶堆
priority_queue, vector>, decltype(cmp)*> priQue(cmp);
vector prefixSum(score.size() + 1, 0);
unordered_map> hashMap;
for (int i = 0; i < score.size(); i++) {
prefixSum[i + 1] = score[i] + prefixSum[i];
}
for (int i = 0; i < score.size(); i++) {
hashMap[score[i]].push_back(i);
if (hashMap[score[i]].size() == 1) {
continue;
}
vector& valIdxVec = hashMap[score[i]];
for (auto idx : valIdxVec) {
if (idx == i) {
continue;
}
priQue.push({idx, i, prefixSum[i + 1] - prefixSum[idx]}); // nums的[i, j]区间元素的和(包括i, j)等于:
// preSum[j + 1] - preSum[i], 以nums的下标维度
}
}
return {priQue.top()[0], priQue.top()[1]};
}
};
方法2:前缀和 + hashmap中始终维护相同key的最小前缀和及其索引(这样到下一个相同key时,直接减去map中维护的那个最小前缀和就得到最大区间前缀和)
思路:s1:先记录前缀和; s2:一遍遍历原数组,本次key对应的前缀和减去map中维护的相同key对应的最小前缀和得到最大区间和,比较并更新result,之后再更新map中这个key对应的最小前缀和
两个注意点:
(1)求区间和,用prefixSum[i + 1] - prefixSum[preMsg.idx]而不是prefixSum[i + 1] - preMsg.idxPrefixSum
(2)区间值相等时一定记得比较idx,若本区间的起始索引preMsg.idx比结果中idx小则更新(因为map维护了相同key的最小前缀和及相同前缀和时小索引,因此区间值相等,且起始索引preMsg.idx和result[0]也相等的情况,不需要更新结果集,就保证了区间结束索引小的在前)
// 时间复杂度:O(N)
class MinPrifixMsg {
public:
MinPrifixMsg(int i, int prefixSum) : idx(i), idxPrefixSum(prefixSum) {};
MinPrifixMsg() {};
int idx;
int idxPrefixSum;
bool operator<(const MinPrifixMsg& rMsg) {
if (idxPrefixSum == rMsg.idxPrefixSum) {
return idx < rMsg.idx;
} else {
return idxPrefixSum < rMsg.idxPrefixSum;
}
}
};
class solution1 {
public:
vector GetIndexList(vector &score)
{
vector result(2);
int maxRangeSum = INT_MIN;
vector prefixSum(score.size() + 1, 0);
for (int i = 0; i < score.size(); i++) {
prefixSum[i + 1] = score[i] + prefixSum[i];
}
unordered_map hashMap;
for (int i = 0; i < score.size(); i++) {
if (hashMap.count(score[i]) == 0) {
hashMap[score[i]] = MinPrifixMsg(i, prefixSum[i + 1]);
continue;
}
MinPrifixMsg& preMsg = hashMap[score[i]];
int rangeSum = prefixSum[i + 1] - prefixSum[preMsg.idx]; // (1)求区间和,用prefixSum[i + 1] - prefixSum[preMsg.idx]而不是prefixSum[i + 1] - preMsg.idxPrefixSum
if (rangeSum > maxRangeSum) {
maxRangeSum = rangeSum;
result[0] = preMsg.idx;
result[1] = i;
} else if (rangeSum == maxRangeSum && preMsg.idx < result[0]) { // (2) 区间值相等时一定记得比较idx,若本区间的起始索引preMsg.idx比结果中idx小则更新(因为map维护了相同key的最小前缀和及相同前缀和时小索引,因此区间值相等,且起始索引preMsg.idx和result[0]也相等的情况,不需要更新结果集,就保证了区间结束索引小的在前)
result[0] = preMsg.idx;
result[1] = i;
}
MinPrifixMsg curMsg(i, prefixSum[i + 1]);
if (curMsg < preMsg) {
preMsg.idx = curMsg.idx;
preMsg.idxPrefixSum = curMsg.idxPrefixSum;
}
}
return maxRangeSum == INT_MIN ? vector() : result;
}
}; 差分数组
摘自labuladong:小而美的算法技巧:差分数组 :: labuladong的算法小抄
差分,是一种和前缀和相对的策略。这种策略是,令![]() ,即相邻两数的差。
,即相邻两数的差。
差分数组定义
真实数组a = {a[1]、a[2]、…、a[n]} // 各点真实数据
差分数组df = {df[1]、df[2]、…、df[n]} // 各点数据的变更值
df[i] = a[i] - a[i-1] // 差分数组各点数据为真实数据的变更值
a[i] = df[1] + df[2] …+ df[i] // 差分数组的前缀和即为真实数组
a[i] = a[i-1] + df[i] // 真实数据也可以从上一点数据+变更值求出
差分算法解题模板(题目中给出的往往为数据变更点)
初始化差分数组:根据数据变更点构造差分数组,常用map
根据差分数组求原始数组:对差分数组求前缀和,求出的即为原始数组
根据原始数组判断结果
用途:
差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。
比如说,我给你输入一个数组 nums,然后又要求给区间 nums[2..6] 全部加 1,再给 nums[3..9] 全部减 3,再给 nums[0..4] 全部加 2,再给…
常规的思路很容易,你让我给区间 nums[i..j] 加上 val,那我就一个 for 循环给它们都加上呗,还能咋样?这种思路的时间复杂度是 O(N),由于这个场景下对 nums 的修改非常频繁,所以效率会很低下。
这里就需要差分数组的技巧,类似前缀和技巧构造的 prefix 数组,我们先对 nums 数组构造一个 diff 差分数组,diff[i] 就是 nums[i] 和 nums[i-1] 之差:
注:与前缀和数组的区别:
(1) 差分数组元素个数等于原数组元素个数,前缀和数组一般是(原数组元素个数+1)。
(2) 差分计算过程里是包含前缀和计算过程的,即第3步:计算result中,对diff数组做前缀和。差分是多出来第1步:用原数组计算出diff数组,第2步:闭区间增减值。而如果原数组元素值全零,那么差分的第1步也就可以省略,直接计算第2步和第3步,eg:leecode1094上面前缀和解法和下面差分解法。
int[] diff = new int[nums.length];
// 构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}通过这个 diff 差分数组是可以反推出原始数组 nums 的,代码逻辑如下:
int[] res = new int[diff.length];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}这样构造差分数组 diff,就可以快速进行区间增减的操作,如果你想对区间 nums[i..j] 的元素全部加 3,那么只需要让 diff[i] += 3,然后再让 diff[j+1] -= 3 即可:
原理很简单,回想 diff 数组反推 nums 数组的过程,diff[i] += 3 意味着给 nums[i..] 所有的元素都加了 3,然后 diff[j+1] -= 3 又意味着对于 nums[j+1..] 所有元素再减 3,那综合起来,是不是就是对 nums[i..j] 中的所有元素都加 3 了?
只要花费 O(1) 的时间修改 diff 数组,就相当于给 nums 的整个区间做了修改。多次修改 diff,然后通过 diff 数组反推,即可得到 nums 修改后的结果。
现在我们把差分数组抽象成一个类,包含 increment 方法和 result 方法:
注:原始数组作为构造函数的输入项。(若原始元素为全0,那么差分数组也为全0,那么经过所有的增减动作后,差分数组结果就是最终返回数组的结果)
// 差分数组工具类
class Difference {
// 差分数组
private int[] diff;
/* 输入一个初始数组,区间操作将在这个数组上进行 */
public Difference(int[] nums) {
assert nums.length > 0;
diff = new int[nums.length];
// 根据初始数组构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
/* 给闭区间 [i,j] 增加 val(可以是负数)*/
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
/* 返回结果数组 */
public int[] result() {
int[] res = new int[diff.length];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
}
这里注意一下 increment 方法中的 if 语句:
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}当 j+1 >= diff.length 时,说明是对 nums[i] 及以后的整个数组都进行修改,那么就不需要再给 diff 数组减 val 了。
题目:
1,leetcode370 区间加法(直接考察的差分数组技巧):
那么我们直接复用刚才实现的 Difference 类就能把这道题解决掉:
注:原始数组元素全0。
int[] getModifiedArray(int length, int[][] updates) {
// nums 初始化为全 0
int[] nums = new int[length];
// 构造差分解法
Difference df = new Difference(nums);
for (int[] update : updates) {
int i = update[0];
int j = update[1];
int val = update[2];
df.increment(i, j, val);
}
return df.result();
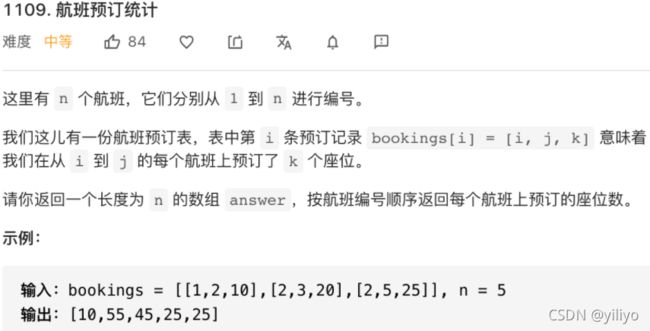
}2,leetcode航班预订系统
当然,实际的算法题可能需要我们对题目进行联想和抽象,不会这么直接地让你看出来要用差分数组技巧。
本题就是一个差分数组题:
给你输入一个长度为 n 的原始数组 nums,其中所有元素都是 0。再给你输入一个 bookings,里面是若干三元组 (i,j,k),每个三元组的含义就是要求你给 nums 数组的闭区间 [i-1,j-1] 中所有元素都加上 k。请你返回最后的 nums 数组是多少?
int[] corpFlightBookings(int[][] bookings, int n) {
// nums 初始化为全 0
int[] nums = new int[n];
// 构造差分解法
Difference df = new Difference(nums);
for (int[] booking : bookings) {
// 注意转成数组索引要减一哦
int i = booking[0] - 1;
int j = booking[1] - 1;
int val = booking[2];
// 对区间 nums[i..j] 增加 val
df.increment(i, j, val);
}
// 返回最终的结果数组
return df.result();
}3,1094. 拼车
题目描述见前缀和。
相信你已经能够联想到差分数组技巧了:trips[i] 代表着一组区间操作,旅客的上车和下车就相当于数组的区间加减;只要结果数组中的元素都小于 capacity,就说明可以不超载运输所有旅客。
但问题是,差分数组的长度(车站的个数)应该是多少呢?题目没有直接给,但给出了数据取值范围:0 <= trips[i][1] < trips[i][2] <= 1000
车站个数最多为 1000,那么我们的差分数组长度可以直接设置为 1001:
boolean carPooling(int[][] trips, int capacity) {
// 最多有 1000 个车站
int[] nums = new int[1001];
// 构造差分解法
Difference df = new Difference(nums);
for (int[] trip : trips) {
// 乘客数量
int val = trip[0];
// 第 trip[1] 站乘客上车
int i = trip[1];
// 第 trip[2] 站乘客已经下车,
// 即乘客在车上的区间是 [trip[1], trip[2] - 1]
int j = trip[2] - 1;
// 进行区间操作
df.increment(i, j, val);
}
int[] res = df.result();
// 客车自始至终都不应该超载
for (int i = 0; i < res.length; i++) {
if (capacity < res[i]) {
return false;
}
}
return true;
}Leetcode]253. 会议室 II(数组/堆)
// 方法5:差分
// 思路:各区间内会议室都加1。注意:因为要知道差分数组大小,输入区间end值可能非常大,内存消耗会大
class Solution4 {
public:
int minMeetingRooms(vector>& intervals) {
// 求差分数组大小
int maxEnd = (*max_element(intervals.begin(), intervals.end(), [](vector& in1, vector& in2){
return in1[1] < in2[1];
}))[1];
// 创建差分数组
vector diff;
diff.resize(maxEnd);
// 根据区间更新差分数组
for (auto& ele : intervals) {
diff[ele[0]] += 1;
if (ele[1] == maxEnd) {
continue;
}
diff[ele[1]] -= 1;
}
int res = 0;
// 对差分数组求前缀和
int sum = 0;
for (auto ele : diff) {
sum += ele;
res = max(res, sum);
}
return res;
}
}; /*
方法1:优先队列 + 贪心
思路:先按会议结束时间排序。再遍历数组,优先队列中动态存放会议结束时间,若遍历的当前元素,循环比较会议起始值大于等于优先队列顶元素值,说明当前会议与这个堆顶元素会议不重叠,pop出堆顶。结束之后,说明当前会议与当前堆中对早结束的会议及其以后的会议都会重叠,因此用result = max(result, (int)pq.size());记录最大重叠会议数。
类似题目:lc452. Minimum Number of Arrows to Burst Balloons(贪心)
class Solution {
public:
int minMeetingRooms(vector>& intervals)
{
int result = 1;
sort(intervals.begin(), intervals.end(), [](vector& in1, vector& in2){
return in1[1] < in2[1];
});
multiset pq; // 小根堆
pq.insert(intervals[0][1]);
for (int i = 1; i < intervals.size(); i++) {
while (!pq.empty() && intervals[i][0] >= *pq.begin()) {
pq.erase(pq.begin());
}
pq.insert(intervals[i][1]);
result = max(result, (int)pq.size());
}
return result;
}
}; /*
方法4:优先队列:
再来一看一种使用最小堆来解题的方法,这种方法先把所有的时间区间按照起始时间排序,然后新建一个最小堆,开始遍历时间区间,如果堆不为空,且首元素小于等于当前区间的起始时间,去掉堆中的首元素,把当前区间的结束时间压入堆,由于最小堆是小的在前面,那么假如首元素小于等于起始时间,说明上一个会议已经结束,可以用该会议室开始下一个会议了,所以不用分配新的会议室,遍历完成后堆中元素的个数即为需要的会议室的个数,参见代码如下;
注:和方法一的思路区别:堆中仍放会议的结束时间,下一会议起始时间只需要和堆顶元素比较,若小于等于堆顶,说明堆顶会议已结束,就可以用该已结束的会议室开始当前遍历到的会议。而不需要while来比较当前遍历到的会议起始时间与堆顶的下一会议比较。
本方法就是常规思路,按会议起始时间排序,优先队列中记录会议结束时间,若要开始一个会议,则先看下本会议开始时间是否大于等于堆顶的时间,若大于说明可以继续复用堆顶的那个会议室,而不用分配新的会议室。
*/
class Solution3 {
public:
int minMeetingRooms(vector>& intervals) {
sort(intervals.begin(), intervals.end(), [](const vector& a, const vector& b){ return a[0] < b[0]; });
priority_queue, greater> q;
for (auto interval : intervals) {
if (!q.empty() && q.top() <= interval[0]) q.pop();
q.push(interval[1]);
}
return q.size();
}
}; /*
方法2:差分数组的思想:对于起始时间,映射值自增1,对于结束时间,映射值自减1。只是用map来代替了diff数组,key是开始索引以及结束索引,val是更新区间后的val,好处是节省空间。最后也是求前缀和,map已经把索引排序了,直接遍历map即可,等同于遍历diff数组。
这道题是之前那道 Meeting Rooms 的拓展,那道题只问我们是否能参加所有的会,也就是看会议之间有没有时间冲突,而这道题让求最少需要安排几个会议室,有时间冲突的肯定需要安排在不同的会议室。这道题有好几种解法,先来看使用TreeMap 来做的,遍历时间区间,对于起始时间,映射值自增1,对于结束时间,映射值自减1,然后定义结果变量 res,和房间数 rooms,遍历 TreeMap,时间从小到大,房间数每次加上映射值,然后更新结果 res,遇到起始时间,映射是正数,则房间数会增加,如果一个时间是一个会议的结束时间,也是另一个会议的开始时间,则映射值先减后加仍为0,并不用分配新的房间,而结束时间的映射值为负数更不会增加房间数,利用这种思路可以写出代码如下:
*/
class Solution1 {
public:
int minMeetingRooms(vector>& intervals) {
map m;
for (auto a : intervals) {
++m[a[0]];
--m[a[1]];
}
int rooms = 0, res = 0;
for (auto it : m) {
res = max(res, rooms += it.second);
}
return res;
}
}; /*
方法3:两个一维数组
第二种方法是用两个一维数组来做,分别保存起始时间和结束时间,然后各自排个序,定义结果变量 res 和结束时间指针 endpos,然后开始遍历,
如果当前起始时间小于结束时间指针的时间,则结果自增1,反之结束时间指针自增1,这样可以找出重叠的时间段,从而安排新的会议室,
参见代码如下:
*/
class Solution2 {
public:
int minMeetingRooms(vector>& intervals) {
vector starts, ends;
int res = 0, endpos = 0;
for (auto a : intervals) {
starts.push_back(a[0]);
ends.push_back(a[1]);
}
sort(starts.begin(), starts.end());
sort(ends.begin(), ends.end());
for (int i = 0; i < intervals.size(); ++i) {
if (starts[i] < ends[endpos]) ++res;
else ++endpos;
}
return res;
}
}; 题目:人数最多的时段
方法:差分数组。(可用diff vector数组(消耗内存可能很大),也可用map表消耗内存小)
思路:求最大值时的思路同会议室2那题。
解法1:用diff vector数组,当endtime很大时,要申请很大的内存。
// 方法: 差分 + stl + lamda
// 思路:先对区间做差分处理,对差分后的结果(求前缀和后的结果),用max_element找到最大值,用一遍遍历find_if、prev、distance求出区间。
class solution {
public:
vector> maxValRange(vector> &input)
{
vector> result;
// 求差分数组大小: stl + lamda
int maxEnd = (*max_element(input.begin(), input.end(), [](vector& in1, vector& in2){
return in1[1] < in2[1];
}))[1];
// 差分
vector diff(maxEnd + 1);
for (auto& ele : input) {
diff[ele[0]] += ele[2];
if (ele[1] + 1 < diff.size()) {
diff[ele[1] + 1] -= ele[2];
}
}
vector prefixSum(maxEnd + 1);
prefixSum[0] = diff[0];
for (int i = 1; i < diff.size(); i++) {
prefixSum[i] = prefixSum[i - 1] + diff[i];
}
// 对差分结果,找最大值,并一遍遍历找最大值连续区间. stl
int maxVal = *max_element(prefixSum.begin(), prefixSum.end());
auto it = find(prefixSum.begin(), prefixSum.end(), maxVal);
auto begin = prefixSum.begin();
auto end = prefixSum.end();
while (it != end) {
auto next = find_if(it, end, [&](int val) {
return val != maxVal;
});
if (next != end || (next == end && *prev(next) == maxVal)) {
result.push_back({distance(begin, it), distance(begin, prev(next))});
}
it = find(next, end, maxVal);;
}
return result;
}
}; 解法2:用map来标识差分数组
class Solution {
public:
vector> FindPeriods(const vector>& persons) {
int len = persons.size();
map diff; // 差分数组
// 记录差分数组
for (int i = 0; i < len; ++i) {
diff[persons[i][0]] += persons[i][2];
diff[persons[i][1] + 1] -= persons[i][2];
}
int peopleCnt = 0; // 当前的人数
int maxPeople = 0; // 最大的人数
for (auto it = diff.begin(); it != diff.end(); ++it) {
peopleCnt += it->second;
// 利用diff记录当前人数
it->second = peopleCnt;
// 刷新最大人数
maxPeople = max(maxPeople, peopleCnt);
}
vector> ans;
bool recordFlag = false;
for (auto it = diff.begin(); it != diff.end(); ++it) {
if (it->second == maxPeople) {
// 如果前一区间没有结束,不能插入新的区间
if (!recordFlag) {
ans.push_back(vector(2, it->first));
}
// 标记需要记录区间的结束时间
recordFlag = true;
} else if (recordFlag) {
recordFlag = false;
// 刷新区间的结束时间
ans[ans.size() - 1][1] = it->first - 1;
}
}
return ans;
}
};