数据结构：树的概念 | 二叉树的概念 | 根据前序和中序遍历构建二叉树 | 根据中序和后序遍历构建二叉树

一、树的概念

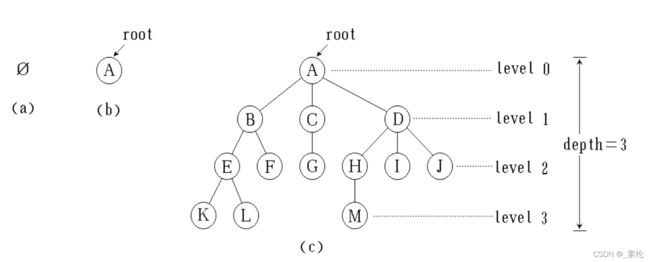
树是由n（n >= 0）个结点组成的有限集合，如果n = 0， 则称为空树，如果n > 0，则

1. 有一个特定的称之为根（root）的结点，它只有直接后继，没有直接前驱。
2. 除根以外的其他结点划分为m个互不相交的有限集合，每个集合又是一棵树，并且称之为根的子树（subtree），每棵子树的根结点有且仅有一个直接前驱，但可以有0个或多个直接后继。

1.名词解释

1. 节点的度：一个节点含有的子树的个数称为该节点的度；
2. 树的度：一棵树中，最大的节点的度称为树的度；
3. 叶节点或终端节点：度为零的节点；
4. 非终端节点或分支节点：度不为零的节点;
5. 父亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点;
6. 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点;
7. 兄弟节点：具有相同父节点的节点互称为兄弟节点;
8. 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推;
9. 深度：对于任意节点n，n的深度为从根到n的唯一路径长，根的深度为0;
10. 高度：对于任意节点n，n的高度为从n到一片树叶的最长路径长，所有树叶的高度为0;
11. 堂兄弟节点：父节点在同一层的节点互为堂兄弟;
12. 节点的祖先：从根到该节点所经分支上的所有节点;
13. 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
14. 森林：由m (m>=O)棵互不相交的树的集合称为森林;
15. 树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树。反之是有序树。

二、二叉树的概念

1. 二叉树的定义

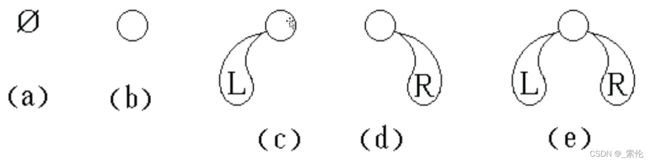
一棵二叉树是结点的一个有限集合，该集合或者为空，或者由一个根结点加上两棵称之为左子树和右子树的、两个互不相交的二叉树组成。

2. 二叉树的性质

1. 若二叉树的层次从0开始，则在二叉树的第 i 层最多有 2^i 个结点。(i>= 0)。
2. 高度为k的二叉树最多有2^(k+1) - 1个结点。(k >= -1)[证明用求等比级数前k项和的公式]。
3. 对任何一棵二叉树，如果其叶结点个数为n0，度为2的非叶结点个数为n2，则有n0 = n2 + 1。
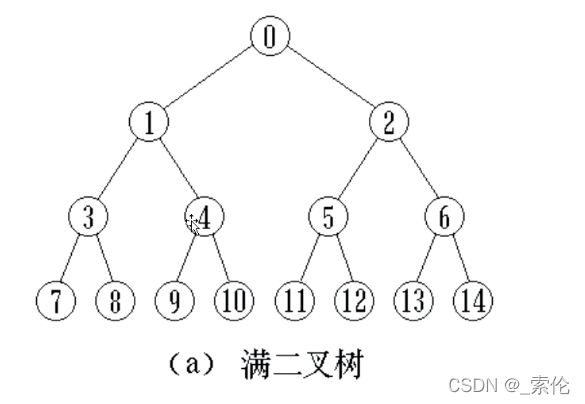
4. 定义：满二叉树(Full Binary Tree)：每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。

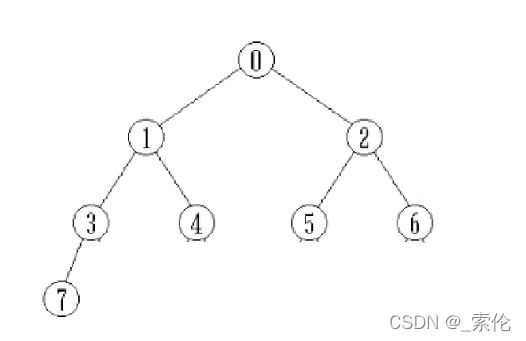
5. 定义：完全二叉树(Complete Binary Tree)：若设二叉树的高度为h，则共有h+1层。除第h层外，其它各层(0 ～h-1) 的结点数都达到最大个数，第h层从右向左连续缺若干结点，这就是完全二叉树。

3.二叉树的存储表示

数据元素之间的关系有两种不同的表示方法：顺序映象和非顺序映象，并由此得到两种不同的存储结构：顺序存储结构和链式存储结构。

数据的存储结构是指数据的逻辑结构在计算机中的表示。

3.1 顺序存储表示

这种表示形式，结点直接有一种关系：

1. 如果得知一个结点的编号为 i ，那如果它有左子树，那么左子树编号为(2 * i + 1)， 存在右子树的话，右子树编号为(2 * i + 2)。
2. 如果得知一个结点编号为 j ，那么其双亲结点编号为(j - 1) / 2;
   

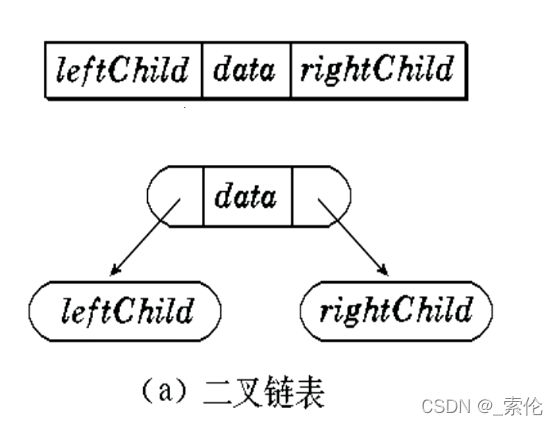
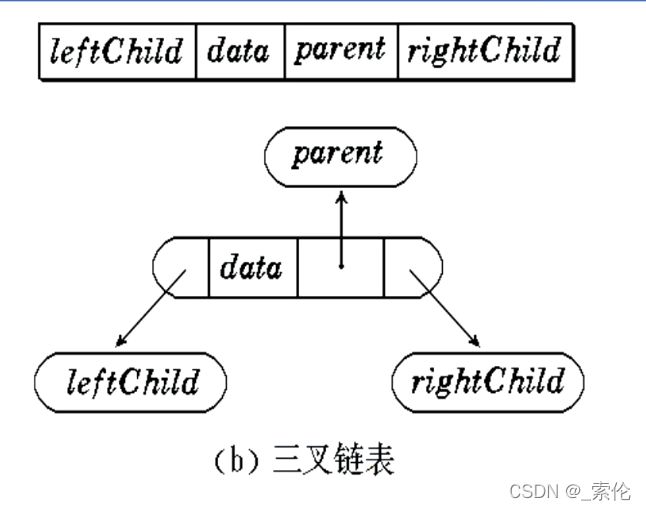
3.2 链式表示：二叉树链表表示

下图分别是二叉树的树型逻辑图，二叉链表表示图，三叉链表表示图

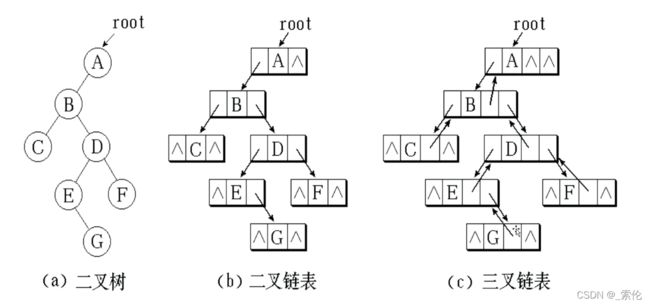
4.链式二叉树的设计

二叉链表方式，没有parent的二叉树

typedef int ElemType;
typedef struct BtNode
{
	ElemType data;
	struct BtNode* leftchild;
	struct BtNode* rightchild;
}BtNode, *BinaryTree;

5. 二叉树的遍历

所谓树的遍历，就是按某种次序访问树中的结点，要求每个结点访问一次且仅访问一次。
设访问根结点记作V； 遍历根的左子树记作L；遍历根的右子树记作 R；

遍历规则	遍历方式
前序遍历（先序遍历）	VLR
中序遍历	LVR
后序遍历	LRV

1. 前序遍历规则：(Preorder Traversal)
   若二叉树为空，则结束;
   否则
   访问根结点(V);
   前序遍历左子树(L);
   前序遍历右子树( R )。

void PreOrder(BtNode* root)
{
	if (root != NULL)
	{
		cout << root->data << " ";
		PreOrder(root->leftchild);
		PreOrder(root->rightchild);
	}
}

2. 中序遍历规则:(Inorder Traversal)
   若二叉树为空，则结束;
   否则
   中序遍历左子树(L);
   访问根结点(V);
   中序遍历右子树( R )。

void InOrder(BtNode* root)
{
	if (root != NULL)
	{
		InOrder(root->leftchild);
		cout << root->data << " ";
		InOrder(root->rightchild);
	}
}

3. 后序遍历规则:(Postorder Traversal)
   若二叉树为空，则结束;
   否则
   后序遍历左子树(L);
   后序遍历右子树®;
   访问根结点(V)。

void PastOrder(BtNode* root)
{
	if (root != NULL)
	{
		PastOrder(root->leftchild);
		PastOrder(root->rightchild);
		cout << root->data << " ";
	}
}

6.二叉树的构建

6.1普通构建法

BtNode* Buynode()
{
	BtNode* s = (BtNode*)malloc(sizeof(BtNode));
	if (NULL == s) exit(1);
	memset(s, 0, sizeof(BtNode));
	return s;
}

 // ABC##DE##F##G#H##
BtNode* CBTree1()
{
	BtNode* s = NULL;
	ElemType elem;
	cin >> elem;
	if (elem != '#')
	{
		s = Buynode();
		s->data = elem;
		s->leftchild = CBTree1();
		s->rightchild = CBTree1();
	}
	return s;
}

6.2 根据先序遍历和中序遍历构建二叉树

这个过程实际上也是运用了分治策略，不停的划分，直至规模达到最小。

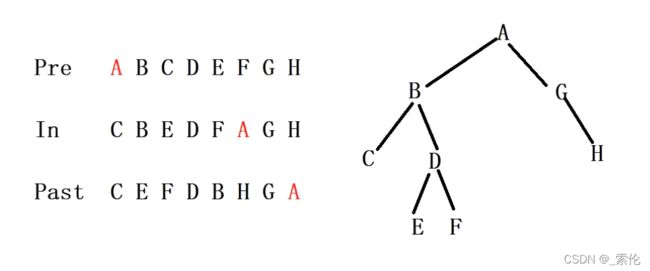
图解：

1. 树的逻辑图示，需要在已知先序和中序遍历结果情况下构建

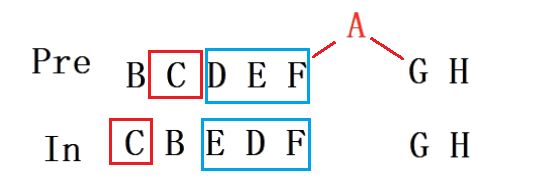
2. 通过中序遍历确定出先序遍历第一个元素的位置，那么中序遍历中A的左边就是A的左子树，有五个元素，所以先序遍历也要划分出五个元素作为左子树；剩下的G/H 为右子树。
   

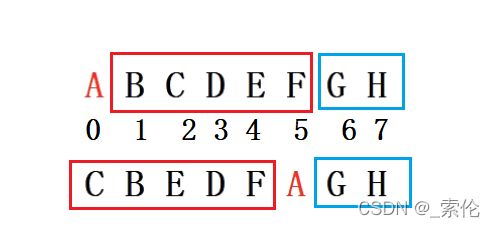
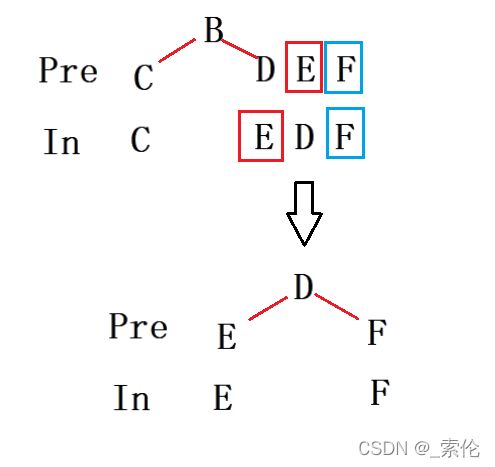
3. 在划分出左子树后，拿左子树继续划分，从中序遍历中找到先序遍历的元素B的位置，那么左边就是B的左子树，按照元素个数，先序遍历B的右边划分出相同元素个数作为左子树，剩下的作为右子树。

4. 继续划分，直至规模达到最小。

整体划分流程为：

代码

int FindIs(const char* is, int n, char ch)
{
	int pos = -1;
	for (int i = 0; i < n; ++i)
	{
		if (is[i] == ch)
		{
			pos = i;
			break;
		}
	}
	return pos;
}

BtNode* CreatePI(const char* ps, const char* is, int n)
{
	BtNode* s = NULL;
	if (n > 0)
	{
		s = Buynode();
		s->data = ps[0];
		int pos = FindIs(is, n, ps[0]);
		if (pos == -1) exit(1);

		s->leftchild = CreatePI(ps + 1, is, pos);
		s->rightchild = CreatePI(ps + 1 + pos, is + 1 + pos, n - pos - 1);
	}
	return s;
}

BtNode* CreateBinaryTreePI(const char* ps, const char* is, int n)
{
	if (ps == NULL || is == NULL || n < 0) return NULL;
	else
		return CreatePI(ps, is, n);
}

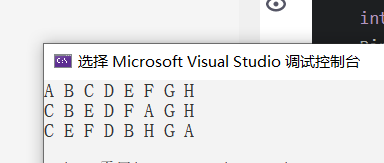
测试用例：

int main(void)
{
	char ps[] = { "ABCDEFGH" };
	char is[] = { "CBEDFAGH" };
	char ls[] = { "CEFDBHGA" };
	int n = strlen(ps);
	BinaryTree root = NULL;
	root = CreateBinaryTreePI(ps, is, n);

	PreOrder(root);
	cout << endl;
	InOrder(root);
	cout << endl;
	PastOrder(root);
	cout << endl;
	return 0;
}

6.3根据中序和后序遍历构建二叉树

和上述规则一样，分治策略划分

int FindIs(const char* is, int n, char ch)
{
	int pos = -1;
	for (int i = 0; i < n; ++i)
	{
		if (is[i] == ch)
		{
			pos = i;
			break;
		}
	}
	return pos;
}

BtNode* CreateIL(const char* is, const char* ls, int n)
{
	BtNode* s = NULL;
	if (n > 0)
	{
		s = Buynode();
		s->data = ls[n - 1];
		int pos = FindIs(is, n, ls[n - 1]);
		if (-1 == pos) exit(1);

		s->leftchild = CreateIL(is, ls, pos);
		s->rightchild = CreateIL(is + pos + 1, ls + pos, n - pos - 1);
	}
	return s;
}

BtNode* CreateBinaryTreeIL(const char* is, const char* ls, int n)
{
	if (is == NULL || ls == NULL || n <= 0) return NULL;
	else
		return CreateIL(is, ls, n);
}

测试用例：

int main(void)
{
	char ps[] = { "ABCDEFGH" };
	char is[] = { "CBEDFAGH" };
	char ls[] = { "CEFDBHGA" };
	int n = strlen(ps);
	BinaryTree root = NULL;
	root = CreateBinaryTreeIL(is, ls, n);

	PreOrder(root);
	cout << endl;
	InOrder(root);
	cout << endl;
	PastOrder(root);
	cout << endl;
	return 0;
}