二叉树各种遍历功能的实现（c/c++）

目录

一、预备定义

1.自定义数据结构

2.关于栈和队列的自定义函数

栈：

队列：

二、根据完整先序序列，递归创建二叉树（二叉链表存储结构）

三、各种遍历

1.递归方式先序遍历

2.递归方式中序遍历

3.递归方式后序遍历

4.非递归方式前序遍历

5.非递归方式中序遍历

6.非递归方式后序遍历

7.层次遍历

8.递归销毁二叉树

四、功能菜单和主函数

---

一、预备定义

1.自定义数据结构

二叉树结点、循环顺序队列、数据栈结点、数据栈、指针栈结点，指针栈。

#define _CRT_SECURE_NO_WARNINGS  //去警告提示
#include 
#include 

#define QUEUE_MAX_LENGTH 20  //最多存19个元素

// 二叉树结点的定义
typedef struct _BiNode
{
    char data;
    struct _BiNode* lchild;
    struct _BiNode* rchild;
}BiNode, * BiTree;        

// 固定长度的循序顺序队列结构体
typedef struct
{
    BiTree data[QUEUE_MAX_LENGTH];
    int front;  //指向队头元素的前一个元素
    int rear;  //指向队尾元素
} SeqQueue;


// 数据栈结点结构体  （非递归后序遍历时使用）
typedef struct DataNode
{
    char data;  // 数据域为char类型
    struct DataNode* next;
} DataStackNode;

// 数据栈结构体
typedef struct
{
    DataStackNode* top;  // 指向数据栈结点
} DataLinkedStack;


// 指针栈结点结构体
typedef struct PtrNode
{
    BiTree data;  // 数据域为BiTree类型
    struct PtrNode* next;
} PtrStackNode;

// 指针栈结构体
typedef struct
{
    PtrStackNode* top;  // 指向指针栈结点
} PtrLinkedStack;

2.关于栈和队列的自定义函数

初始化数据栈、进数据栈、出数据栈、判断数据栈是否为空。

初始化指针栈、进指针栈、出指针栈、判断指针栈是否为空、获取指针栈栈顶。

初始化队列、判断队列是否为空、判断队列是否为满、获取当前队列中有多少个元素、进队、出队、读取队头和队尾。

栈：

// 数据栈初始化为空栈
void initDataStack(DataLinkedStack& stack)
{
    stack.top = NULL;
}

/* 进栈一个元素 */
void pushDataStack(DataLinkedStack& stack, char e)
{
    DataStackNode* p;

    // 开辟空间，构造结点
    p = (DataStackNode*)malloc(sizeof(DataStackNode));
    p->data = e;
    p->next = NULL;

    // 入栈
    p->next = stack.top;
    stack.top = p;
}


/* 出栈一个元素 */
int popFromDataStack(DataLinkedStack& S, char& e)
{
    DataStackNode* p;  //出栈不需要为其开辟空间

    if (NULL != S.top)
    {
        p = S.top;
        S.top = p->next;

        e = p->data;
        free(p);

        return 1;        // 出栈成功
    }
    else
        return 0;        // 栈为空，出栈失败
}

/* 判断数据栈是否为空 */
int isEmptyDataStack(DataLinkedStack S)
{
    if (NULL == S.top)
        return 1;        // 栈为空，则返回1
    else
        return 0;        // 否则， 返回0
}


//

// 指针栈初始化为空栈
void initPtrStack(PtrLinkedStack& stack)
{
    stack.top = NULL;
}


/* 判断指针栈是否为空 */
int isEmptyPtrStack(PtrLinkedStack stack)
{
    if (NULL == stack.top)
        return 1;        // 栈为空，则返回1
    else
        return 0;        // 否则， 返回0
}

/* 进栈一个元素 */
void pushToPtrStack(PtrLinkedStack& stack, BiTree e)
{
    PtrStackNode* p;

    // 开辟空间，构造结点
    p = (PtrStackNode*)malloc(sizeof(PtrStackNode));
    p->data = e;
    p->next = NULL;

    // 入栈
    p->next = stack.top;
    stack.top = p;
}

/* 出栈一个元素 */
int popFromPtrStack(PtrLinkedStack& stack, BiTree& e)
{
    PtrStackNode* p;

    if (NULL != stack.top)
    {
        p = stack.top;
        stack.top = p->next;
        // 或stack.top = stack.top->next;

        e = p->data;
        free(p);

        return 1;        // 出栈成功
    }
    else
        return 0;        // 栈为空，出栈失败
}

/* 获取栈顶 */
int getTopOfPtrStack(PtrLinkedStack stack, BiTree& e)
{
    if (NULL != stack.top)
    {
        e = stack.top->data;
        return 1;        // 栈不为空，获取栈顶成功，则返回1
    }
    else
        return 0;        // 否则， 返回0
}

队列：

// 初始化为空队列
// 队头和队尾指向顺序队列数组中的最后一个元素
void initQueue(SeqQueue& queue)
{
    queue.front = queue.rear = QUEUE_MAX_LENGTH - 1;
}


// 判断队列是否为满
// 队尾指针下一个指向队头时队满
int queueIsFull(SeqQueue queue)
{
    if (queue.front == (queue.rear + 1) % QUEUE_MAX_LENGTH)
        return 1;
    else
        return 0;
}

// 判断队列是否为空
// 队头队尾指向同一元素时队列为空
int queueIsEmpty(SeqQueue queue)
{
    if (queue.front == queue.rear)
        return 1;
    else
        return 0;
}


/* 进队一个元素 */
int inQueue(SeqQueue& queue, BiTree e)
{
    if (1 == queueIsFull(queue))
        return 0;            // 队列已满，无法进队
    else
    {
        queue.rear = (queue.rear + 1) % QUEUE_MAX_LENGTH;
        queue.data[queue.rear] = e;

        return 1;            // 进队成功
    }
}


/* 出队一个元素 */
int outQueue(SeqQueue& queue, BiTree& e)
{
    if (1 == queueIsEmpty(queue))
        return 0;            // 队列已空，无法出队
    else
    {
        queue.front = (queue.front + 1) % QUEUE_MAX_LENGTH;  
        e = queue.data[queue.front];

        return 1;            // 出队成功（实际元素仍存在于数组中，逻辑上出队成功）
    }
}


// 获取当前队列中有多少个元素
int getElemNum(SeqQueue queue)
{
    return (queue.rear - queue.front + QUEUE_MAX_LENGTH) % QUEUE_MAX_LENGTH;
}

/* 读取队头和队尾元素的信息 */
int getFrontRear(SeqQueue queue, BiTree& ef, BiTree& er)
{
    if (1 == queueIsEmpty(queue))
        return 0;            // 队列已空，无队头和队尾
    else
    {
        ef = queue.data[queue.front + 1];
        er = queue.data[queue.rear];

        return 1;
    }
}

二、根据完整先序序列，递归创建二叉树（二叉链表存储结构）

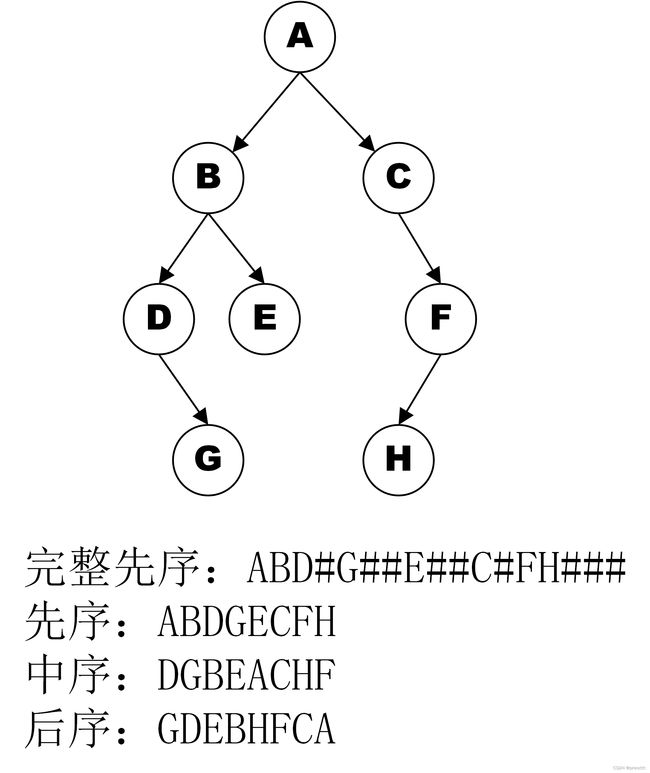
BT.dat 文件内容（完整先序序列）：ABD#G##E##C#FH###

递归算法（图文详解）_碎涛的博客-CSDN博客_递归算法

个人易错点：每次递归“归来”时都要从开始递归的代码行，继续执行后续代码，直到进行下一次“归来”，而不是忽略后续代码的执行直接继续下一次“归来”。

BiNode* createBiTree(FILE* fp)
{
    char ch;
    BiNode* p;

    // 从文件中依次读取各个结点值（空树为#）
    ch = fgetc(fp);

    if ('#' != ch)
    {
        // 开辟空间，构造结点，最后递归创建左右子树
        p = (BiNode*)malloc(sizeof(BiNode));
        p->data = ch;

        // 递归创建ch结点的左子树
        p->lchild = createBiTree(fp);

        // 递归创建ch结点的右子树
        p->rchild = createBiTree(fp);

        return p;  //返回根节点地址
    }
    else
        return NULL;
}

三、各种遍历

1.递归方式先序遍历

void preOrder(BiTree root)
{
    if (root == NULL) {  // 特殊情况优先考虑
        return;
    }
    printf("%2c", root->data);
    preOrder(root->lchild);
    preOrder(root->rchild);
}

2.递归方式中序遍历

void inOrder(BiTree root)
{
    if (root == NULL) {
        return;
    }
    inOrder(root->lchild);
    printf("%2c", root->data);
    inOrder(root->rchild);

}

3.递归方式后序遍历

void postOrder(BiTree root)
{
    if (root == NULL) {
        return;
    }
    postOrder(root->lchild);
    postOrder(root->rchild);
    printf("%2c", root->data);
}

4.非递归方式前序遍历

利用栈。

先将根结点输出，然后将其右孩子进指针栈、左孩子进指针栈，先右后左进栈则先左后右出栈。

当指针栈不为空时，出栈一个元素，对其进行先序遍历：先将根结点输出，然后将根结点的右、左孩子依次进栈。

void nonRecursionPreOrder(BiTree root)
{
    PtrLinkedStack ptrStack;
    BiTree subRoot = NULL;

    // 先将栈初始化为空
    initPtrStack(ptrStack);

    // 先序遍历时，根应最先访问，所以先将根结点输出
    printf("%2c", root->data);
 

    // 再将右子树和左子树根结点的地址，依次进指针栈ptrStack  
    //先右后左进栈，先左后右出栈
    if (NULL != root->rchild)
        pushToPtrStack(ptrStack, root->rchild);

    if (NULL != root->lchild)
        pushToPtrStack(ptrStack, root->lchild);

    // 当PLStack栈不为空时，说明还有子树没有遍历
    while (0 == isEmptyPtrStack(ptrStack))
    {
        // 出栈一个元素（某棵子树根结点的地址） （左）
        popFromPtrStack(ptrStack, subRoot);

        // 先将根结点的值输出
        printf("%2c", subRoot->data);
      

        // 再将右子树和左子树根结点的地址，依次进指针栈ptrStack
        if (NULL != subRoot->rchild)
            pushToPtrStack(ptrStack, subRoot->rchild);

        if (NULL != subRoot->lchild)
            pushToPtrStack(ptrStack, subRoot->lchild);
    }
}

5.非递归方式中序遍历

（1）根结点先进栈。

（2）当栈不为空时，出栈一个元素：

        若为叶子结点则直接输出；

        若不是叶子结点，判断其第几次出栈：看栈顶是否为自己的右孩子，若是则为第二次出栈，若不是则为第一次出栈。对于没有右孩子的结点，进栈时将根节点多进一次栈，此时若为第二次出栈则其右孩子为自己。

                第一次出栈，代表以自己为根的子树，将其分解为三部分，并按 “右根左”的顺序进栈。

                第二次出栈：代表自己，可直接输出。 

void nonRecursionInOrder(BiTree root)
{
    PtrLinkedStack ptrStack;        // 定义一个结点指针型栈
    BiTree outElem, topElem;    // 分别用来保存出栈元素和栈顶元素

    // 先将指针栈初始化为空
    initPtrStack(ptrStack);

    // 二叉树的根进栈
    if (NULL != root)
        pushToPtrStack(ptrStack, root);

    // 当PLStack栈不为空时，说明还有子树没有遍历
    while (0 == isEmptyPtrStack(ptrStack))
    {
        // 出栈一个元素（某棵子树根结点的地址）
        popFromPtrStack(ptrStack, outElem);

        // 如果出栈的是叶子结点，则直接输出；
        if (NULL == outElem->lchild && NULL == outElem->rchild)
            printf("%2c", outElem->data);
        else
        {
            // 如果出栈的结点不是叶子
            if (1 == getTopOfPtrStack(ptrStack, topElem))  //判断是否成功获取栈顶
            {
                // 出栈时栈顶为其右孩子则说明其第二次出栈，代表自己出栈，可直接输出（孩子在栈里说明自己已被拆分进栈过一次）
                if (outElem->rchild == topElem) {
                    printf("%2c", outElem->data);
                }
                else if (topElem == outElem) {     // 栈顶等于自己，说明出栈结点无右孩子，当前栈顶是多进栈的
                    printf("%2c", outElem->data);
                    popFromPtrStack(ptrStack, outElem);  //扔掉重复进栈的根，因为该结点是因为当前结点无右孩子而多进栈的
                }
                else
                {
                    if (NULL != outElem->rchild)
                        pushToPtrStack(ptrStack, outElem->rchild);        // 右子树的根进栈
                    else
                    {
                        //对于没有右孩子的，虚构一个等于自己的右孩子（进两次栈），这样当栈顶为自己则表示第二次出栈
                        pushToPtrStack(ptrStack, outElem);
                    }

                    pushToPtrStack(ptrStack, outElem);                // 二叉树的根进栈

                    if (NULL != outElem->lchild)
                        pushToPtrStack(ptrStack, outElem->lchild);        // 左子树的根进栈   
                }
            }
            // 若获取栈顶失败，出栈元素必须分解为三部分，并按“右根左”的顺序进栈。
            else 
            {
                if (NULL != outElem->rchild)
                    pushToPtrStack(ptrStack, outElem->rchild);        // 右子树的根进栈
                else
                {
                    //对于没有右孩子的，虚构一个等于自己的右孩子（进两次栈），若栈顶为自己则表示第二次出栈
                    pushToPtrStack(ptrStack, outElem);
                }

                pushToPtrStack(ptrStack, outElem);                // 二叉树的根进栈

                if (NULL != outElem->lchild)
                    pushToPtrStack(ptrStack, outElem->lchild);        // 左子树的根进栈   
            }

        }
            
            
    }
    
}


/*    下面这个函数，也可以进行非递归中序遍历，
    但是在遍历过程中，二叉链表将被破坏，所以一般不用这种方法！*/
    // 会破坏二叉链表存储结构的非递归方式中序遍历
void problematicNonRecursionInOrder(BiTree root)
{
    PtrLinkedStack ptrStack;    // 定义一个结点指针型栈
    BiTree leftChild;

    // 先将栈初始化为空
    initPtrStack(ptrStack);

    // 二叉树的根进栈
    if (NULL != root)
        pushToPtrStack(ptrStack, root);

    // 当PLStack栈不为空时，说明还有子树没有遍历
    while (0 == isEmptyPtrStack(ptrStack))
    {
        BiTree p = NULL;

        // 出栈一个元素（某棵子树根结点的地址）
        popFromPtrStack(ptrStack, p);

        // 如果该根结点的左右子树都不存在（即为孤立结点），则直接输出；
        // 否则，必须分解为三部分按“右根左”的顺序进栈。
        // 注意：根结点也作为一个单独的子树，所以其左右指针域应先设置为NULL。
        if (NULL == p->lchild && NULL == p->rchild)
        {
            printf("%2c", p->data);
        }
        else
        {
            leftChild = p->lchild;                    // 先保留左子树根的地址

            if (NULL != p->rchild)
                pushToPtrStack(ptrStack, p->rchild);    // 右子树的根进栈

            p->lchild = NULL;                 //清空左右孩子域，进去孤立结点
            p->rchild = NULL;
            pushToPtrStack(ptrStack, p);                // 二叉树的根进栈

            if (NULL != leftChild)
                pushToPtrStack(ptrStack, leftChild);    // 左子树的根进栈
        }
    }
}

6.非递归方式后序遍历

设置指针栈和数据栈。数据栈数据域为char，指针栈数据域为BiTree。

进栈：

        数据栈：根→根右→根左

        指针栈：（栈底）根的左子树→根的右子树

                当指针栈不为空时，说明还有子树没有遍历：出栈，将其根进数据栈，将其左右子树依次进指针栈。

将数据栈元素出栈，即可得到后序遍历序列。

// Function5--非递归方式后序遍历
void nonRecursionPostOrder(BiTree root)
{
    DataLinkedStack dataStack;        // 定义一个输出数据栈
    PtrLinkedStack ptrStack;            // 定义一个结点指针型栈

    // 先将两个栈都初始化为空
    initDataStack(dataStack);
    initPtrStack(ptrStack);

    // 后序遍历时，根应最后访问，所以先将根结点的值进数据栈DLStack
    pushDataStack(dataStack, root->data);

    // 再将左子树和右子树根结点的地址，依次进指针栈PLStack  
    if (NULL != root->lchild)
        pushToPtrStack(ptrStack, root->lchild);

    if (NULL != root->rchild)
        pushToPtrStack(ptrStack, root->rchild);  

    // 当PLStack栈不为空时，说明还有子树没有遍历
    while (0 == isEmptyPtrStack(ptrStack))
    {
        BiTree pNode = NULL;

        // 出栈一个元素（某棵子树根结点的地址）
        popFromPtrStack(ptrStack, pNode);

        // 先将根结点的值进数据栈DLStack
        pushDataStack(dataStack, pNode->data);

        // 再将左子树和右子树根结点的地址，依次进指针栈PLStack
        if (NULL != pNode->lchild)
            pushToPtrStack(ptrStack, pNode->lchild);

        if (NULL != pNode->rchild)
            pushToPtrStack(ptrStack, pNode->rchild);
    }

    // 数据栈dataStack依次出栈，即可得到后序遍历序列
    while (0 == isEmptyDataStack(dataStack))
    {
        char value = ' ';

        // 出栈一个元素（某结点的值），并输出
        popFromDataStack(dataStack, value);
        printf("%2c", value);
    }
}

7.层次遍历

void hierarchicalOrder(BiTree root)
{
    BiTree pNode = NULL;
    SeqQueue queue;

    // 初始化为空队列
    initQueue(queue);

    // 树根结点的地址先进队
    inQueue(queue, root);

    // 只要队列不为空，则一直循环
    while (queueIsEmpty(queue) == 0) {
        outQueue(queue, pNode);
        printf("%2c", pNode->data);

        if (pNode->lchild != NULL)
            inQueue(queue, pNode->lchild);
        if (pNode->rchild != NULL)
            inQueue(queue, pNode->rchild);

    }


}

8.递归销毁二叉树

void destroy(BiTree root)
{
    if (NULL != root)
    {
        if (NULL != root->lchild)        // 左子树不为空，则递归销毁左子树
            destroy(root->lchild);

        if (NULL != root->rchild)        // 右子树不为空，则递归销毁右子树
            destroy(root->rchild);

        printf("%c node has been freed!\n", root->data);
        free(root);        // 最后直接释放根结点
    }
}

四、功能菜单和主函数

// 功能菜单
void menu()
{
    printf("\n\t************************Binary Linked List************************\n");
    printf("\t*    1--Read data from a file to create a binary tree            *\n");
    printf("\t*    2--PreOrder, InOrder and PostOrder traversal by recursion   *\n");
    printf("\t*    3--PreOrder traversal by non-recursion                      *\n");
    printf("\t*    4--InOrder traversal by non-recursion                       *\n");
    printf("\t*    5--PostOrder traversal by non-recursion                     *\n");
    printf("\t*    6--Hierarchical traversal (using queue)                     *\n");
    printf("\t*    7--Destroy the entire binary tree                           *\n");
    printf("\t*    8--Clear screen                                             *\n");
    printf("\t*    0--Exit program                                             *\n");
    printf("\t******************************************************************\n");
    printf("\tPlease select a menu item:");
}

int main()
{
    int choice;
    char c;
    BiTree root = NULL;        
    FILE* fpFrom;

    system("chcp 65001");  // 设置window控制台（CMD或命令行窗口）为UTF-8格式

    while (1)
    {
        menu();
        scanf("%d", &choice);

        switch (choice)
        {
        case 1:
            if (NULL != root)
            {
                printf("The current binary tree is not empty, please destroy it before rebuild!\n");
            }
            else
            {
                // 因为createBiTree()函数递归时要不断从文件中读取字符，所以先打开文件
                // 如果在createBiTree()函数中每读一个字符，就打开并关闭文件一次，则效率太低
                fpFrom = fopen("BT.dat", "r");
                if (NULL == fpFrom)
                {
                    printf("File containing complete PreOrdered sequence cannot be opened, binary tree creation failed!\n");
                    break;
                }

                root = createBiTree(fpFrom);

                fclose(fpFrom);
                printf("Binary tree created successfully!\n");
            }
            break;

        case 2:
            if (NULL != root)
            {
                printf("The PreOrdered sequence is as follows:");
                preOrder(root);

                printf("\nThe InOrdered sequence is as follows:");
                inOrder(root);

                printf("\nThe PostOrdered sequence is as follows:");
                postOrder(root);

                printf("\n");
            }
            else
                printf("The current binary tree is empty, please create the binary tree first!\n");
            break;

        case 3:
            if (NULL != root)
            {
                printf("The non-recursive PreOrdered sequence is as follows:\n");
                nonRecursionPreOrder(root);
                printf("\n");
            }
            else
                printf("The current binary tree is empty, please create the binary tree first!\n");
            break;

        case 4:
            if (NULL != root)
            {
                printf("The non-recursive InOrdered sequence is as follows:\n");
                nonRecursionInOrder(root);
                printf("\n");
            }
            else
                printf("The current binary tree is empty, please create the binary tree first!\n");
            break;

        case 5:
            if (NULL != root)
            {
                printf("The non-recursive PostOrder sequence is as follows:\n");
                nonRecursionPostOrder(root);
                printf("\n");
            }
            else
                printf("The current binary tree is empty, please create the binary tree first!\n");
            break;

        case 6:
            if (NULL != root)
            {
                printf("The hierarchical ordered sequence is as follows:\n");
                hierarchicalOrder(root);
                printf("\n");
            }
            else
                printf("The current binary tree is empty, please create the binary tree first!\n");
            break;

        case 7:
            if (NULL != root)
            {
                destroy(root);
                root = NULL;
                printf("The binary tree destroyed successfully!\n");
            }
            else
                printf("The current binary tree is empty, no need to destroy!\n");
            break;

        case 8:
            system("cls");
            break;

        case 0:
            // 关闭保存结果的文件后，再退出程序
            exit(0);
            break;

        default:
            // If the user enters an alphabetic menu item instead of an integer, 
            // the buffer needs to be emptied
            while ((c = getchar()) != '\n' && c != EOF);
            printf("The menu item you entered does not exist, please select it again!\n");
        }
    }
    return 0;
}

五、代码实现

测试数据：ABD#G##E##C#FH###

（放在文件"BT.dat"中）

 （二进制文件要与源程序.cpp放在一个文件夹下）

我实现了一下是没问题的。

说明：本文代码是我的数据结构作业，是老师写的，因为理解不透彻所以自己写了注释和分析，发现要自己写还是有点困难qwq，好歹自己理了一下思路，希望对你们有帮助.OvO.