下一个排列(next_permutation)
目录
1.next_permutation函数的作用
2.next_permutation函数的原理与设计
3.代码实现
next_permutation函数的作用
next_permutation函数是头文件
其返回值是 bool ,传入值为 迭代器
但是今天我们将不会严格按照原版next_permutation设计,我会用数组代替动态数组容器 vector,以及返回值设计为void;
next_permutation函数的原理与设计
前提知识:字典序
若知晓字典序可以跳过这段示例讲解。
其实字典序不难理解,或者我早就使用过它,例如在排序字符串时。
字典序(dictionary order),又称 字母序(alphabetical order),原意是表示英文单词在字典中的先后顺序,在计算机领域中扩展成两个任意字符串的大小关系。
例如字符串“abcd\0”,"abcdef\0"以及"af\0"之间的字典序大小
在第二字母时,'f'最晚出现所以"af\0"是最大的。而在第五个字母时,'e'比'\0'晚出现,所以"abcdef\0"第二大;
说完这些,我可以来看看全排列;
例如1,2,3的全排列有[1,2,3]、[1,3,2]、[2,1,3]、[2,3,1]、[3,1,2]、[3,2,1]。
我们可以发现,所谓的下一个排列无非就是字典稍大一点的,
翻译成数学语言:
记P(n)是第n个排列的字典序大小,那么P(n)的下一个排列必定满足;
存在一个Ni,当 Ni <= i 时,都有 P(n)< P(i),且 对于Ni满足P(N)<= P(Ni),那么P(N)就是P(n)的下一个全排列;
说人话就是,在比当前排列字典序大的排列中,字典序最小的就是当前排列的下一个全排列;
例如比[1,2,3]大的有[1,3,2]、[2,1,3]、[2,3,1]、[3,1,2]、[3,2,1],而其中[1,3,2]最小;
接下来就是讲解实现的数学原理与逻辑。
首先我们明确一个重中之重的要点:我需要想方设法构造出 比当前全排列字典序稍大一点的全排列;
那么有一个朴素的想法就是大的元素一点前移就好。
我们一定知道一个条件,一个排列最小字典序一定时升序排列的,最大字典序是降序排列的
也就是,当前部区间相同时,让后续区间中的元素尽可能满足降序。
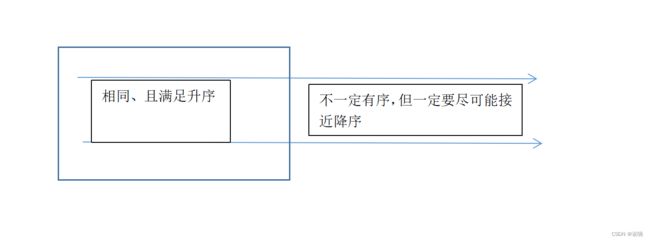
如果,我们数轴上表示两个排列大小,因为我们从小生成大序列,那么前面总有一段区间满足升序(注意区间长度可以为0)
而后半部分不一定有序,因为一旦后部分完全是降序排列的,那么说明已经抵达了在保证前区间相同时的最大值。下文称为 局部最大值。
当处于局部最大值时,我们需要让前半部分的升序区间长度-1。或者说让需要降序排列区间长度+1
图1.结构化图(全局)
图2.尾部必然会有区间满足
如何让排列尽可能趋向、抵达局部最大值呢?
我们来思考一下,因为前半部分相同,那必然不会对字典序产生影响,所以我们需要考虑后续部分的变化;单独拿出后续区间的排列,因此我们获得了一个新排列,接下来思考新排列的情况。
而后续部分中一定也有图1的情况。我们在抛弃前半部分,因为我们无需关心这部分;
如此这般,最后尾部一定会有一段部分满足图2情况(区间长度可以为0);
而关键是 尾部一定会产生一个局部最大值。既然一定会产生这种情况,那我们一定要对其进行做出改变;
怎么改变?之前我们说过了,减少升序区间的长度就好了;
这就简单了,我们需要做以下几件事情:
1.标记出升序部分的尾部 i
2.在降序序列中寻找比它稍大一点的元素
3.交换这两个元素
//哦!这还没完
4.需要将 i+1 到 整个数组尾部的元素升序
代码实现
void reverse(int* begin, int* end) {
int n = end - begin;
for (int i = 0; i < n / 2; ++i) {
int temp = begin[i];
begin[i] = end[- i - 1];
end[- i - 1] = temp;
}
}
void nextPermutation(int* nums, int n) {
int i = n - 2;
while (i >= 0 && nums[i] >= nums[i + 1]) {
i--;
}
if (i >= 0) {
int j = n - 1;
while (j >= 0 && nums[i] >= nums[j]) {
j--;
}
int temp = nums[j];
nums[j] = nums[i];
nums[i] = temp;
}
reverse(nums + i + 1, nums + n);
}