NeuDs 数据结构 树&二叉树

一.判断题

二叉树只能用二叉链表表示。F

在含有n个结点的树中，边数只能是n-1条。T

一棵有124个结点的完全二叉树，其叶结点个数是确定的。F

树形结构中元素之间存在一个对多个的关系。F

用树的前序遍历和中序遍历可以导出树的后序遍历。F

此结论只适用于二叉树

完全二叉树中，若一个结点没有左孩子，则它必是树叶。T

(2条消息) 完全二叉树中，若一个结点没有左孩子，则它必是树叶_Rookie_聪的博客-CSDN博客

某二叉树的前序和中序遍历序列正好一样，则该二叉树中的任何结点一定都无右孩子。F

[解析]前序:root,L,R中序:L,root,R.那就无左孩子

度为二的树就是二叉树。F 

二叉树是度数最大为2的树，不是度数就是2的树，可能二叉树只有一个子树或者没有子树，那么这时二叉树度数为1或者0 度数为2的树：树的所有节点的度都小于等于2，且至少有一个节点的度为2。 二叉树：树的所有节点都必须小于等于2。 

某二叉树的后序和中序遍历序列正好一样，则该二叉树中的任何结点一定都无右孩子。T 

二叉树通常有顺序存储结构和链式存储结构。T

一棵有n个结点的二叉树，从上至下，从左到右用自然数依次编号，则编号为i的结点的左儿子的编号为2i(2i

 

一棵有n个结点的二叉树,按层次从上到下,同一层从左到右顺序存__牛客网 (nowcoder.com) 

二.选择题 

1.以下说法错误的是 ( )

A.线性结构中的一个结点至多只有一个直接后继

B.树形结构的特点是一个结点可以有多个直接前趋

C.树形结构可以表达(组织)更复杂的数据

D.任何只含一个结点的集合是一棵树

E.树(及一切树形结构)是一种"分支层次"结构

2.中序遍历图示二叉树的结果为 ：

A.     A，B，D，H，I，E，C，F，G

B.     A，B，C，D，H，E，I，F，G

C.     H，I，D，B，E，F，G，A，C

D.     H，D，I，B，E，A，F，C，G

 3.一棵二叉树中有7个度为2的结点和5个度为1的结点，其总共有（ ）个结点。

A.18

B.20

C.16

D.30

 

4.完全二叉树的叶子结点数

一棵有 1001 个结点的完全二叉树，其叶子结点数为 ▁▁▁▁▁ 。

A.500

B.250

C.254

D.501

(3条消息) 一棵完全二叉树，结点总数为1001，求它的叶子结点总数，度为2的结点总数，有多少个结点只有非空左子树，有多少个结点只有非空右子树？_非空左子树和非空右子树怎么求_于储的博客-CSDN博客

5.由3 个结点可以构造出多少种不同的二叉树( )

A.5

B.4

C.2

D.3

6.二叉树的先序序列和中序序列相同的条件是（ ）。

A.右子树为空

B.任何结点至多只有左子女的二叉树

C.左子树为空

D.任何结点至多只有右子女的二叉树

7.下面的函数PreOrderPrintLeaves(BinTree BT)按前序遍历的顺序打印出二叉树BT的所有叶子结点。则下列哪条表达式应被填在空中？

void PreOrderPrintLeaves( BinTree BT )
{  if (BT)  {
      if (___________________)  printf("  %d", BT->Data);
      PreOrderPrintLeaves( BT->Left  );
      PreOrderPrintLeaves( BT->Right );
   }
}

 A.!BT->Left

B.!BT->Right

C.BT->Data != 0

D.!(BT->Left || BT->Right)

8.深度为6的二叉树最多有( )个结点。 

A.63

B.32

C.64

D.31

二叉树的性质：高度(深度)为h的二叉树至多有2^h-1个结点（h≥1） 

9. 假设一棵二叉树的结点个数为50，则它的最小高度是（　）。

A.4

B.5

C.6

D.7

如果是满二叉树 2^k-1=50 k=6 表示层数为6但第六层未满

答案应该是C。高度最少的时候，就是除了叶子结点外，其他的每层都是满节点，即满二叉树。满二叉数节点和高度的关系有：节点数=2的高度次方-1，由此可以推算出，当节点数是50的时候，该二叉树的最小高度是6层，故选c。

10.已知某二叉树的后序遍历序列是dabec, 中序遍历序列是debac , 它的前序遍历是（ ）。

A.deabc

B.acbed

C.decab

D.cedba

11.度为3的树中第4层上至多有（ ）个结点。

A.81

B.12

C.8

D.27

12.如果二叉树的前序遍历结果是12345，后序遍历结果是32541，那么该二叉树的中序遍历结果是什么？

A.23154

B.24135

C.无法确定

D.23145

13.若一棵二叉树具有10个度为2的结点，5个度为1的结点，则度为0的结点个数是（ ）个。

A.不确定

B.9

C.11

D.15

二叉树的性质：度为 0 的节点数等于度为 2 的节点数 + 1

总结点数=n0+n1+n2 

14.一个具有1025个结点的二叉树的高h为（ ）个。

A.11至1025之间

B.10

C.11

D.10至1024之间

A 因为每层一个结点时二叉树的层次为最大,此时为1025层,即高度为1025
而二叉树为完全二叉树时其层次最小,2^10 - 1 < 1025 < 2^11 - 1 ,所以为完全二叉树时其层次为11层,即最小高度为11,最大高度为1025,所以选A

15.在下列存储形式中，（ ）不是树的存储形式。

A.双亲表示法

B.顺序存储表示法

C.孩子兄弟表示法

D.孩子链表表示法

题干为树（不是二叉树）的存储形式，有3中常用的存储结构：①双亲表示法；②孩子表示法；③孩子兄弟表示法 

16.在二叉树的二叉链表结构中，指针p所指结点为叶子结点的条件是（ ）。

A.p->rchlid==NULL

B.p->lchild==NULL && p->rchlid==NULL

C.p->lchild==NULL

D.p=NULL

17.

A.g

B.a

C.c

D.f

18.树最适合于用来表示()

A.有序数据元素

B.无序数据元素

C.元素之间无联系的数据

D.元素之间具有分支层次关系的数据

19.用二叉链表表示具有n个结点的二叉树时，值为空的指针域的个数为( )

A.n-1

B.n+l

C.2n

D.n

由n=n0+n1+n2,n0=n2+1,得n=n1+2n2+1;

因为二叉树，所以n1为0或1；

1）当n1为0时，n2=(n-1)/2,空指针：2n-2*(n-1)/2=n+1;

2)  当n1为1时，n2=(n-2)/2,空指针：2n-2*(n-2)/2-1=n+1.

20.具有9个叶结点的二叉树中有____个度为2的结点。()

A.8

B.11

C.9

D.10

二叉树当中;n0=n2+1 

三.编程题

1.

R6-1 求二叉树高度

分数 15

全屏浏览题目

切换布局

作者 陈越

单位 浙江大学

本题要求给定二叉树的高度。

函数接口定义：

int GetHeight( BinTree BT );

其中BinTree结构定义如下：

typedef struct TNode *Position; typedef Position BinTree; struct TNode{ ElementType Data; BinTree Left; BinTree Right; }; 

要求函数返回给定二叉树BT的高度值。

裁判测试程序样例：

#include  #include  typedef char ElementType; typedef struct TNode *Position; typedef Position BinTree; struct TNode{ ElementType Data; BinTree Left; BinTree Right; }; BinTree CreatBinTree(); /* 实现细节忽略 */ int GetHeight( BinTree BT ); int main() { BinTree BT = CreatBinTree(); printf("%d\n", GetHeight(BT)); return 0; } /* 你的代码将被嵌在这里 */ 

输出样例（对于图中给出的树）：

4

int GetHeight( BinTree BT )
{
    if (!BT) return 0; // 空树高度为0
    int leftHeight = GetHeight(BT->Left); // 左子树高度
    int rightHeight = GetHeight(BT->Right); // 右子树高度
    return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1; // 返回左右子树高度的最大值加1
}

R6-2 先序输出叶结点

分数 15

全屏浏览题目

切换布局

作者 陈越

单位 浙江大学

本题要求按照先序遍历的顺序输出给定二叉树的叶结点。

函数接口定义：

void PreorderPrintLeaves( BinTree BT ); 

其中BinTree结构定义如下：

typedef struct TNode *Position; typedef Position BinTree; struct TNode{ ElementType Data; BinTree Left; BinTree Right; }; 

函数PreorderPrintLeaves应按照先序遍历的顺序输出给定二叉树BT的叶结点，格式为一个空格跟着一个字符。

裁判测试程序样例：

#include  #include  typedef char ElementType; typedef struct TNode *Position; typedef Position BinTree; struct TNode{ ElementType Data; BinTree Left; BinTree Right; }; BinTree CreatBinTree(); /* 实现细节忽略 */ void PreorderPrintLeaves( BinTree BT ); int main() { BinTree BT = CreatBinTree(); printf("Leaf nodes are:"); PreorderPrintLeaves(BT); printf("\n"); return 0; } /* 你的代码将被嵌在这里 */ 

输出样例（对于图中给出的树）：

Leaf nodes are: D E H I

//先序遍历二叉树，遇到叶子结点输出
void PreorderPrintLeaves( BinTree BT )
{
    if(BT) //如果当前结点不为空
    {
        if(!BT->Left && !BT->Right) //如果当前结点是叶子结点
            printf(" %c", BT->Data); //输出该结点的数据
        PreorderPrintLeaves(BT->Left); //递归遍历左子树
        PreorderPrintLeaves(BT->Right); //递归遍历右子树
    }
}

R6-3 中序输出度为1的结点

分数 15

全屏浏览题目

切换布局

作者 DS课程组

单位 临沂大学

本题要求实现一个函数，按照中序遍历的顺序输出给定二叉树中度为1的结点。

函数接口定义：

void InorderPrintNodes( BiTree T); 

T是二叉树树根指针，InorderPrintNodes按照中序遍历的顺序输出给定二叉树T中度为1的结点，格式为一个空格跟着一个字符。

其中BiTree结构定义如下：

typedef struct BiTNode
{
    ElemType data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

裁判测试程序样例：

#include  #include  typedef char ElemType; typedef struct BiTNode { ElemType data; struct BiTNode *lchild,*rchild; }BiTNode,*BiTree; BiTree Create();/* 细节在此不表 */ void InorderPrintNodes( BiTree T); int main() { BiTree T = Create(); printf("Nodes are:"); InorderPrintNodes(T); return 0; } /* 你的代码将被嵌在这里 */ 

输入样例：

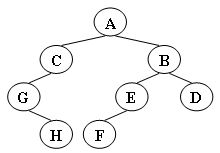
输入为由字母和'#'组成的字符串，代表二叉树的扩展先序序列。例如对于如下二叉树，输入数据：

ACG#H###BEF###D##

输出样例（对于图中给出的树）：

Nodes are: G C E

void InorderPrintNodes(BiTree T) {
    if (T == NULL) return;
    InorderPrintNodes(T->lchild);
    if ((T->lchild == NULL && T->rchild != NULL) || (T->lchild != NULL && T->rchild == NULL)) {
        printf(" %c", T->data);
    }
    InorderPrintNodes(T->rchild);
}